人教版八年级上册12.2 三角形全等的判定课后练习题

这是一份人教版八年级上册12.2 三角形全等的判定课后练习题，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
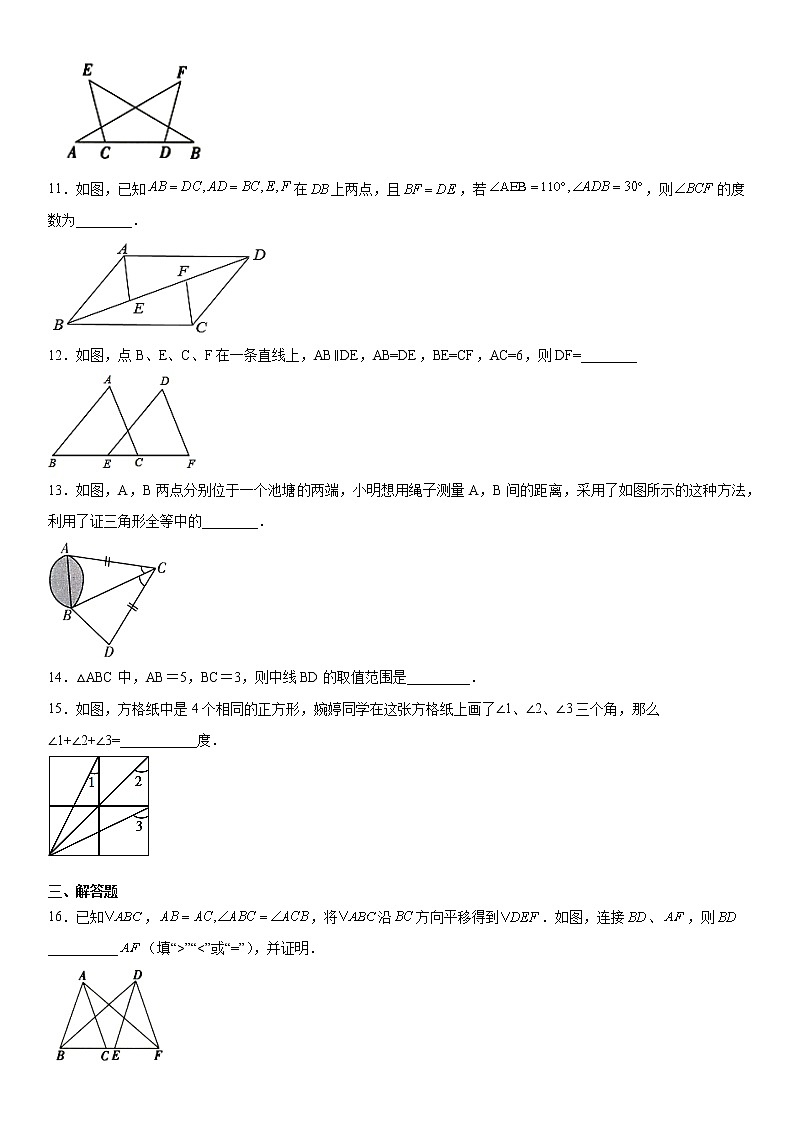
八年级人教版数学第十二章12.2.2《全等三角形的判定--边角边”SAS“》同步测试-2021-2022学年秋季学校:___________姓名：___________班级：___________考号：___________一、选择题1．如图，把长短确定的两根木棍AB、AC的一端固定在A处，和第三根木棍BM摆出△ABC，木棍AB固定，木棍AC绕A转动，得到△ABD，这个实验说明（　　）A．△ABC与△ABD不全等B．有两边分别相等的两个三角形不一定全等C．两边和它们的夹角分别相等的两个三角形全等D．有两边和其中一边的对角分别相等的两个三角形不一定全等2．如图，已知：AC＝DF，AC∥FD，AE＝DB，判断△ABC≌△DEF的依据是（　　）A．SSS B．SAS C．ASA D．AAS3．如图，点B、E、C、F在同一条直线上，，，要用SAS证明≌，可以添加的条件是　　A． B． C． D．4．如图，在△ABC与△EMN中，，，∠C=∠M=54°，若∠A=66°，则下列结论正确的是(        )A． B．EN=a C．∠E=60° D．∠N=66°5．如图，两车从南北方向的路段的端出发，分别向东、向西行进相同的距离到达两地，若与的距离为千米，则与的距离为（    ）A．千米 B．千米 C．千米 D．无法确定6．如图，在△ABC和△DEF中，AB＝DE，ABDE，运用“SAS”判定△ABC≌△DEF，需补充的条件是（　　）A．AC＝DF B．∠A＝∠D C．BE＝CF D．∠ACB＝∠DFE7．．如图，梯形ABCD中，AD∥BC，点M是AD的中点，且MB=MC，若AD=4，AB=6，BC=8，则梯形ABCD的周长为（　　）A．22 B．24 C．26 D．288．如图，由∠1=∠2，BC=DC，AC=EC，得△ABC≌△EDC的根据是（    ）A．SAS B．ASA C．AAS D．SSS  二、填空题9．如图，把两根钢条AA′、BB′的中点连在一起，可以做成一个测量内槽宽的工具（卡钳），若测得A′B′=8厘米，则工件内槽AB宽为______厘米．10．如图，已知，经分析____________________，依据是__________．11．如图，已知在上两点，且，若，则的度数为________．12．如图，点B、E、C、F在一条直线上，AB∥DE，AB=DE，BE=CF，AC=6，则DF=________13．如图，A，B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，采用了如图所示的这种方法，利用了证三角形全等中的________．14．△ABC中，AB＝5，BC＝3，则中线BD的取值范围是_________．15．如图，方格纸中是4个相同的正方形，婉婷同学在这张方格纸上画了∠1、∠2、∠3三个角，那么∠1+∠2+∠3=___________度． 三、解答题16．已知，，将沿方向平移得到．如图，连接、，则__________（填“>”“<”或“=”），并证明．17．如图，已知在中，求证：．    18．已知：如图，，E是的中点，，求证：（1）；（2）．     19．如图，在五边形中，．（1）求证：；（时，）（2）当时，求的度数．（五边形的内角和是）   20．已知，点D为直线上一动点（点D不与点B、C重合），，，，，，连接．（1）如图1，当点D在线段上时，求证：①，②；（2）如图2，当点D在线段的延长线上时，其他条件不变，请直接写出三条线段之间的关系．
参考答案1．D【分析】根据全等三角形的判定方法即可判断；【详解】由题意可知：AB＝AB，AC＝AD，∠ABC＝∠ABD，满足有两边和其中一边的对角分别相等，但是△ABC与△ABD不全等，故选：D．【点睛】本题考查全等三角形的判定，记住有两边和其中一边的对角分别相等的两个三角形不一定全等．2．B【分析】根据两直线平行内错角相等，再根据即可证明．【详解】解：，∴，，，，在△ABC和△DEF中 ，故选．【点睛】本题主要考查了全等三角形的判定，关键是根据两直线平行内错角相等解答．3．C【分析】根据AB∥DE得出∠B=∠DEF，添加条件BC=EF，则利用SAS定理证明△ABC≌△DEF．【详解】解：∵AB∥DE，
∴∠B=∠DEF，
可添加条件BC=EF，
理由：∵在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS）；
故选C．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等时，必需有边的条件，若有两边一角对应相等时，角必需是两边的夹角．4．A【分析】利用，，∠C=∠M=54°证明与全等，利用全等三角形的性质可得到答案．【详解】解：在与中， 所以： 所以B，C，D，都错误，A正确．故选A．【点睛】本题考查三角形全等的判定，掌握三角形全等的判定方法是关键．5．A【分析】先由条件证明，再根据全等三角形的性质即可得出结论．【详解】解：由题意得：AC=AD，， ∴在和中 ∴∴∴与的距离为千米故选：A．【点睛】本题全等三角形的应用，读懂图信息，将文字语言转化为几何语言是解题关键．6．C【分析】证出∠ABC＝∠DEF，由SAS即可得出结论．【详解】解：补充BE＝CF，理由如下：∵AB∥DE，∴∠ABC＝∠DEF，若要利用SAS判定，B、D选项不符合要求，若A：AC=DF，构成的是SSA，不能证明三角形全等，A选项不符合要求，C选项：BE=CF，∵BE＝CF，∴BC＝EF，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS），故选：C．【点睛】此题主要考查全等三角形的判定，解题的关键是熟知“SAS”的判定的特点．7．B【解析】先判断△AMB≌△DMC，从而得出AB=DC，然后代入数据即可求出梯形ABCD的周长．解：∵AD∥BC，∴∠AMB=∠MBC，∠DMC=∠MCB，又∵MC=MB，∴∠MBC=∠MCB，∴∠AMB=∠DMC，在△AMB和△DMC中，∵AM=DM，MB=MC，∠AMB=∠DMC∴△AMB≌△DMC，∴AB=DC，四边形ABCD的周长=AB+BC+CD+AD=24．故选B．8．A【详解】试题分析：∵∠1=∠2，∴∠ACD+∠2=∠ACD+∠1，即∠ACB=∠ECD．又∵BC=DC，AC=EC，∴△ABC≌△EDC（SAS）．故选A．考点：全等三角形的判定．9．8【分析】连接A′B′，可判定△AOB≌△A′OB′，根据全等三角形的性质可得AB=A′B′=8厘米．【详解】解：连接A′B′，∵两根钢条AA′、BB′的中点连在一起，∴OA=OA′，OB=OB′，在△AOB和△A′OB′中，，∴△AOB≌△A′OB′（SAS）．∴AB=A′B′=8厘米，故答案为8．【点睛】本题考查全等三角形的应用．在实际生活中，对于难以实地测量的线段，常常通过两个全等三角形，转化需要测量的线段到易测量的边上或者已知边上来，从而求解．10．            【分析】利用SAS得出全等三角形.【详解】证明：∵AC＝BD，∴AD＝BC，在△ADF和△BCE中∵ ，∴△ADF≌△BCE（SAS）.故答案为：①，②，③.【点睛】此题主要考查了全等三角形的判定，熟练掌握判定方法是解题的关键11．80【分析】先证明四边形ABCD是平行四边形，再通过条件证明,最后根据全等三角形的性质及三角形外角性质即可得出答案．【详解】∵，∴四边形ABCD是平行四边形，∴，在△AED和△CFB中，，∴，∴，∵，∴，故答案是．【点睛】本题主要考查了平行四边形的性质，结合外角定理计算是解题的关键．12．6.【分析】根据题中条件由SAS可得△ABC≌△DEF，根据全等三角形的性质可得AC=DF=6．【详解】∵AB∥DE，∴∠B=∠DEF∵BE=CF，∴BC=EF，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS），∴AC=DF=6．考点：全等三角形的判定与性质．13．SAS【分析】根据题意找到条件，利用全等三角形的判定方法确定正确的选项即可．【详解】观察图形发现：，，，所以利用了证三角形全等中的SAS（或边角边）．故答案为：SAS．【点睛】本题考查了全等三角形的判定方法，掌握方法是解答本题的关键，难度不大．14．1＜BD＜4【详解】延长BD到E，使BD=DE，连接AE，如图：∵BD是△ABC中线，∴AD=DC，在△BDC和△EDA中，∵，∴△BDC≌△EDA.∴BC=AE=3，∵在△ABE中，根据三角形的三边关系定理得：5+3＞BE＞5-3，∴2＜2BD＜8，即1＜BD＜4.故答案为1＜BD＜4.15．135【解析】由题意可知△ABC≌△EDC，∴∠3=∠BAC，又∵∠1+∠BAC=90°，∴∠1+∠3=90°，∵DF=DC，∴∠2=45°，∴∠1+∠2+∠3=135度，故答案为135.16．，证明见解析【分析】由沿方向平移得到，得到，，即可证明；【详解】解：．证明：由沿方向平移得到， 得，．在和中，，∴，∴．故答案是=．【点睛】本题主要考查了全等三角形的判定和性质，准确分析证明是解题的关键．17．见解析【分析】利用SAS证明，得到，即可求解．【详解】证明：在和中，∴．∴．又∵，即，∴，∴．【点睛】此题考查了全等三角形的证明与性质，熟练掌握全等三角形的判定方法与性质是解题的关键．18．（1）见解析；（2）见解析【分析】（1）根据∠ECD＝∠EDC，再利用平行线的性质进行证明即可；（2）根据SAS证明△AEC与△BED全等，再利用全等三角形的性质证明即可．【详解】证明：（1）∵，∴，∵，∴；（2）∵E是的中点，∴，在和中，∴，∴．【点睛】本题主要考查了全等三角形的判定以及全等三角形的性质，平行线的性质等知识，解题的关键是灵活运用准确寻找全等三角形解决问题，属于中考常考题型．19．（1）见解析；（2）80°【分析】（1）由题意易得，则有，然后问题可求证；（2）由题中所给五边形的内角和是可直接进行求解．【详解】解：（1）证明：∵，∴，又∵，∴，在和中，，∴；（2）解：∵，，∴，又∵，∴在五边形中，．【点睛】本题主要考查全等三角形的性质与判定，熟练掌握全等三角形的性质与判定是解题的关键．20．（1）①见解析；②见解析；（2）【分析】（1）①先得到，然后证明得到，从而得到；②由全等三角形的性质可以得到，则；（2）同（1）原理证明，得到，即可得到答案．【详解】解：（1）①证明：∵，∴，即，在和中，∴，∴，∴，∴，∴；②∵∴；（2）结论：，理由如下：∵，∴，即，在和中，∴，∴，∵，∴．