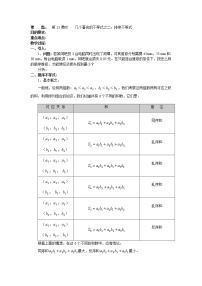
高中数学人教版新课标A选修4-5一 二维形式的柯西不等式教案

这是一份高中数学人教版新课标A选修4-5一 二维形式的柯西不等式教案，共5页。教案主要包含了课时安排，教学重点，教学难点，教学过程，二维柯西不等式的向量形式及应，板书设计，作业布置，教学反思等内容，欢迎下载使用。
一、教学目标1．认识柯西不等式的几种不同形式，理解其几何意义．2．通过运用柯西不等式分析解决一些简单问题．二、课时安排1课时三、教学重点认识柯西不等式的几种不同形式，理解其几何意义．四、教学难点通过运用柯西不等式分析解决一些简单问题．五、教学过程（一）导入新课复习基本不等式。（二）讲授新课教材整理　二维形式的柯西不等式内容等号成立的条件 代数形式若a，b，c，d都是实数，则(a2＋b2)·(c2＋d2)≥当且仅当        时，等号成立向量形式设α，β是两个向量，则|α·β|≤|α||β|当且仅当           ，或，等号成立三角形式设x1，y1，x2，y2∈R，那么＋≥ 当且仅当时，等号成立（三）重难点精讲题型一、二维柯西不等式的向量形式及应例1已知p，q均为正数，且p3＋q3＝2.求证：p＋q≤2.【精彩点拨】　为了利用柯西不等式的向量形式，可分别构造两个向量．【自主解答】　设m＝p，q，n＝(p，q)，则p2＋q2＝pp＋qq＝|m·n|≤|m||n|＝·＝.又∵(p＋q)2≤2(p2＋q2)，∴≤p2＋q2≤，∴≤·，则(p＋q)4≤8(p＋q)．又p＋q>0，∴(p＋q)3≤8，故p＋q≤2.规律总结：使用二维柯西不等式的向量形式证明不等式，关键是合理构造出两个向量．同时，要注意向量模的计算公式|a|＝对数学式子变形的影响．[再练一题]1．若本例的条件中，把“p3＋q3＝2”改为“p2＋q2＝2”，试判断结论是否仍然成立？【解】　设m＝(p，q)，n＝(1,1)，则p＋q＝p·1＋q·1＝|m·n|≤|m|·|n|＝·.又p2＋q2＝2.∴p＋q≤·＝2.故仍有结论p＋q≤2成立.题型二、运用柯西不等式求最值例2　若2x＋3y＝1，求4x2＋9y2的最小值．【精彩点拨】　由2x＋3y＝1以及4x2＋9y2的形式，联系柯西不等式，可以通过构造(12＋12)作为一个因式而解决问题．【自主解答】　由柯西不等式得(4x2＋9y2)(12＋12)≥(2x＋3y)2＝1.∴4x2＋9y2≥，当且仅当2x×1＝3y×1，即x＝，y＝时取等号．∴4x2＋9y2的最小值为.规律总结：1．利用柯西不等式求最值，不但要注意等号成立的条件，而且要善于配凑，保证出现常数结果．2．常用的配凑的技巧有：①巧拆常数；②重新安排某些项的次序；③适当添项；④适当改变结构，从而达到运用柯西不等式求最值的目的．[再练一题]2．若3x＋4y＝2，试求x2＋y2的最小值及最小值点.【解】　由柯西不等式(x2＋y2)(32＋42)≥(3x＋4y)2，得25(x2＋y2)≥4.所以x2＋y2≥，当且仅当＝时，“＝”成立．为求最小值点，需解方程组∴因此，当x＝，y＝时，x2＋y2取得最小值，最小值为，最小值点为.题型三、二维柯西不等式代数形式的应用例3已知|3x＋4y|＝5，求证：x2＋y2≥1.【精彩点拨】　探求已知条件与待证不等式之间的关系，设法构造柯西不等式进行证明．【自主解答】　由柯西不等式可知(x2＋y2)(32＋42)≥(3x＋4y)2，所以(x2＋y2)≥.又因为|3x＋4y|＝5，所以＝1，即x2＋y2≥1.规律总结：1．利用二维形式的柯西不等式证明时，要抓住柯西不等式的结构特征，必要时，需要将数学表达式适当变形．2．变形往往要求具有很高的技巧，必须善于分析题目的特征，根据题设条件，综合地利用添、拆、分解、组合、配方、变量代换、数形结合等方法才能发现问题的本质，找到突破口．[再练一题]3．设a，b∈R＋且a＋b＝2.求证：＋≥2.【证明】　根据柯西不等式，有[(2－a)＋(2－b)]＝[()2＋()2]＋≥＝(a＋b)2＝4.∴＋≥＝2，当且仅当·＝·，即a＝b＝1时等号成立．∴＋≥2.（四）归纳小结二维柯西不等式—（五）随堂检测1．设x，y∈R，且2x＋3y＝13，则x2＋y2的最小值为(　　)A.      B．169       C．13      D.0【解析】　(2x＋3y)2≤(22＋32)(x2＋y2)，∴x2＋y2≥13.【答案】　C2．已知a，b∈R＋，且a＋b＝1，则(＋)2的最大值是(　　)A．2        B.        C．6          D.12【解析】　(＋)2＝(1×＋1×)2≤(12＋12)(4a＋1＋4b＋1)＝2[4(a＋b)＋2]＝2×(4×1＋2)＝12，当且仅当＝，即a＝b＝时等号成立．故选D.【答案】　D3．平面向量a，b中，若a＝(4，－3)，|b|＝1，且a·b＝5，则向量b＝________.【解析】　|a|＝＝5，且 |b|＝1，∴a·b＝|a|·|b|，因此，b与a共线，且方向相同，∴b＝.【答案】　     六、板书设计3.1二维形式的柯西不等式 教材整理　二维形式的柯西不等式 例1：例2：例3： 学生板演练习七、作业布置同步练习：3.1二维形式的柯西不等式八、教学反思