数学八年级上册4 平行线的性质教学ppt课件

这是一份数学八年级上册4 平行线的性质教学ppt课件，共16页。PPT课件主要包含了例题讲解，课堂小结，两直线平行，同位角相等，内错角相等，同旁内角互补等内容，欢迎下载使用。

如图所示，工人在修一条高速公路时在前方遇到一座高山，为了降低施工难度，工程师决定绕过这座山，如果第一个弯是左拐30°，那么第二个弯应朝什么方向，才能不改变原来的方向？
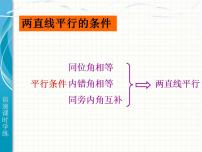
(1)公理：同位角相等，两直线平行；
(2)定理：内错角相等，两直线平行；
(3)定理：同旁内角互补，两直线平行.
(2)在平面内，如果两条直线都和第三条直线垂直，那么这两条直线平行 .
已知：如图所示，直线AB∥CD，∠1和∠2是直线AB，CD被直线EF截出的同位角。求证：∠1=∠2.
(1)∠1和∠2在数量关系上有哪两种情况?(2)过直线外一点有几条直线与这条直线平行?
证明：假设∠1 ≠ ∠2，过点M作直线GH，使∠EMH= ∠2，如图所示.根据“同位角相等，两直线平行”，可知GH ∥ CD.又因为AB ∥ CD，这样经过点M存在两条直线AB和GH都与直线CD平行.
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.这说明∠1 ≠ ∠2的假设不成立，所以∠1 =∠2.
根据同位角相等可以判定两直线平行，反过来，如果两直线平行，同位角之间有什么关系呢？内错角、同旁内角之间又有什么关系呢？1.两条平行直线被第三条直线所截，同位角是相等的，那么内错角、同旁内角之间有什么关系呢？
已知，如图，直线a∥b,∠1和∠2是直线a、b被直线c截出的内错角.求证：∠1=∠2.
证明：∵a∥b（已知）,∴∠3=∠2（两直线平行，同位角相等）.∵∠1=∠3（对顶角相等）,∴∠1=∠2（等量代换）.
两条平行直线被第三条直线所截,，内错角相等.
已知，如图，直线a∥b，∠1和∠2是直线a、b被直线c截出的同旁内角.求证：∠1+∠2=180°.
证明：∵a∥b（已知），∴∠3=∠2（两直线平行，同位角相等）。∵∠1+∠3=180°（1平角=180°），∴∠1+∠2=180°（等量代换）。
两直线平行，同旁内角互补.
两条直线被第三条直线所截.
已知：如图，直线a,b,c被直线d所截，且a∥b,c∥b，求证：a∥c.
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
(1)证明的一般步骤:①理解题意；②根据题意正确画出图形；③结合图形，写出“已知”和“求证”；④分析题意，探索证明的思路；⑤依据寻求的思路，运用数学符号和数学语言条理清晰地写出证明过程；⑥检查表达过程是否正确、完善.
完成一个定理的证明，需要哪些环节？
(2)证明的思路:①可以从求证出发向已知追溯，也可以由已知向结论探索，还可以从已知和结论两个方向同时出发，互相接近.②对于用文字叙述的命题的证明，要先分清命题的条件和结论，然后根据题意画出图形，写出已知和求证，证明即可.
如图所示，AB∥CD，∠CDE=140°，则∠A的度数为 (　　) A.140° B.60° C.50° D.40°
平行于同一直线的两条直线平行
1.平行线的性质定理有：　　 　　，　 　， 　 　　 　。
两直线平行,同位角相等
2.如图所示，∠4=∠C，∠1=∠2，求证BD平分∠ABC.
证明：∵∠4=∠C，∴AD∥BC，∴∠2=∠3.又∵∠1=∠2，∴∠1=∠3，即BD平分∠ABC.
两直线平行,内错角相等
两直线平行,同旁内角互补