北师大版九年级上册5 一元二次方程的根与系数的关系教课内容ppt课件

这是一份北师大版九年级上册5 一元二次方程的根与系数的关系教课内容ppt课件，共15页。PPT课件主要包含了学习目标，新课导入，合作探究，新课讲授，能得出以下结果，典例精析，随堂练习，x2-x-60等内容，欢迎下载使用。

1．掌握一元二次方程两根的和、两根的积与系数的关系．2．能根据根与系数的关系式和已知一个根的条件下，求出方程的另一根，以及方程中的未知系数．3．会利用根与系数的关系求关于两根代数式的值．
如何用判别式 b2 - 4ac 来判断一元二次方程根的情况？
对一元二次方程： ax2 + bx +c = 0(a≠0) b2 - 4ac > 0 时，方程有两个不相等的实数根.b2 - 4ac = 0 时，方程有两个相等的实数根.b2 - 4ac < 0 时，方程无实数根.
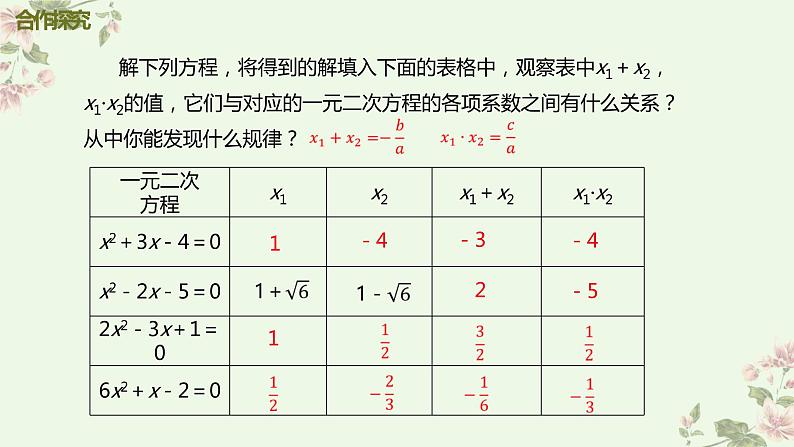
解下列方程，将得到的解填入下面的表格中，观察表中x1＋x2，x1·x2的值，它们与对应的一元二次方程的各项系数之间有什么关系？从中你能发现什么规律？
如何证明以上发现的规律呢？
证明：当Δ≥ 0 时，由求根公式得：
一般地，对于关于x的一元二次方程ax2＋bx＋c＝0(a≠0)，用求根公式求出它的两个根x1、x2，由一元二次方程ax2＋bx＋c＝0的求根公式知
例1、已知方程x2+mx+3=0的一个根是1，则它的另一个根是________，m的值是_______.
解：设方程的另一个根为x1,则x1·1=3，即x1=3,则-m=1+3,解得m=-4.
例3、已知关于x的方程x2-(k-1)x+k+1=0的两个实数根的平方和等于4，求实数k的值.
解：设方程的两个根为x1，x2，由根与系数的关系，得x1+x2=k-1，x1·x2=k+1.∵ x12+ x22 =4，即(x1+x2)2-2x1x2=4,∴(k-1)2-2(k+1)=4，即k2-4k-5=0，∴k=5或k=-1.当k=5时，b2-4ac=[-(k-1)]2-4(k+1)=-8<0，不符合题意，舍去；当k=-1时，b2-4ac=[-(k-1)]2-4(k+1)=4>0.∴k的值为-1.
1. 关于x的方程2x2+mx+n=0的两个根是-2和1，则nm的值为 (　　) A.-8　     B.8　     C.16　     D.-16
3. 已知关于x的一元二次方程x2-kx-4=0的一个根为2，则另一个根是 (　　) A.4　     B.1　     C.2　     D.-2
4. 以3、-2为根，且二次项系数为1的一元二次方程是______________.
6.已知关于x的一元二次方程x2-2(m+1)x+m2+2=0.(1)若方程有实数根，求实数m的取值范围;(2)若方程两实数根分别为x1、x2，且满足x12+ x22 =10，求实数m的值.
(2)∵方程x2-2(m+1)x+m2+2=0的两实数根分别为x1、x2，∴x1+x2=2(m+1)，x1·x2=m2+2，∴ x12+ x22 =(x1+x2)2-2x1·x2=[2(m+1)]2-2(m2+2)=2m2+8m=10，解得m1=-5(舍去)，m2=1，∴实数m的值为1.