






新教材2022届高考数学人教版一轮复习课件:3.2 单调性与最值
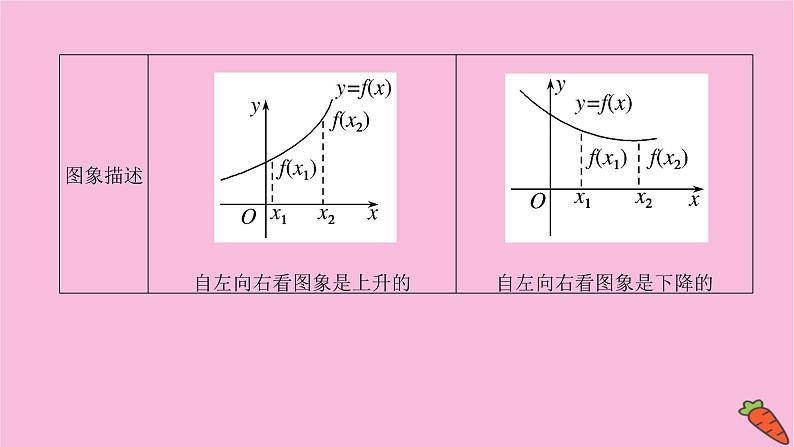
展开【教材回扣】1.函数的单调性(1)单调函数的定义
f(x1)
(2)单调区间的定义如果函数y=f(x)在区间D上是_________或_________,那么就说函数y=f(x)在这一区间具有(严格的)单调性,_________叫做y=f(x)的单调区间.
3.已知函数f(x)=4x2-kx-8在[5,20]上具有单调性,则实数k的取值范围是________.
2.若函数f(x)=x2+2(a-1)x+2的单调递减区间是(-∞,4],则实数a的值是________.
解析:因为函数f(x)的单调递减区间是(-∞,4],且函数f(x)的图象对称轴为直线x=1-a,所以有1-a=4,即a=-3.
题型一 函数的单调性角度1|求函数的单调区间[例1] (1)[2021·山东烟台模拟]函数f(x)=ln (x2-2x-8)的单调递增区间是( )A.(-∞,-2) B.(-∞,1)C.(1,+∞) D.(4,+∞)
解析:(1)由x2-2x-8>0,得f(x)的定义域为{x|x>4或x<-2}.设t=x2-2x-8,则y=ln t为增函数.要求函数f(x)的单调递增区间,即求函数t=x2-2x-8的单调递增区间(定义域内).∵函数t=x2-2x-8在(4,+∞)上单调递增,在(-∞,-2)上单调递减,∴函数f(x)的单调递增区间为(4,+∞).
答案: (2)[0,1)
类题通法求函数的单调区间,首先确定定义域,然后利用单调性的定义或借助图象求解即可.
类题通法解决此类问题除利用定义外,导数法是一种非常有效的方法,注意分类讨论思想的应用.
答案:(1)[-1,1)
答案:(1){y|y≠3}
类题通法比较函数值的大小,应将自变量转化到同一个单调区间内,然后利用函数的单调性解决.
角度2|解不等式[例5] 已知函数f(x)=ln x+2x,若f(x2-4)<2,则实数x的取值范围是________.
类题通法解此类问题,主要是利用函数的单调性将“f”符号脱掉,使其转化为具体的不等式求解.
答案:(1)(-∞,-3]
类题通法利用单调性求参数(1)视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数;(2)需注意若函数在区间[a,b]上是单调的,则该函数在此区间的任意子集区间上也是单调的.
[预测1] 核心素养——逻辑推理已知减函数f(x)的定义域是R,m,n都是实数,如果不等式f(m)-f(n)>f(-m)-f(-n)成立,那么下列不等式成立的是( )A.m-n<0 B.m-n>0C.m+n<0 D.m+n>0
解析:设F(x)=f(x)-f(-x),由于f(x)是R上的减函数,∴f(-x)是R上的增函数,-f(-x)是R上的减函数.∴F(x)是R上的减函数,∴当m
状 元 笔 记 求函数最值的常用方法一、配方法配方法是求二次型函数最值的基本方法,如y=a f 2(x)+bf(x)+c的函数的最值问题,可以考虑用配方法.
[典例1] 已知函数y=(ex-a)2+(e-x-a)2(a∈R,a≠0),求函数y的最小值.【思路】 将函数表达式按ex+e-x配方,转化为关于变量ex+e-x的二次函数.
【解析】 y=(ex-a)2+(e-x-a)2=(ex+e-x)2-2a(ex+e-x)+2a2-2.令t=ex+e-x,f(t)=t2-2at+2a2-2.∵t≥2,∴f(t)=t2-2at+2a2-2=(t-a)2+a2-2的定义域为[2,+∞).∵抛物线y=f(t)的对称轴为t=a,∴当a≤2且a≠0时,ymin=f(2)=2(a-1)2;当a>2时,ymin=f(a)=a2-2.综上,当a≤2且a≠0时,y的最小值为2(a-1)2;当a>2时,y的最小值为a2-2.
二、换元法换元法有两类,即代数换元和三角换元.如可用三角换元解决形如a2+b2=1及部分根式函数形式的最值问题.
三、不等式法主要是指运用基本不等式及其变形公式来解决函数最值问题的一种方法.
四、单调性法先确定函数在给定区间上的单调性,然后依据单调性求函数的最值.这种求解方法在高考中是必考的,且多在解答题的某一问中出现.
五、导数法设函数f(x)在区间[a,b]上连续,在区间(a,b)内可导,则f(x)在[a,b]上的最大值和最小值应为f(x)在(a,b)内的各极值与f(a),f(b)中的最大值和最小值,利用这种求函数最值的方法就是导数法.
[典例5] 函数f(x)=x3-12x+1在闭区间[-3,0]上的最大值、最小值分别是________.【思路】 先求闭区间上的函数的极值,再与端点函数值比较大小,确定最值.
【解析】 因为f ′(x)=3x2-12,所以令f ′(x)=0,得x=-2或x=2(舍去).又f(-3)=10,f(-2)=17,f(0)=1,比较得f(x)的最大值为17,最小值为1.
六、平方法对含根式的函数或含绝对值的函数,有的利用平方法,可以巧妙地将函数最值问题转化为我们熟知的、易于解决的函数最值问题.
【思路】 本题是无理函数的最值问题,可以先确定定义域,再两边平方,即可化为二次函数的最值问题,进而可以利用二次函数的最值解决.
七、数形结合法数形结合法,是指利用函数所表示的几何意义,借助几何方法及函数的图象求函数最值的一种常用的方法.
2025高考数学一轮复习-2.2-函数的单调性与最值【课件】: 这是一份2025高考数学一轮复习-2.2-函数的单调性与最值【课件】,共34页。PPT课件主要包含了课前双基巩固,课堂考点突破等内容,欢迎下载使用。
§2.2 函数的单调性与最值 课件-2025高考数学一轮复习: 这是一份§2.2 函数的单调性与最值 课件-2025高考数学一轮复习,共60页。PPT课件主要包含了落实主干知识,增函数或减函数,函数的最值,fx≤fx0,fx≥fx0,探究核心题型,方法二导数法,-11,课时精练,多项选择题等内容,欢迎下载使用。
新高考数学一轮复习讲练课件3.2 第1课时 导数与函数的单调性、极值与最值(含解析): 这是一份新高考数学一轮复习讲练课件3.2 第1课时 导数与函数的单调性、极值与最值(含解析),共21页。












