新教材2022届高考数学人教版一轮复习课件：8.1 基本立体图形及空间几何体的表面积和体积

这是一份新教材2022届高考数学人教版一轮复习课件：8.1 基本立体图形及空间几何体的表面积和体积，共59页。PPT课件主要包含了课前·基础巩固，平行且相等，平行四边形，三角形，旋转体的结构特征，πrl，πr＋r′l，S底h，πR2，课堂·题型讲解等内容，欢迎下载使用。
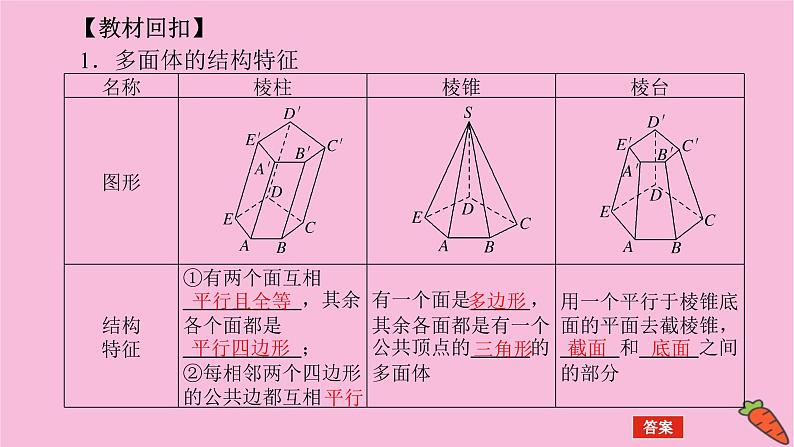
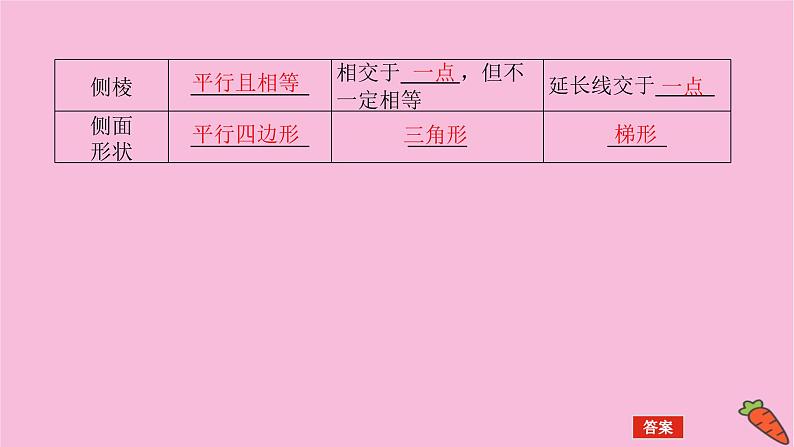
【教材回扣】1．多面体的结构特征
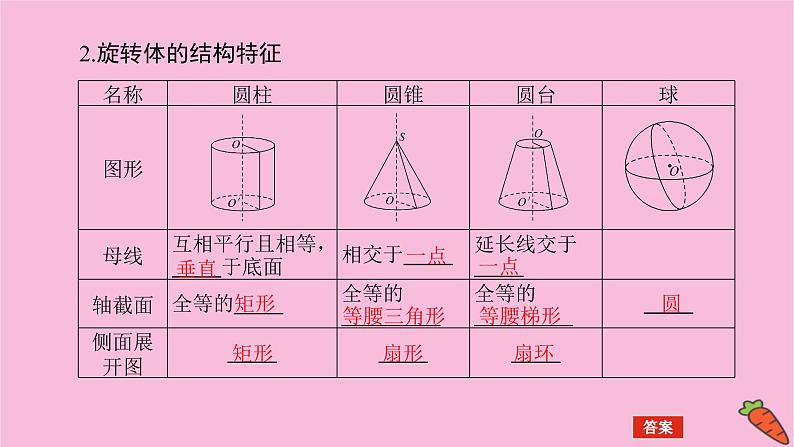
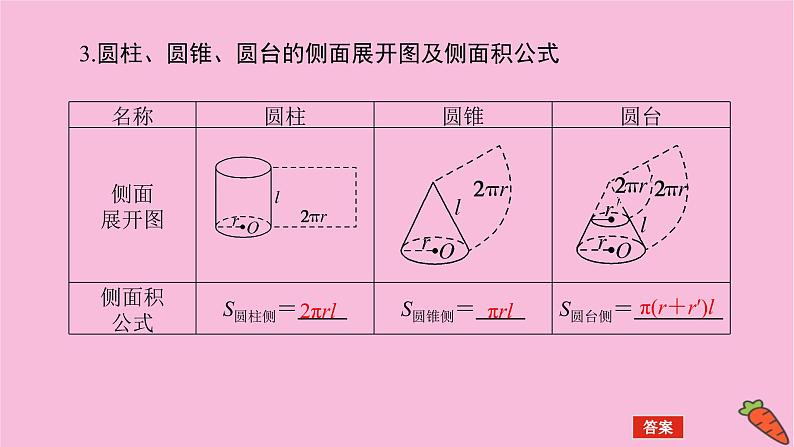
3.圆柱、圆锥、圆台的侧面展开图及侧面积公式
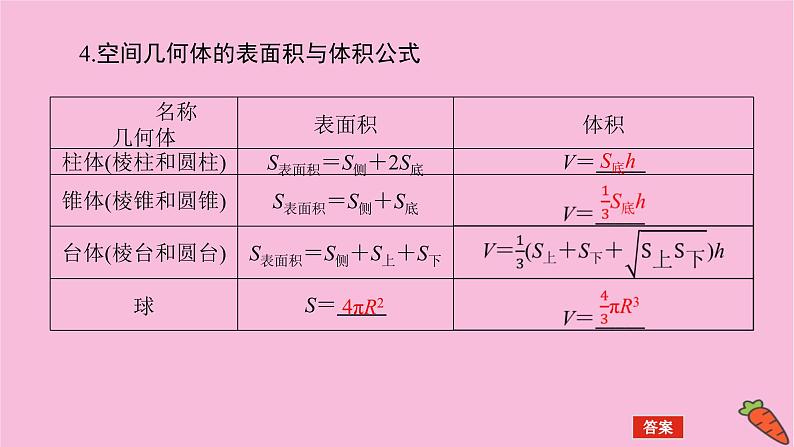
4.空间几何体的表面积与体积公式
【题组练透】题组一　判断正误(正确的打“√”，错误的打“×”)1．棱柱的侧棱都相等，侧面都是全等的平行四边形．( )2．有一个面是多边形，其余各面都是三角形的几何体是棱锥．( )3．棱台各侧棱的延长线交于一点．( )4．夹在圆柱的两个平行截面间的几何体还是旋转体．( )
题组二　教材改编1．(多选题)下面结论正确的是(　　)A．三角形的直观图是三角形B．平行四边形的直观图是平行四边形C．正方形的直观图是正方形D．菱形的直观图是菱形
解析：由斜二测直观图的画法法则可知，A、B正确，C不正确，因为正方形的直观图是平行四边形，D不正确，菱形的直观图不是菱形，而是平行四边形．故选AB.
3．如图，圆柱的底面直径和高都等于球的直径，则球与圆柱的体积之比为________．
题组三　易错自纠1．如图，长方体ABCD－A′B′C′D′中被截去一部分，其中EH∥A′D′，剩下的几何体是(　　)A.棱台 B．四棱柱C．五棱柱 D．六棱柱
解析：由几何体的结构特征，剩下的几何体为五棱柱，故选C.
2．圆柱的侧面展开图是边长为6π和4π的矩形，则圆柱的表面积为(　　)A．6π(4π＋3)　　　　　　　B．8π(3π＋1)C．6π(4π＋3)或8π(3π＋1) D．6π(4π＋1)或8π(3π＋2)
解析：设圆柱的底面半径为r，分两种情况．①若6π＝2πr，r＝3.∴圆柱的表面积为：4π×6π＋2πr2＝24π2＋18π＝6π(4π＋3)．②若4π＝2πr，r＝2，∴圆柱的表面积为：4π×6π＋2×πr2＝24π2＋8π＝8π(3π＋1)，故选C.
3．Rt△ABC的三个顶点都在球O的球面上，AB＝AC＝2，若球心O到平面ABC的距离为1，则球O的半径为______，球O的表面积为________．
题型一　空间几何体角度1|空间几何体的结构特征[例1]　(多选题)下列命题不正确的是(　　)A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱D．用一平面去截棱锥，截面与底面之间的部分组成的几何体叫棱台
解析：对于A，它的每相邻两个四边形的公共边不一定互相平行，故A错；对于B，也是它的每相邻两个四边形的公共边不一定互相平行，例如，两个底面全等的斜四棱柱拼接在一起，故B错；对于C，它符合棱柱的定义，故C对；对于D，它的截面与底面不一定互相平行，故D错．故选ABD.
类题通法解决与空间几何体结构特征有关问题的三个技巧 (1)把握几何体的结构特征，要多观察实物，提高空间想象能力． (2)紧扣结构特征是判断的关键，熟悉空间几何体的结构特征，依据条件构建几何模型． (3)通过反例对结构特征进行辨析．
巩固训练1：下列命题正确的是(　　)A．以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥B．以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台C．圆柱、圆锥、圆台的底面都是圆面D．一个平面截圆锥，得到一个圆锥和一个圆台
解析：由圆锥、圆台、圆柱的定义可知A，B错误，C正确．对于命题D，只有用平行于圆锥底面的平面去截圆锥，才能得到一个圆锥和一个圆台，D不正确．故选C.
角度3|展开图[例3]　纸制的正方形的六个面根据其方位分别标记为上、下、东、南、西、北．现在沿该正方体的一些棱将正方体剪开，外面朝上展平，得到如图所示的平面图形，则标“△”的面的方位是(　　)A．南 B．北 C．西 D．下
类题通法求解展开图问题的关键及注意事项 求解立体图形展开图问题的关键是弄清原有的性质变化与否．应注意： (1)点的变化，点与点的重合及点的位置变化； (2)长度、角度等几何度量的变化．
巩固训练3：如图所示是一个无盖的正方体盒子展开后的平面图，A，B，C是展开图上的三点，则在正方体盒子中，∠ABC的值为(　　)A.30° B．45°C．60° D．90°
(2)[2020·江苏卷]如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm，高为2 cm，内孔半径为0.5 cm，则此六角螺帽毛坯的体积是________cm3.
(3)(一题两空)如图，在直角梯形ABCD中，AD＝AB＝4，BC＝2，沿中位线EF折起，使得∠AEB为直角，连接AB，CD，则所得的几何体的表面积为________，体积为________．
类题通法 (1)几何体表面积的计算：根据几何体的直观图或三视图所给的条件，确定表面的形状，选择正确的平面图形的面积公式求解，注意表面积与底面积、侧面积的区别．(2)几何体体积的计算：简单几何体可用体积公式直接求解，一些组合体的体积则需用转换法、分割法、补形法等方法进行求解．
巩固训练4：(1)若圆锥的侧面展开图是圆心角为120°，半径为l的扇形，则这个圆锥的表面积与侧面积的比为(　　)A．3∶2 B．2∶1C．4∶3 D．5∶3
(3)如图，在多面体ABCDEF中，已知四边形ABCD是边长为1的正方形，且△ADE，△BCF均为正三角形，EF∥AB，EF＝2，则该多面体的体积为________．
类题通法 (1)求解多面体的外接球时，经常用到截面圆．如图所示，设球O的半径为R，截面圆O′的半径为r，M为截面圆上任意一点，球心O到截面圆O′的距离为d，则在Rt△OO′M中，OM2＝OO′2＋O′M2，即R2＝d2＋r2.(2)求解球的内接正方体、长方体等问题的关键是把握球的直径即是几何体的体对角线．(3)若球面上四点P，A，B，C的连线中PA，PB，PC两两垂直或三棱锥的三条侧棱两两垂直，则可构造长方体或正方体解决问题．
(2)(一题两空)半径为R的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为________，体积为________．
解析：S表＝πR2×2＋π×2×R×R×2＝2πR2＋4πR2＝6πR2，V＝π×R2×R×2＝2πR3.
答案：6πR2　2πR3
[预测2]　立体几何中的数学文化玉琮是中国古代玉器中重要的礼器，神人纹玉琮王是新石器时代良渚文化的典型玉器，1986年出土于浙江省余杭市反山文化遗址．玉琮王通高8.8 cm，孔径4.9 cm、外径17.6 cm.琮体四面各琢刻一完整的兽面神人图像，兽面的两侧各浅浮雕鸟纹．器形呈扁矮的方柱体，内圆外方，上下端为圆面的射，中心有一上下垂直相透的圆孔．试估计该神人纹玉琮王的体积约为(单位：cm3)(　　)A.6 250 B．3 050C．2 850 D．2 350
状 元 笔 记　球心的确定 “切”“接”问题的处理规律(1)“切”的处理解决与球有关的内切问题主要是指球内切于多面体或旋转体，解答时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作．(2)“接”的处理把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．
1．由球的定义确定球心若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球．也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体外接球的球心．①长方体或正方体的外接球的球心是其体对角线的中点；②正三棱柱的外接球的球心是上、下底面中心连线的中点；③直三棱柱的外接球的球心是上、下底面三角形外心连线的中点；④正棱锥的外接球的球心在其高上，具体位置可通过建立直角三角形运用勾股定理计算得到．
[典例1]　若正三棱柱ABC－A ′B ′C ′的底面边长为2，侧棱长为1，其顶点都在同一球面上，则球的表面积为________．
2．构造长方体或正方体确定球心①正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补成长方体或正方体；②同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥，可将三棱锥补成长方体或正方体；③若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体；④若三棱锥的三个侧面两两垂直，则可将三棱锥补成长方体或正方体．
【探究】　本题运用公式R2＝r2＋d2(r为三棱锥底面外接圆的半径，R为三棱锥外接球的半径，d为球心到三棱锥底面中心的距离)求球的半径，该公式是求球的半径的常用式．本题的思路是探求正棱锥外接球半径的通法，该方法的实质是通过寻找外接球的一个轴截面，把立体几何问题转化为平面几何问题来研究．