高中人教A版 (2019)1.5 全称量词与存在量词评优课课件ppt

这是一份高中人教A版 (2019)1.5 全称量词与存在量词评优课课件ppt，共30页。PPT课件主要包含了word部分，点击进入链接等内容，欢迎下载使用。
全称量词命题和存在量词命题的否定
你知道的常见量词有哪些？它们的否定是什么？提示：常见量词及其否定：
1．判断正误(正确的打“√”，错误的打“×”)(1)命题“∀x∈{x|x≥0}，x3＋x≥0”的否定是“∀x∈{x|x≥0}，x3＋x＜0”．(　　)(2)∃x∈M，p(x)与∀x∈M，¬p(x)的真假性相反．(　　)(3)从存在量词命题的否定看，是对“量词”和“p(x)”同时否定．(　　)
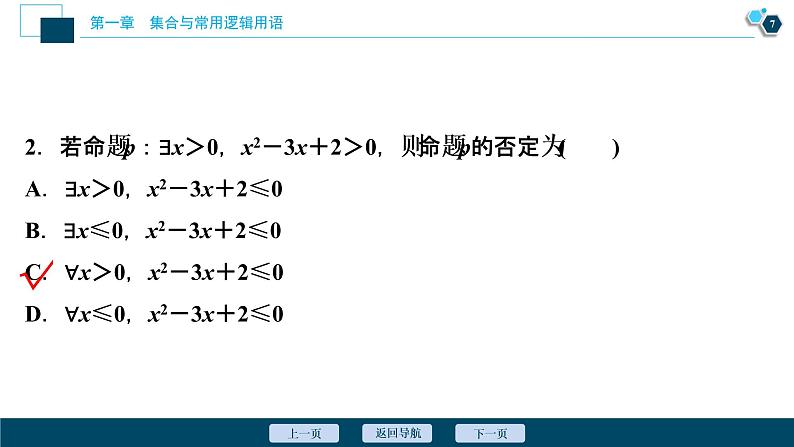
2．若命题p：∃x＞0，x2－3x＋2＞0，则命题p的否定为(　　)A．∃x＞0，x2－3x＋2≤0B．∃x≤0，x2－3x＋2≤0C．∀x＞0，x2－3x＋2≤0D．∀x≤0，x2－3x＋2≤0
3．已知命题p：∀x＞2，x3－8＞0，那么p的否定是________．答案：∃x＞2，x3－8≤0
探究点1　全称量词命题的否定[问题探究]如何写全称量词命题的否定？提示：写全称量词命题的否定的方法：(1)更换量词，将全称量词换为存在量词．(2)将结论否定．
写出下列全称量词命题的否定：(1)任何一个平行四边形的对边都平行；(2)∀a∈R，方程x2＋ax＋2＝0有实数根；(3)∀a，b∈R，方程ax＝b都有唯一解；(4)可以被5整除的整数，末位是0.【解】　(1)该命题的否定是存在一个平行四边形，它的对边不都平行．(2)该命题的否定是∃a∈R，方程x2＋ax＋2＝0没有实数根．(3)该命题的否定是∃a，b∈R，使方程ax＝b的解不唯一或不存在．(4)该命题的否定是存在被5整除的整数，末位不是0.
写全称量词命题的否定的两个关注点(1)写出全称量词命题的否定的关键是找出全称量词命题的全称量词和结论，把全称量词改为存在量词，结论变为否定的形式就得到命题的否定.(2)有些全称量词命题省略了量词，在这种情况下，千万不要将否定写成“是”或“不是”．　
写出下列全称量词命题的否定：(1)所有自然数的平方都是正数；(2)任何实数x都是方程5x－12＝0的根；(3)对任意实数x，x2＋1≥0.解：(1)该命题的否定是有些自然数的平方不是正数．(2)该命题的否定是存在实数x不是方程5x－12＝0的根．(3)该命题的否定是存在实数x，使得x2＋1＜0.
探究点2　存在量词命题的否定[问题探究]如何写存在量词命题的否定？提示：写存在量词命题的否定的方法：(1)将存在量词改写为全称量词．(2)将结论否定．
写存在量词命题的否定的关注点注意对不同的存在量词的否定的写法，例如，“存在”的否定是“任意的”，“有一个”的否定是“所有的”或“任意一个”等．　
探究点3　求参数的取值范围 已知命题p：∀x∈R，ax2＋2x＋1≠0，q：∃x∈R，ax2＋ax＋1≤0.若p与q均为假命题，求实数a的取值范围．【解】　因为p：∀x∈R，ax2＋2x＋1≠0，q：∃x∈R，ax2＋ax＋1≤0，所以¬p：∃x∈R，ax2＋2x＋1＝0，¬q：∀x∈R，ax2＋ax＋1＞0.由题意得¬p与¬q都是真命题．
利用含量词的命题的真假求参数的取值范围(1)含参数的全称量词命题为真时，常与不等式恒成立有关，可根据有关代数恒等式(如x2≥0)，确定参数的取值范围．(2)含参数的存在量词命题为真时，常转化为方程或不等式有解问题来处理，可借助根的判别式等知识解决．　
1．命题“∃x∈R，x2－2x－3≤0”的否定是(　　)A．∀x∈R，x2－2x－3≤0B．∃x∈R，x2－2x－3≥0C．∃x∈R，x2－2x－3＞0D．∀x∈R，x2－2x－3＞0解析：存在量词命题的否定是全称量词命题，一方面要改量词即“∃”改为“∀”；另一方面要否定结论，即“≤”改为“＞”．故选D．
2．对下列命题的否定，其中说法错误的是(　　)A．p：∀x≥3，x2－2x－2≥0；p的否定：∃x≥3，x2－2x－2＜0B．p：存在一个四边形的四个顶点不共圆；p的否定：每一个四边形的四个顶点共圆C．p：有的三角形为正三角形；p的否定：所有的三角形不都是正三角形D．p：∃x∈R，x2＋2x＋2≤0；p的否定：∀x∈R，x2＋2x＋2＞0解析：若p：有的三角形为正三角形，则p的否定：所有的三角形都不是正三角形，故C错误．
4．写出下列命题的否定，并判断其否定的真假．(1)菱形是平行四边形；(2)∀x≥0，x2＞0；(3)存在一个三角形，它的内角和大于180°；(4)∃x∈R，x2＋x＋1≤0.
请做：应用案　巩固提升