初中数学人教版八年级上册第十二章 全等三角形综合与测试练习题

这是一份初中数学人教版八年级上册第十二章 全等三角形综合与测试练习题，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共7小题；共35分）
1. 如图是用直尺和圆规作角平分线的示意图，通过证明 △DOP≌△EOP 可以说明 OC 是 ∠AOB 的角平分线，那么 △DOP≌△EOP 的依据是
A. SSSB. SASC. ASAD. AAS

2. 如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，最省事的方法是
A. 带①去B. 带②去C. 带③去D. 带①和②去

3. 如图，已知 DE⊥BC，BE=EC，且 AB=7，AC=8，则 △ABD 的周长为
A. 15B. 20C. 25D. 30

4. 如图所示，两条笔直的公路 l1，l2 相交于点 O，C 村的村民在公路的旁边建三个加工厂 A，B，D，已知 C 村在 ∠BAD 的角平分线上，C 村到公路 l1 的距离 4 km，则 C 村到公路 l2 的距离是
A. 3 kmB. 4 kmC. 5 kmD. 6 km

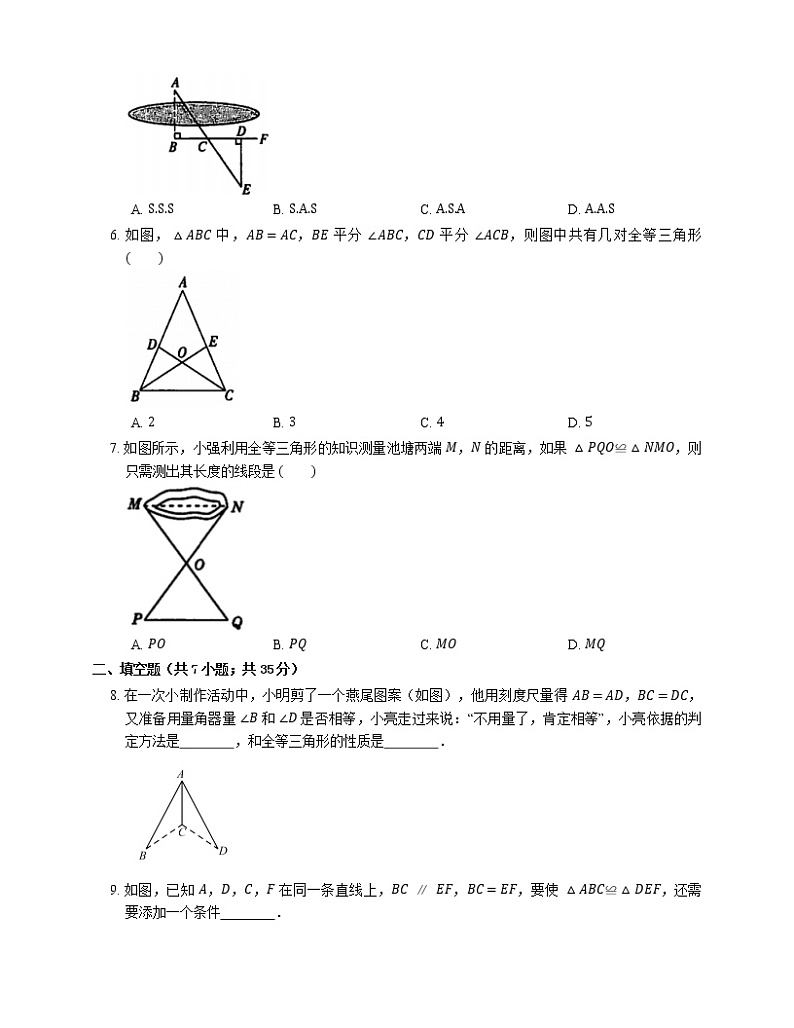
5. 如图，要量湖两岸相对两点 A，B 的距离，可以在 AB 的垂线 BF 上取两点 C，D，使 CD=BC，再作出 BF 的垂线 DE，使 A，C，E 在一条直线上，这时可得 △ABC≌△EDC，用于判定全等的根据是
A. S.S.SB. S.A.SC. A.S.AD. A.A.S

6. 如图，△ABC 中，AB=AC，BE 平分 ∠ABC，CD 平分 ∠ACB，则图中共有几对全等三角形
A. 2B. 3C. 4D. 5

7. 如图所示，小强利用全等三角形的知识测量池塘两端 M，N 的距离，如果 △PQO≌△NMO，则只需测出其长度的线段是
A. POB. PQC. MOD. MQ
二、填空题（共7小题；共35分）
8. 在一次小制作活动中，小明剪了一个燕尾图案（如图），他用刻度尺量得 AB=AD，BC=DC，又准备用量角器量 ∠B 和 ∠D 是否相等，小亮走过来说：“不用量了，肯定相等”，小亮依据的判定方法是 ，和全等三角形的性质是 ．

9. 如图，已知 A，D，C，F 在同一条直线上，BC∥EF，BC=EF，要使 △ABC≌△DEF，还需要添加一个条件 ．

10. 如图，△ABC 的三个顶点分别在格子的 3 个顶点上，请你试着在格子的顶点上找出一个点 D，使得 △DBC 与 △ABC 全等．
（1）这样的点 D 共有 个；
（2）把这样的三角形都画出来．

11. 如图，D，E 是 △ABC 的边 AC，BC 上的点，△ADB≌△EDB≌△EDC，下列结论：① AD=ED；② BC=2AB；③ ∠1=∠2=∠3；④ ∠4=∠5=∠6；⑤ ∠A=90∘；⑥ DE⊥BC．其中正确的是 （写编号）．

12. 通过 的两个三角形叫全等三角形．

13. 平行四边形中的一条对角线把平行四边形分成 个全等三角形，两条对角线把平行四边形分成 对全等三角形．

14. 如图，OP 平分 ∠MON，PE⊥OM 于 E，PF⊥ON 于 F，OA=OB，则图中有 对全等三角形．
三、解答题（共6小题；15,16题各14分，17-20题各13分，共80分）
15. 尺规作图（保留作图痕迹，写出作法）．
如图，已知 ∠α．
求作：
（1）∠AOB，使 ∠AOB=∠α；
（2）射线 OP，使 OP 平分 ∠AOB．

16. 已知 △ABC．
（1）请用直尺和圆规作一个三角形，使所画三角形与 △ABC 全等；
（2）请简要说明你所作的三角形与 △ABC 全等的依据．

17. 如图，太阳光线 AC 与 AʹCʹ 是平行的，同一时刻两根高度一样的垂直木杆在阳光的照射下的影子也是一样长的，请说明这是为什么?

18. 如图，在四边形 ABCD 中，AB=AF，AE 是 ∠BAF 的平分线．
（1）求证 △ABE≌△AFE；
（2）若 AB∥DC，求证：∠AFD=∠C．

19. 如图，OP 平分 ∠AOB，∠AOB=40∘，PM⊥OA 于点 M，PN⊥OB 于点 N，PC∥OB，交边 OA 于点 C，E 为边 OB 上的一点，且满足 PC=PE，求 ∠EPN 的度数．

20. 画图探究并验证你的猜想：
在四边形 ABCD 中，已知 AB+CD=BC，AB⊥BC，CD⊥BC．是否能在 BC 上作一点 E，使 △ABE≌△ECD，如果能找到 E 点，画图并证明你的猜想，并说明 E 点的位置．
答案
1. A
2. C
3. A
4. B
5. C
6. B【解析】∵AB=AC，
∴∠ACB=∠ABC，
∵BE 平分 ∠ABC，CD 平分 ∠ACB，
∴∠ACD=∠ABE，
在 △ACD 和 △ABE 中，∠A=∠A,AC=AB,∠ACD=∠ABE,
∴△ACD≌△ABEASA，
∴AD=AE，DC=EB，
∴AB-AD=AC-AE，即 BD=CE，
在 △DCB 和 △EBC 中，BD=CE,BC=CB,DC=EB,
∴△DCB≌△EBCSSS．
在 △BOD 和 △COE 中，∠DOB=∠EOC,∠DBO=∠ECO,BD=CE,
∴△BOD≌△COEAAS．
∴ 共有 3 对全等三角形，△ACD≌△ABE，△DCB≌△EBC，△BOD≌△COE．
7. B【解析】由全等三角形对应边相等的性质可知，只需测出 MN 的对应边的长，
因为 △PQO≌△NMO，
所以 PQ=MN，
所以只需测出 PQ 的长度即可．
8. SSS，全等三角形对应角相等
9. 答案不唯一，如 ∠B=∠E，AC=DF 等
10. 3，如图所示
11. ①②③④⑤⑥
12. 图形运动后能完全重合
13. 2，4
14. 3
【解析】因为 OP 平分 ∠MON，
所以 ∠AOP=∠BOP，
因为 OA=OB，OP=OP，
所以 △OAP≌△OBPSAS．
所以 AP=BP．
因为 PE⊥OM，PF⊥ON，
所以 ∠OEP=∠OFP=90∘，
又因为 ∠AOP=∠BOP，OP=OP，
所以 △OEP≌△OFPAAS．
所以 PE=PF．
所以 Rt△AEP≌Rt△BFPHL．
15. （1）
作法：
①作射线 OA ；
②以 Q 为圆心，画弧交 ∠Q 两边于 M，N；
③以 O 为圆心，QM 长为半径画弧交 OA 于 C ；
④以 C 为圆心，MN 长为半径画弧，两弧交于点 B ；
⑤作射线 OB，∠AOB 即为所求．
（2）
作法：①分别以 B，C 为圆心，大于 12BC 长为半径画弧，两弧交于点 P ；
②作射线 OP，OP 即为所求．
16. （1） 如图所示：△EDF 即为所求；
（2） 在 △EDF 和 △ABC 中，
DE=AB,DF=BC,EF=AC,
∴ △EDF≌△ABCSSS．
17. 因为 AC∥AʹCʹ，
所以 ∠ACB=∠AʹCʹBʹ．
又因为 ∠ABC=∠AʹBʹCʹ=90∘，AB=AʹBʹ，
所以 △ABC≌△AʹBʹCʹ，
所以 BC=BʹCʹ．
18. （1） 因为 AE 是 ∠BAF 的平分线，
所以 ∠BAE=∠FAE．
又因为 AB=AF，AE=AE，
所以 △ABE≌△AFE（SAS）．
（2） 因为 △ABE≌△AFE，
所以 ∠B=∠AFE．
因为 AB∥CD，
所以 ∠B+∠C=180∘．
又因为 ∠AFE+∠AFD=180∘，
所以 ∠AFD=∠C．
19. ∵ OP 平分 ∠AOB，PM⊥OA，PN⊥OB，
∴ PM=PN，
在 Rt△PMC 和 Rt△PNE 中，
PC=PE,PM=PN,
∴ Rt△PMC≌Rt△PNEHL，
∴ ∠EPN=∠CPM，
∵ PC∥OB，
∴ ∠PCM=∠AOB=40∘，
∵ PM⊥AO，
∴ ∠CPM=90∘-40∘=50∘，
∴ ∠EPN=50∘．
20. 在 BC 上截取 BE=CD，
∵ AB+CD=BC，
∴ AB=EC，
∵ AB⊥BC，CD⊥BC，
∴ ∠B=∠C=90∘，
在 △ABE 和 △ECD 中，AB=EC,∠B=∠C=90∘,EB=CD,
∴ △ABE≌△ECDSAS，
E 的位置有三种可能的情况：（1）若 ABDC，点 E 在 BC 上靠近点 B 处．