高中北师大版3二倍角的三角函数教案

§3二倍角的三角函数

【教学目标】

1.知识与技能:能从两角和的正弦、余弦、正切公式导出二倍角的正弦、余弦、正切公式，了解它们的内在联系；

2.过程与方法: 通过公式的推导，了解 公式之间的 内在联系从 而培养逻辑推理能力；综合运用公式，掌握有关的技巧，提高分析问题，解决问题的能力；

3.情感态度与价值观: 通过公式推导，了解和角与倍角公式之间的内在联系，领会从一般到特殊的数学思想，强化学生的参与意识，并培养学生综合分析能力.

【教学重点】

二倍角公式，变形式及其应用．

【教学难点】

倍角公式与同角三角函数基本关系式，诱导公式，和角公式的综合应用．

【教学方法】

本节课采用观察、赋值、启发探究相结合的教学方法，运用现代多媒体教学手段，进行教学活动，在思考、探索和交流的过程中获得倍角公式；对于二倍角公式的灵活运用，采用讲、练结合的方式进行处理。

【教学过程】

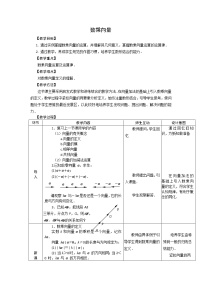
1.二倍角公式的推导

首先，请大家回顾我们前面学习的两角和的正弦、余弦、正切公式：

在这里，如果我们令即可得到以下公式：

简记：

   简记：

简记：

在中右端既有又有，利用公式可得得另两种表示形式：.

这就是我们这节课要来认识的二倍角公式.

需要注意的是：对“二倍角”的认识，如是的二倍，是的二倍，是 的二倍，是的二倍，二倍角是相对的；余弦二倍角公式有三种形式，要恰当地选择以便简化运算过程．对二倍角公式要学会灵活应用（顺用、逆用、变用）．

2. 二倍角公式的变形

容易得到以下公式：（降幂公式）

3.公式的初步运用

[例1]已知，求，，的值。

解：∵，  ∴．

∴；

；．

[练习1]　求证：．

分析：消除角的差异,把不同的角化为相同的角，在化简的过程中注意选取合适的公式．

[练习2]利用倍角公式求下列各式的值．

①②
③ 1－④

4.公式的综合运用

[例2]已知tanα，tanβ是方程x2＋3x＋4＝0的两个实根，且α，β∈(，)，求α＋β的值．

解：由于tanα，tanβ是方程x2＋3 x＋4＝0的两个实根，

于是

∵α，β∈(，)，由②知tanα与tanβ同号，结合①知tanα<0，tanβ<0，

∴<α<π，<β<π，

∴π<α＋β<2π

而tan(α＋β)＝＝＝，∴α＋β＝.

[练习3]三角形ABC中，，求的值

[例3]已知函数f(x)＝2sinxcosx＋2cos2x.

(1)求函数f(x)的单调递增区间；

(2)将函数y＝f(x)的图像向右平移个单位后，得到函数y＝g(x)的图像，求方程g(x)＝1在x∈[0，π]上的解集．

解：(1)f(x)＝sin(2x＋)＋1，由2kπ－≤2x＋≤2kπ＋(k∈Z)得：

kπ－≤x≤kπ＋，

∴f(x)的单调递增区间是[kπ－，kπ＋](k∈Z)．

(2)由已知，g(x)＝sin(2x－)＋1，由g(x)＝1，得sin(2x－)＝0，

∴x＝＋(k∈Z)，∵x∈[0，π]，∴x＝或，

∴方程的解集为{，}．

【课堂小结】

1．本节课主要学习了二倍角的几组公式：

（1）

（2）=1－=．

（3）．

2. 我们一起推导了二倍角的公式，明白了从一般到特殊的思想，并运用二倍角公式解题．在解题的时候要注意分析三角函数名称、角的关系，选择最佳解决问题的途径，以达到优化解题过程的目的．

3.在解决三角函数式的化简问题时，经常从以下三个方面来考虑：一看函数式中所涉及的角之间的关系；二看函数式中所涉及的三角函数的名称之间的关系；三看所涉及的函数的幂．遵循的原则是：不同角化同角，不同名化同名，高次降低次．

【板书设计】

       §3二倍角的三角函数

1. 倍角公式        2.公式的运用

1 例1           3  例3

                2例2

【教学反思】

1. 在采用观察、赋值、启发探究相结合的方法推导公式的过程中，多引导学生复习公式，发现问题，提出解决问题的方法，增强学生的参与度。

2.在题目的解决中，例题1、例题2可以先让学生尝试，为提高效率、不耽搁进度，可以将2个问题交给两组不同的同学。