高三理科数学一轮单元卷：第十四单元 空间几何体 B卷

这是一份高三理科数学一轮单元卷：第十四单元 空间几何体 B卷，共13页。试卷主要包含了选择题的作答，非选择题的作答等内容，欢迎下载使用。
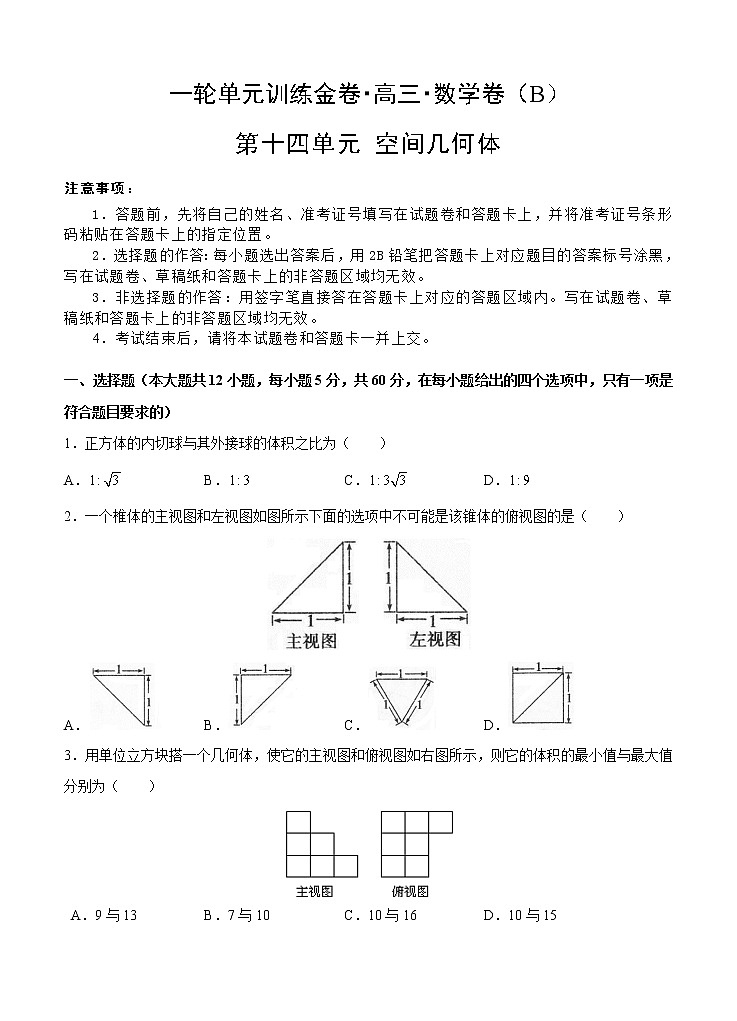
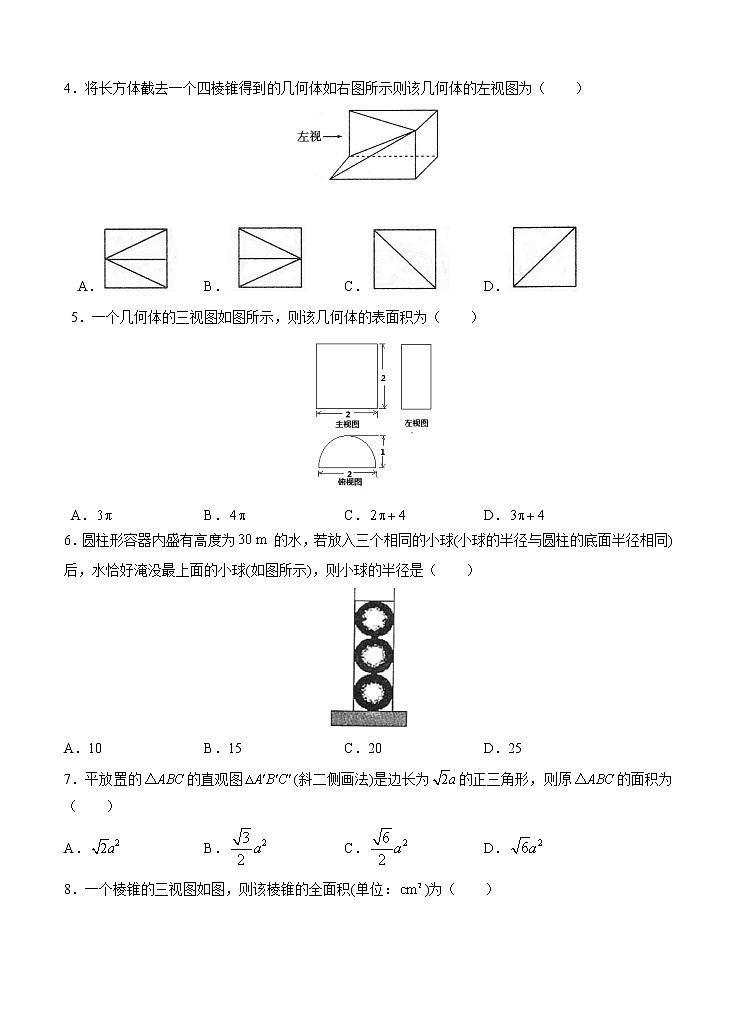
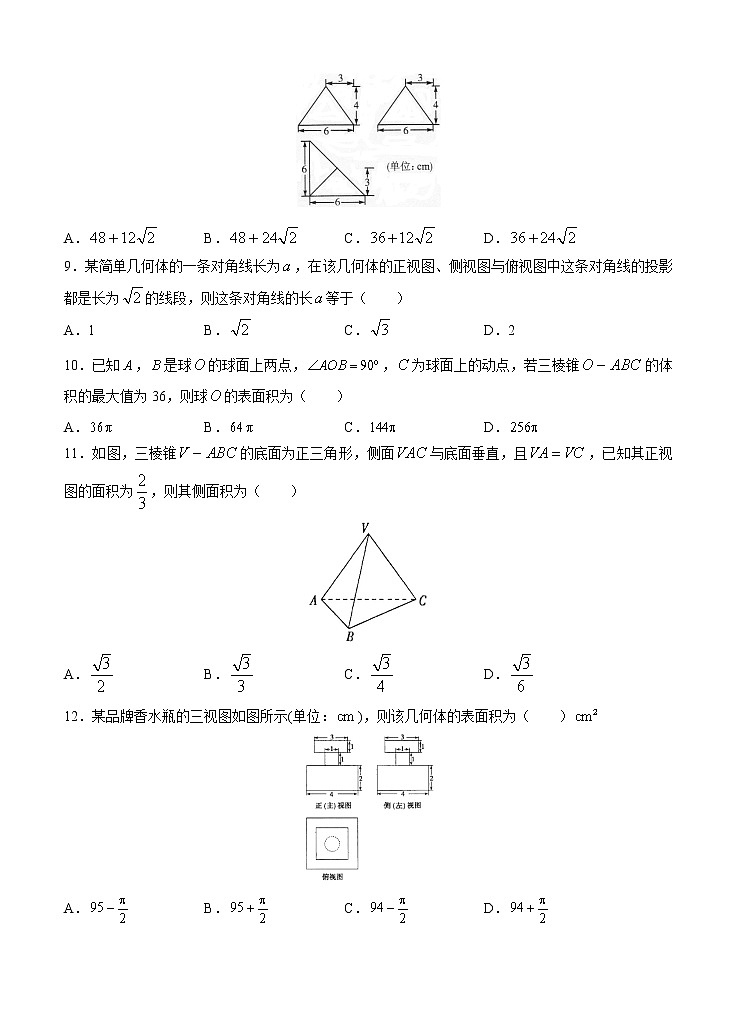
一轮单元训练金卷▪高三▪数学卷（B）第十四单元 空间几何体注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。4．考试结束后，请将本试题卷和答题卡一并上交。一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．正方体的内切球与其外接球的体积之比为（    ）A． B． C． D．2．一个椎体的主视图和左视图如图所示下面的选项中不可能是该锥体的俯视图的是（    ）A． B． C． D．3．用单位立方块搭一个几何体，使它的主视图和俯视图如右图所示，则它的体积的最小值与最大值分别为（    ）A．9与13 B．7与10 C．10与16 D．10与154．将长方体截去一个四棱锥得到的几何体如右图所示则该几何体的左视图为（    ） A． B． C． D．5．一个几何体的三视图如图所示，则该几何体的表面积为（    ）A． B． C． D．6．圆柱形容器内盛有高度为的水，若放入三个相同的小球(小球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的小球(如图所示)，则小球的半径是（    ）A．10 B．15 C．20 D．257．平放置的的直观图(斜二侧画法)是边长为的正三角形，则原的面积为（    ）A． B． C． D． 8．一个棱锥的三视图如图，则该棱锥的全面积(单位：)为（    ）A． B． C． D．9．某简单几何体的一条对角线长为，在该几何体的正视图、侧视图与俯视图中这条对角线的投影都是长为的线段，则这条对角线的长等于（    ）A．1 B． C． D．210．已知，是球的球面上两点，，为球面上的动点，若三棱锥的体积的最大值为36，则球的表面积为（    ）A． B． C． D．11．如图，三棱锥的底面为正三角形，侧面与底面垂直，且，已知其正视图的面积为，则其侧面积为（    ）A． B． C． D．12．某品牌香水瓶的三视图如图所示(单位：)，则该几何体的表面积为（    ）A． B． C． D． 二、填空题（本大题有4小题，每小题5分，共20分．请把答案填在题中横线上）13．一块边长为的正方形铁片按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角形作侧面，以它们的公共顶点为顶点，加工成一个如图所示的正四棱锥容器，当时，该容器的容积为________．14．有一个几何体的三视图及其尺寸如图所示，则该几何体的表面积为______．15．一个几何体的三视图如图所示，则该几何体的表面积为______．16．某几何体的三视图如图，则该几何体的体积的最大值为______． 三、解答题（本大题有6小题，共70分．解答应写出文字说明、证明过程或演算步骤）17．（10分）已知四棱锥的体积为，其三视图如图所示，其中正视图为等腰三角形，侧视图为直角三角形，俯视图是直角梯形．（1）求正视图的面积；（2）求四棱锥的侧面积．18．（12分）一个倒立的圆锥形容器，它的轴截面是正三角形，在这容器内注入水并且放入一个半径为的铁球，这时水面恰好和球面相切，求将球从圆锥内取出后，圆锥内水平面的高(结果用表示)． 19．（12分）如图所示，正的边长为，是边上的高，，分别是，的中点，现将沿翻折，使翻折后平面平面．（1）试判断翻折后直线与平面的位置关系，并说明理由；（2）求三棱锥的体积． 20．（12分）已知四面体的六条棱中，有五条棱长都等于．（1）求该四面体体积的最大值；（2）当四面体的体积最大时，求其表面积．   21．（12分）如图，四边形为正方形，平面，，．（1）证明：平面；（2）求棱锥的体积与棱锥的体积的比值．   22．（12分）已知三棱柱的三视图如下图所示，其中正视图和侧视图均为矩形，俯视图中，，，．（1）在三棱柱中，求证：；（2）在三棱柱中，若是底边的中点，求证：平面；（3）若三棱柱的高为5，求三视图中侧视图的面积．    一轮单元训练金卷▪高三▪数学卷答案（B）第十四单元 空间几何体一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．【答案】C【解析】设正方体的棱长为，则它的内切球的半径为，它的外接球的半径为，故所求的比为，故选C．2．【答案】C【解析】由于C选项中的俯视图与左视图中的宽不等，故选C．3．【答案】C【解析】由于主视图中每列的层数就是俯视图中该列的最大数字，因此，用方块最多的情况是每列都用最大数字，即，最少的情况是每列只有一个用最大数字，其余的各列为1个方块，即，故选C．4．【答案】D【解析】如图，在侧面上的射影与重合，在侧面上的射影与重合，在侧面上的射影与重合，故选D．5．【答案】D【解析】根据几何体的三视图可知，该几何体半个圆柱体(沿中心轴线分开)，圆柱的高为2，底面圆的半径为1，该几何体的表面积为：．故选D．6．【答案】B【解析】设小球的半径为，根据放入小球的先后水的体积相同，得，解得．故选B．7．【答案】D【解析】由斜二侧画法中知：原图面积与直观图面积之比为．设原的面积为，则易知，∴．故选D．8．【答案】A【解析】由三视图可知，原棱锥为三棱锥，底面是直角边长为6的等腰直角三角形，高为4，把该三棱锥记为，易知顶点在底面的射影为底面等腰直角三角形斜边的中点，且，．则全面积为：，故选A．9．【答案】C【解析】可以把该几何体想象为一长方体，设，则由题意知，设长方体的长、宽、高分别为、、，则，，三式相加得．∴．故选C．10．【答案】C【解析】设球的半径为，当动点与平面垂直时，三棱锥的体积达到最大值，且，∴，∴球的表面积为，故选C．11．【答案】B【解析】由题意知该三棱锥的正视图为，作于，连接，设底面边长为，高为，则的面积为，又三棱锥的正视图为的面积为，故选B．12．【答案】D【解析】由三视图可知该几何体上下为长方体，中间为圆柱，，故选D． 二、填空题（本大题有4小题，每小题5分，共20分．请把答案填在题中横线上）13．【答案】【解析】正四棱锥的高，()．14．【答案】【解析】由三视图可知，这是一个三棱锥，，，∴，∴．15．【答案】【解析】由三视图可知，该几何体由一个正方体和一个四棱柱组成，其表面积为．16．【答案】【解析】由三视图知该几何体为三棱锥记为，其中面，底面为直角三角形．，设，，，则．利用不等式得，∴．又体积． 三、解答题（本大题有6小题，共70分．解答应写出文字说明、证明过程或演算步骤）17．【答案】（1）；（2）．【解析】（1）如图所示四棱锥的高为，底面积为，∴四棱锥的体积，∴，∴正视图的面积为．（2）如图所示，过作交于，连接．根据三视图可知，是的中点，且，，且，，又平面，∴，，，∴面，∴，又，∴面，∴，且平面．∴，∴．∴．∴四棱锥的侧面积为．18．【答案】【解析】设球未取出时高为，球取出后水面高度，如图所示，∵，，∴以为底面直径的圆锥容器的容积为，，球取出水面下降到，水的体积为：，而，即，∴，即球取出后水面的高度为．19．【答案】（1）平面，见解析；（2）．【解析】（1）判断平面，证明如下：因为中，，分别是，的中点，所以有，又因为平面，平面，所以平面．（2）过点作于点，平面平面，平面平面，而平面，故平面，所以是三棱锥的高．又的面积为：．，故三棱锥的体积为：．20．【答案】（1）；（2）．【解析】（1）如图，在四面体中，设，，取的中点，的中点为，连接、、，得到平面，∴．当且仅当时取到等号，所以该四面体体积的最大值为．（2）由（1）知，和都是边长为的正三角形，和是全等的等腰三角形，其腰长为，底边长为，∴．21．【答案】（1）见解析；（2）．【解析】（1）由条件知四边形为直角梯形，因为平面，所以平面平面，交线为．又因为四边形为正方形，，所以平面，可得．在直角梯形中可得，则．又，所以平面．（2）设，由题意知为棱锥的高，所以的体积．由（1）知为棱锥的高，而，的面积为，所以棱锥的体积为．故棱锥的体积与棱锥的体积的比值为．22．【答案】（1）见解析；（2）见解析；（3）12．【解析】（1）证明：因为主视图和左视图均为矩形，所以该三棱柱为直三棱柱，在俯视图中，，，．由余弦定理得：， ∴，∴．又∵，，∴平面．∵平面，∴．（2）连结交于点，则为的中点，连结， 则在中，．∵平面，平面，∴平面．（3）左视图中的长等于底面中顶点到边的距离，∵，∴侧视图的面积．