人教A版 (2019)必修 第一册4.1 指数课前预习ppt课件

这是一份人教A版 (2019)必修 第一册4.1 指数课前预习ppt课件，共34页。PPT课件主要包含了教学目标，学科素养，知识回顾，整数指数幂，新知探索，正数的正分数指数幂，正数的负分数指数幂，拓展提升，归纳总结，课后作业等内容，欢迎下载使用。

n次方根与分数指数幂
Retrspective Knwledge
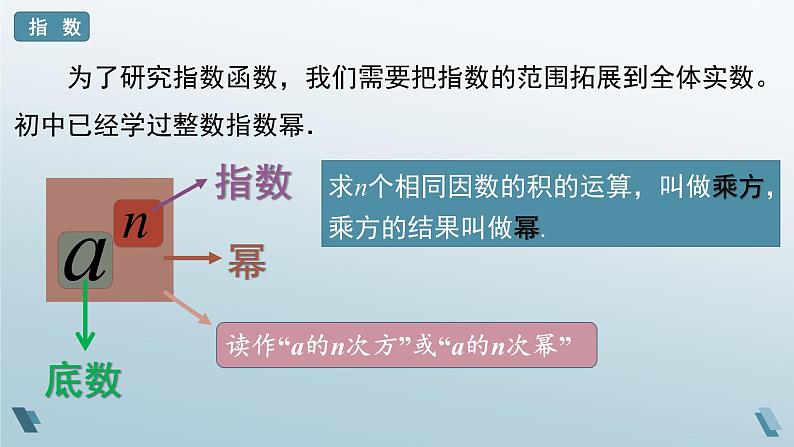
为了研究指数函数，我们需要把指数的范围拓展到全体实数。初中已经学过整数指数幂．
读作“a的n次方”或“a的n次幂”
求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂.
整数指数幂的运算性质：
New Knwledge explre
因为(±4)2 =16，所以±4叫做16的平方根;
因为(±3)2 =9，所以±3叫做9的平方根；
因为23=8，所以2叫做8的立方根；
因为(-2)3=-8，所以-2叫做-8的立方根；
如果x2=a，那么x叫做a的平方根；
如果x3=a，那么x叫做a的立方根；
类似地， 因为(±2)4=16，我们把±2叫做16的4次方根; 因为25=32，我们把2叫做32的5次方根；
n次方根定义: 一般地，如果xn=a，则x叫做a的n次方根，其中n>1，且n∈N*．
负数有没有偶次方根，因为任何实数的偶次方都是非负数.
n次方根定义: 一般地，如果xn=a，则x叫做a的n次方根，其中n>1，且n∈N*．
例1 求下列各式的值：
把根式表示为分数指数幂的形式的时候，例如：
规定： 0的正分数指数幂等于0，0的负分数指数幂没意义．
一般的，无理数指数幂 aα（a>0，α为无理数）是一个确定的实数，幂中的指数的取值范围就从整数拓展到了有理数，并拓展到了实数． 实数指数幂是一个确定的实数．对任意实数r，s，均有下面的性质：
例2 求下列各式的值：
根式化简与求值的思路及注意点：(1)思路：首先要分清根式为奇次根式还是偶次根式，然后运用根式的性质 进行化简．(2)注意点： ①正确区分“ ”与“ ”两式；（注意分析 是否有意义） ②运算时注意变式、整体代换，以及平方差、立方差和完全平方公式、完全立方公式的运用，必要时要进行讨论．
例3 用分数指数幂的形式表示下列各式：
例4 计算下列各式（式子中的字母均是正数）：
Expansin And Prmtin
利用指数幂的运算性质化简求值的方法：（1）进行指数幂的运算时，一般化负指数为正指数，化根式为分数指数 幂，化小数为分数，同时兼顾运算的顺序；（2）在明确根指数的奇偶(或具体次数)时，若能明确被开方数的符号， 则可以对根式进行化简运算；（3）对于含有字母的化简求值的结果，一般用分数指数幂的形式表示．
规定：0的正分数指数幂等于0，0的负分数指数幂没意义．
Hmewrk After Class