中考提升四边形十字架模型（一）专题练习试卷

中考提升--十字架模型（一）

1．如图，点O是正方形ABCD的中心，E、F、G、H分别是边AB、CD、BC、AD上的点，且EF⊥GH，EF、GH相交于点O，下列结论：①AE＝BG；②∠BEO＝∠CGO；③OE＝OH；④S正方形ABCD≠4S四边形AEOH中正确的有（　　）

A．1个 B．2个 C．3个 D．4个

2．如图，在边长为4的正方形ABCD中，点E、F分别是边BC、CD上的动点．且BE＝CF，连接BF、DE，则BF+DE的最小值为（　　）

A． B． C． D．

3．如图所示，正方形ABCD中，E为BC边上一点，连接AE，作AE的垂直平分线交AB于G，交CD于F，若BG＝2BE，则DF：CF的长为（　　）

A． B． C． D．

4．已知正方形ABCD的边长为4，点P是边CD上一点，且CP＝3，连接BP，Q为BP的中点，过点Q作QM⊥PB交AC于点M，连接MB，MP，则MQ的长为（　　）

A．4 B．5 C． D．3

5．如图，已知正方形ABCD的边长为12，BM＝CN＝5，CM、DN交于点O．则下列结论：①DN⊥MC；②DN垂直平分MC；③S△ODC＝S四边形BMON；④OC＝中，正确的有（　　）

A．1个 B．2个 C．3个 D．4个

6．如图，在正方形ABCD中，点E，F分别在BC，CD上，AE＝AF，AC与EF相交于点G．下列结论：①AC垂直平分EF；②BE+DF＝EF；③当∠DAF＝15°时，△AEF为等边三角形；④当∠EAF＝60°时，∠AEB＝∠AEF．其中正确的结论是（　　）

A．①③ B．②④ C．①③④ D．②③④

7．如图，在正方形ABCD中，点E、F分别在BC，CD上，△AEF是等边三角形，连接AC交EF于点G，下列结论：①BE＝DF；②∠DAF＝15°；③AC垂直平分EF；④BE+DF＝EF；⑤S△CEF＝2S△ABE．其中正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个

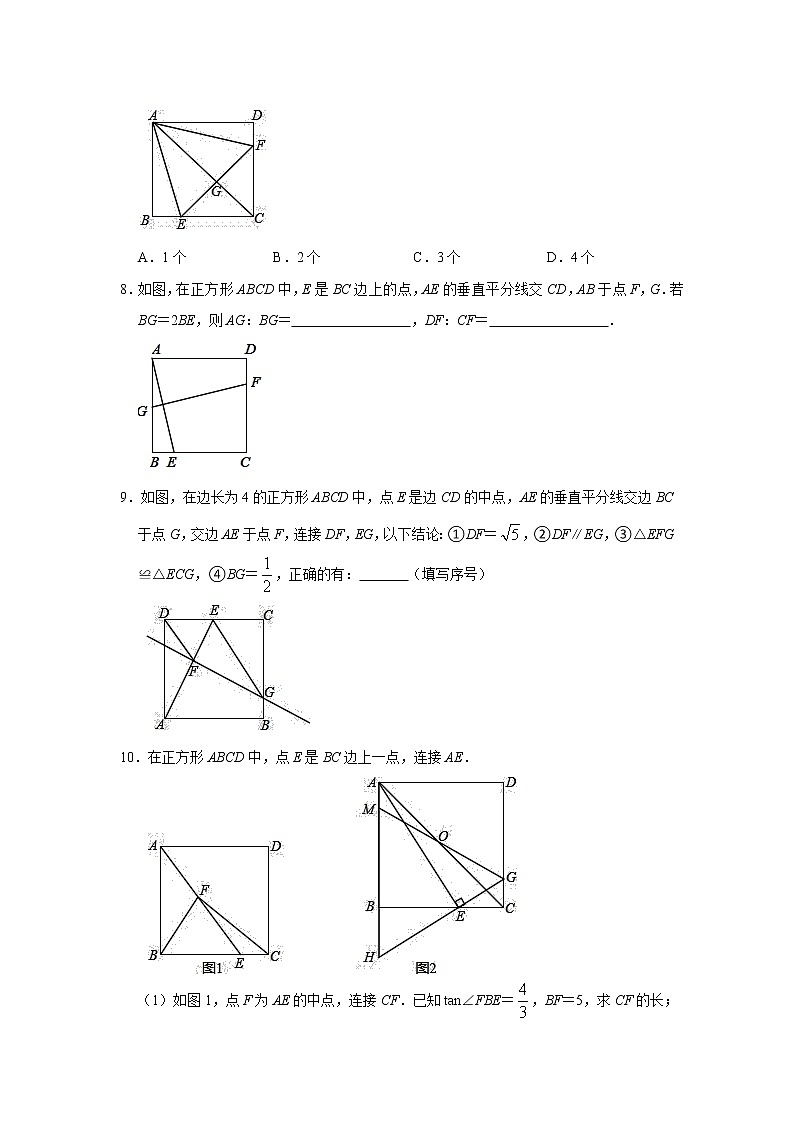
8．如图，在正方形ABCD中，E是BC边上的点，AE的垂直平分线交CD，AB于点F，G．若BG＝2BE，则AG：BG＝　             　，DF：CF＝　             　．

9．如图，在边长为4的正方形ABCD中，点E是边CD的中点，AE的垂直平分线交边BC于点G，交边AE于点F，连接DF，EG，以下结论：①DF＝，②DF∥EG，③△EFG≌△ECG，④BG＝，正确的有：　   　（填写序号）

10．在正方形ABCD中，点E是BC边上一点，连接AE．

（1）如图1，点F为AE的中点，连接CF．已知tan∠FBE＝，BF＝5，求CF的长；

（2）如图2，过点E作AE的垂线交CD于点G，交AB的延长线于点H，点O为对角线AC的中点，连接GO并延长交AB于点M，求证：AM+BH＝BE．

11．如图，在正方形ABCD中，E是CD边上一点（与C、D不重合），DF⊥AE，垂足为G，交BC于F．

（1）求证：AE＝DF；

（2）连接AF，若E是CD的中点，且CD＝4，求△AFG的面积．

（3）连接BG，若E是CD的中点．且BG＝4，求正方形ABCD的面积．

12．已知在正方形ABCD中，E为BC边上一点，F为CD边上一点．

（1）若AE＝BF．

①如图1，AE与BF有怎样的位置关系？请说明理由．

②如图2，连接AF、EF，如果AB＝6，那么△AEF的面积有可能等于8吗？若有可能，请求出此时BE的长；若不可能，请说明理由．

（2）如图3，G为AB边上一点，满足FG⊥AE，垂足为H，延长CD至点M，使DM＝BE，连接AM．

①求证：四边形AMFG是平行四边形．

②当AG＝4，DF＝2，∠EAB＝15°时，请直接写出正方形ABCD的边长　              　．

13．综合与实践﹣猜想、证明与拓广

问题情境：

数学课上同学们探究正方形上的动点引发的有关问题，如图1，正方形ABCD中，点E是BC边上的一点，点D关于直线AE的对称点为点F，直线DF交AB于点H，直线FB与直线AE交于点G，连接DG，CG．

猜想证明

（1）当图1中的点E与点B重合时得到图2，此时点G也与点B重合，点H与点A重合，同学们发现线段GF与GD有确定的数量关系和位置关系，其结论为：　            　；

（2）希望小组的同学发现，图1中的点E在边BC上运动时，（1）中结论始终成立，为证明这两个结论，同学们展开了讨论：

小敏：根据轴对称的性质，很容易得到直线AE是线段DF的垂直平分线…

小丽：连接AF，图中出现新的等腰三角形，如△AFB，…

小凯：不妨设图中不断变化的角∠BAF的度数为n，并设法用n表示图中的一些角，求出∠FGD的度数，从而可证明结论．

请你参考同学们的思路，完成证明：

联系拓广：

（3）如图3若将题中的“正方形ABCD”变为“菱形ABCD”，∠ABC＝α，其余条件不变，请探究∠DFG的度数，并直接写出结果（用含α的式子表示）．

14．如图，在正方形ABCD中，E为AB边上一点，连接DE，交AC于H点，过点D作DF⊥DE，交BC的延长线于F，连接EF交于AC于点G．

（1）请写出AE和CF的数量关系：　   　；

（2）求证：点G是EF的中点；

（3）若正方形ABCD的边长为4，且AE＝1，求GH•GA的值．

15．如图，E为正方形ABCD的边AB延长线上一点，DE交AC于点F，交BC于点G，H为GE的中点，求证：FB⊥BH．

16．如图，在正方形ABCD中，点E、F分别是AB、BC上的点，且AE＝BF．求证：AF⊥DE．

17．如图，正方形ABCD和正方形DEFG有公共顶点D．

（1）如图1，连接AG和CE，直接写出AG和CE的关系　            　；

（2）如图2，连接AE，M为AE中点，连接DM、CG，探究DM、CG的关系，并说明理由；

（3）如图3，若AB＝4，DE＝2，直线AG与直线CE交于点P，请直接写出AP的取值范围：　            　．

18．如图，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．

（1）求证：AM＝AD+MC；

（2）若AD＝4，求AM的长．