数学必修23.2由三视图还原成实物图同步达标检测题
展开2019-2020学年北师大版必修二 由三视图还原成实物图 课时作业
1.下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③
C.①④ D.②④
解析:选D.正方体的三视图都是正方形,不符合题意;圆锥的正视图和侧视图都是等腰三角形,俯视图是圆(包含圆心),符合题意;三棱台的正视图、侧视图和俯视图各不相同,不符合题意;正四棱锥的正视图和侧视图都是等腰三角形,俯视图是正方形(含两条对角线),符合题意.故选D.
2.下列说法正确的有( )
①两个面平行且相似,其余各面都是梯形的多面体是棱台;
②经过球面上不同的两点只能作一个大圆;
③各侧面都是正方形的四棱柱一定是正方体;
④圆锥的轴截面是等腰三角形.
A.1个 B.2个
C.3个 D.4个
解析:选A.①中若两个底面平行且相似,其余各面都是梯形,并不能保证侧棱会交于一点,所以①不正确;②中若球面上不同的两点恰为球的某条直径的两个端点,则过此两点的大圆有无数个,所以②不正确;③中底面不一定是正方形,所以③不正确;很明显④是正确的.
3.(2019·沈阳市教质量监测(一))“牟合方盖”是我国古代数家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图所示,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是( )
解析:选B.根据直观图以及图中的辅助四边形分析可知,当正视图和侧视图完全相同时,俯视图为B,故选B.
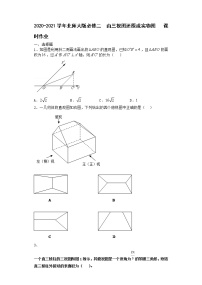
4.如图所示,在三棱台A′B′C′ABC中,沿A′BC截去三棱锥A′ABC,则剩余的部分是( )
A.三棱锥
B.四棱锥
C.三棱柱
D.组合体
解析:选B.如图所示,在三棱台A′B′C′ABC中,沿A′BC截去三棱锥A′ABC,剩余部分是四棱锥A′BCC′B′.
5.有一个长为5 cm,宽为4 cm的矩形,则其直观图的面积为________.
解析:由于该矩形的面积S=5×4=20(cm2),所以其直观图的面积S′=S=5(cm2).
答案:5 cm2
6.一个圆台上、下底面的半径分别为3 cm和8 cm,若两底面圆心的连线长为12 cm,则这个圆台的母线长为________cm.
解析:如图,过点A作AC⊥OB,交OB于点C.
在Rt△ABC中,AC=12 cm,BC=8-3=5(cm).
所以AB==13(cm).
答案:13
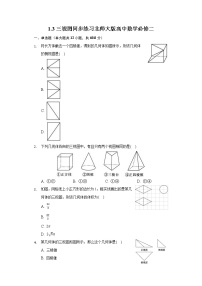
7.如图1,在四棱锥PABCD中,底面为正方形,PC与底面ABCD垂直,图2为该四棱锥的正视图和侧视图,它们是腰长为6 cm的全等的等腰直角三角形.
(1)根据所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;
(2)求PA的长.
解:(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形,如图,其面积为36 cm2.
(2)由侧视图可求得PD===6 (cm).
由正视图可知AD=6 cm,且AD⊥PD,
所以在Rt△APD中,
PA= = =6 (cm).
8.如图所示,在侧棱长为2的正三棱锥VABC中,∠AVB=∠BVC=∠CVA=40°,过A作截面AEF,求△AEF周长的最小值.
解:如图,将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,则线段AA1的长即为所求△AEF的周长的最小值.
取AA1的中点D,
连接VD,
则VD⊥AA1,∠AVD=60°.
在Rt△VAD中,
AD=VA·sin 60°=3,
所以AA1=2AD=6,
即△AEF周长的最小值为6.
[综合题组练]
1.(2019·福州市质量检测)棱长为1的正方体ABCDA1B1C1D1木块的直观图如图所示,平面α过点D且平行于平面ACD1,则该木块在平面α内的正投影面积是( )
A. B.
C. D.1
解析:选A.棱长为1的正方体ABCDA1B1C1D1木块在平面α内的正投影是三个全等的菱形(如图)正投影可以看成两个边长为的等边三角形,所以木块在平面α内的正投影面积是2××××=.
2.(2018·高考北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )
A.1 B.2
C.3 D.4
解析:选C.将三视图还原为直观图,几何体是底面为直角梯形,且一条侧棱和底面垂直的四棱锥,如图所示.
易知,BC∥AD,BC=1,AD=AB=PA=2,AB⊥AD,PA⊥平面ABCD,故△PAD,△PAB为直角三角形,
因为PA⊥平面ABCD,BC⊂平面ABCD,
所以PA⊥BC,又BC⊥AB,且PA∩AB=A,
所以BC⊥平面PAB,又PB⊂平面PAB,所以BC⊥PB,
所以△PBC为直角三角形,容易求得PC=3,CD=,PD=2,故△PCD不是直角三角形,故选C.
3.正四棱锥的底面边长为2,侧棱长均为,其正视图和侧视图是全等的等腰三角形,则正视图的周长为______________________________________________.
解析:由题意知,正视图就是如图所示的截面PEF,其中E,F分别是AD,BC的中点,连接AO,易得AO=,又PA=,于是解得PO=1,所以PE=,故其正视图的周长为2+2.
答案:2+2
4.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是________.
解析:作出直观图如图所示,通过计算可知AF、DC最长且DC=AF==3.
答案:3
5.某几何体的三视图如图所示.
(1)判断该几何体是什么几何体?
(2)画出该几何体的直观图.
解:(1)该几何体是一个正方体切掉两个圆柱后得到的几何体.
(2)直观图如图所示.
6.(综合型)如图是一个几何体的正视图和俯视图.
(1)试判断该几何体是什么几何体;
(2)画出其侧视图,并求该平面图形的面积.
解:(1)正六棱锥.
(2)其侧视图如图:
其中AB=AC,AD⊥BC,
且BC的长是俯视图中的正六边形对边的距离,
即BC=a,
AD的长是正六棱锥的高,即AD=a,
所以该平面图形的面积S=·a·a=a2.
2020-2021学年6.2垂直关系的性质课时作业: 这是一份2020-2021学年6.2垂直关系的性质课时作业,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高中数学3.2由三视图还原成实物图课时练习: 这是一份高中数学3.2由三视图还原成实物图课时练习,共3页。
北师大版必修27.3球的表面积和体积一课一练: 这是一份北师大版必修27.3球的表面积和体积一课一练,共13页。试卷主要包含了下列结论正确的是,下列几何体中为棱柱的是等内容,欢迎下载使用。