

高中数学北师大版必修32.3循环结构当堂检测题
展开十四 循 环 结 构
(20分钟·35分)
1.阅读如图所示的算法框图,运行相应的算法,输出的结果是 ( )
A.6 B.7 C.8 D.9
【解析】选C.S=2,n=1;S==-1,n=2;S==,n=4;S==2,n=8.故输出的结果为8.
2.(2019·天津高考改编)阅读算法框图,运行相应的算法,输出S的值为( )
A.5 B.8 C.24 D.29
【解析】选B.S=1,i=2→j=1,S=1+2·21=5,i=3,S=8,i=4,结束循环,故输出8.
3.执行如图所示的算法框图,如果输入的a=4,b=6,那么输出的n= ( )
A.3 B.4 C.5 D.6
【解析】选B.执行第一次循环的情况是:a=2,b=4,a=6,s=6,n=1;执行第二次循环的情况是:a=-2,b=6,a=4,s=10,n=2,执行第三次循环的情况是:a=2,b=4,a=6,s=16,n=3,执行第四次循环的情况是:a=-2,b=6,a=4,s=20,n=4.根据走出循环体的判断条件可知执行完第四次走出循环体,输出n值,n值为4.
4.执行如图所示的算法框图,若p=0.8,则输出的n=________.
【解析】第一次循环后:S=,n=2;第二次循环后:S=+=,n=3;第三次循环后:S=++=,n=4,此时循环结束.
答案:4
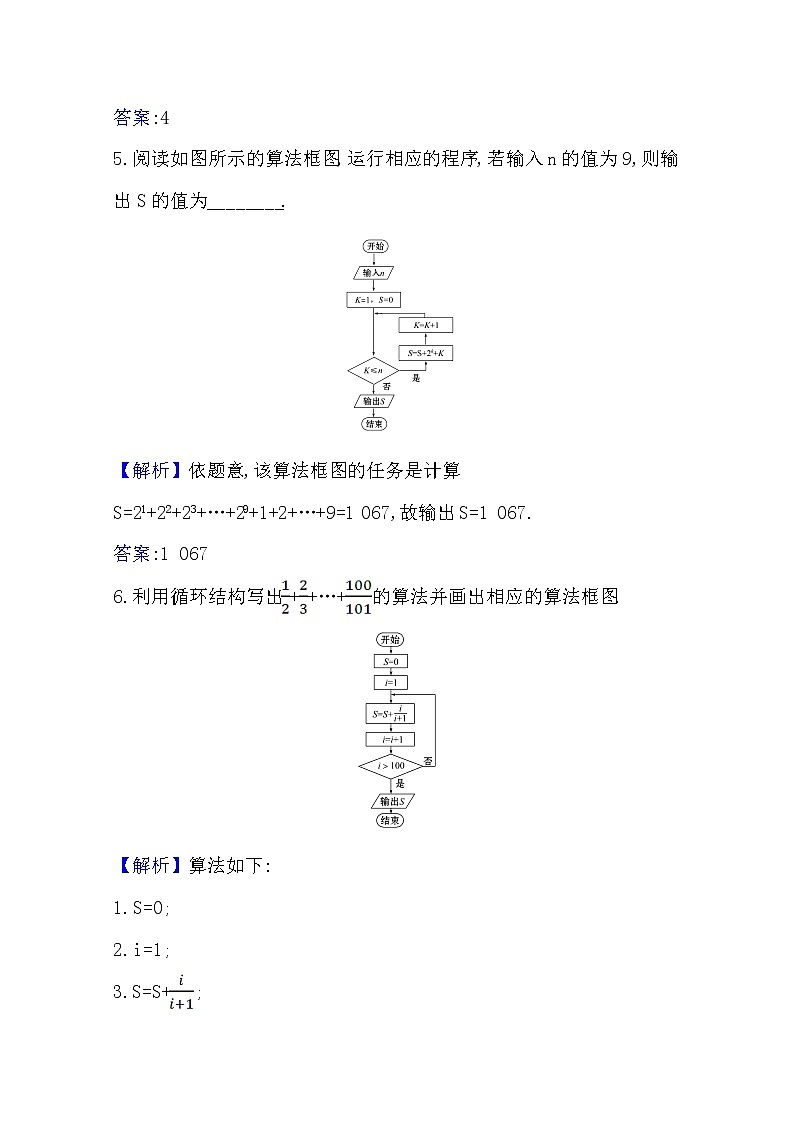
5.阅读如图所示的算法框图,运行相应的程序,若输入n的值为9,则输出S的值为________.
【解析】依题意,该算法框图的任务是计算S=21+22+23+…+29+1+2+…+9=1 067,故输出S=1 067.
答案:1 067
6.利用循环结构写出++…+的算法并画出相应的算法框图.
【解析】算法如下:
1.S=0;
2.i=1;
3.S=S+;
4.i=i+1;
5.如果i不大于100,转第3步,否则输出S.
相应算法框图如图所示:
(30分钟·60分)
一、选择题(每小题5分,共25分)
1.执行如图所示的算法框图,输出的结果为 ( )
A.(-2,2) B.(-4,0)
C.(-4,-4) D.(0,-8)
【解析】选B.x=1,y=1,k=0;
s=0,t=2;x=0,y=2,k=1;
s=-2,t=2,x=-2,y=2,k=2;
s=-4,t=0,x=-4,y=0,k=3.
输出(-4,0).
2.如图所示是计算某年级500名学生期末考试(满分为100分)及格率q的算法框图,则图中空白框内应填入 ( )
A.q= B.q=
C.q= D.q=
【解析】选D.由判断框及输出可知,M表示及格人数,N表示不及格人数,所以及格率q=.
3.如图所示算法框图的输出结果是 ( )
A.3 B.4 C.5 D.8
【解析】选B.利用循环结构求解.当x=1,y=1时,满足x≤4,则x=2,y=2;当x=2,y=2时,满足x≤4,则x=2×2=4,y=2+1=3;当x=4,y=3时,满足x≤4,则x=2×4=8,y=3+1=4;当x=8,y=4时,不满足x≤4,则输出y=4.
4.如图所示的算法框图输出的S是126,则①应为 ( )
A.n≤5 B.n≤6
C.n≤7 D.n≤8
【解析】选B.2+22+23+24+25+26=126,所以应填“n≤6”或“n<7”.
5.如图所示的算法框图,若输出k的值为6,则判断框内可填入的条件是( )
A.s> B.s> C.s> D.s>
【解析】选C.第一次循环:s=1×=,k=8;
第二次循环:s=×=,k=7;
第三次循环:s=×=,k=6,此时退出循环,输出k=6.故判断框内可填s>.
二、填空题(每小题5分,共15分)
6.执行如图所示的算法框图,若输入的x的值为1,则输出的y的值为________.
【解析】执行算法为x=1→x=2,y=3×22+1=13.
答案:13
7.如图所示,算法框图中输出S的值为________.
【解析】该算法框图的运行过程是:i=1,S=1,
i=1+1=2,
S=2×(1+1)=4,
i=2>5不成立;
i=2+1=3,
S=2×(4+1)=10,
i=3>5不成立;
i=3+1=4,
S=2×(10+1)=22,
i=4>5不成立;
i=4+1=5,
S=2×(22+1)=46,
i=5>5不成立;
i=5+1=6,
S=2×(46+1)=94,
i=6>5成立,输出S=94.
答案:94
8.美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人长于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.其算法框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,则输出结果为________.
【解析】由算法框图可以看出,当输入a=8,n=2,ξ=0.5时,m=4,n=3,|m-n|>0.5,继续执行循环,m=,n=,|m-n|<0.5,退出循环,输出n=.
答案:
三、解答题(每小题10分,共20分)
9.设计一个算法,求1×22×33×…×100100的值,并画出算法框图.
【解析】(答案不唯一)算法步骤如下:
1.S=1;
2.i=1;
3.S=S×ii;
4.i=i+1;
5.判断i>100是否成立,若成立,则输出S,结束算法;否则,返回第3步.
算法框图如图所示:
10.经过市场调查分析得知,2019年第一季度内,北京市海淀区居民对某种商品的需求量为18 000件.为保证商品不脱销,商家在月初时将商品按相同数量投放市场.已知年初商品的库存量为50 000件,用K表示商品的库存量,请设计一个算法框图,求出第一季度结束时商品的库存量.
【解析】设置出判断框中的条件,再由第一季度每个月份结束时商品的库存量,确定判断框的“是”与“否”分支对应的操作,由此即可画出算法框图,用循环结构实现这一算法.算法框图如图:
1.考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则乘3再加1;如果它是偶数,则除以2.如此循环,最终都能得到1.阅读如图所示的算法框图,运行相应的算法,输出的结果i= ( )
A.4 B.5 C.6 D.7
【解析】选D.a=10,a=5,i=2;
a=16,i=3;
a=8,i=4;
a=4,i=5;
a=2,i=6;
a=1,i=7;
当a=1时满足退出循环的条件,故输出结果为7.
2.数学课上,老师为了提高同学们的兴趣,先让同学们从1到3循环报数,结果最后一个同学报2;再让同学们从1到5循环报数,最后一个同学报3;又让同学们从1到7循环报数,最后一个同学报4.请你设计一个算法,计算这个班至少有多少人,并画出算法框图.
【解析】算法如下:1.选择一个起始数x=7.
2.判断这个数是否满足除以3余2.如果不满足,则加1后再判断,直至满足,转入第3步.
3.判断第2步得到的数是否满足除以5余3.如果不满足,则加1后再转入第2步判断,直至满足,转入第4步.
4.判断第3步得到的数是否满足除以7余4.如果不满足,则加1后再转入第2步判断,直至满足,转入第5步.
5.输出第4步得到的数,即为所求的最小值.
算法框图如图所示:
关闭Word文档返回原板块
北师大版必修32.2建立概率模型达标测试: 这是一份北师大版必修32.2建立概率模型达标测试,共12页。
北师大版必修31.1频率与概率课时练习: 这是一份北师大版必修31.1频率与概率课时练习,共9页。试卷主要包含了下列说法,45B,已知随机事件A发生的频率是0,从100个同类产品中任取3个,7%×600=472等内容,欢迎下载使用。
高中数学北师大版必修32.3循环结构课后练习题: 这是一份高中数学北师大版必修32.3循环结构课后练习题,共9页。试卷主要包含了3 循环结构等内容,欢迎下载使用。













