

所属成套资源:高考数学(理)一轮复习课时作业含解析北师大版专题
高考数学一轮复习第六章第二节二元一次不等式组与简单的线性规划问题课时作业理含解析北师大版
展开
这是一份高考数学一轮复习第六章第二节二元一次不等式组与简单的线性规划问题课时作业理含解析北师大版,共9页。
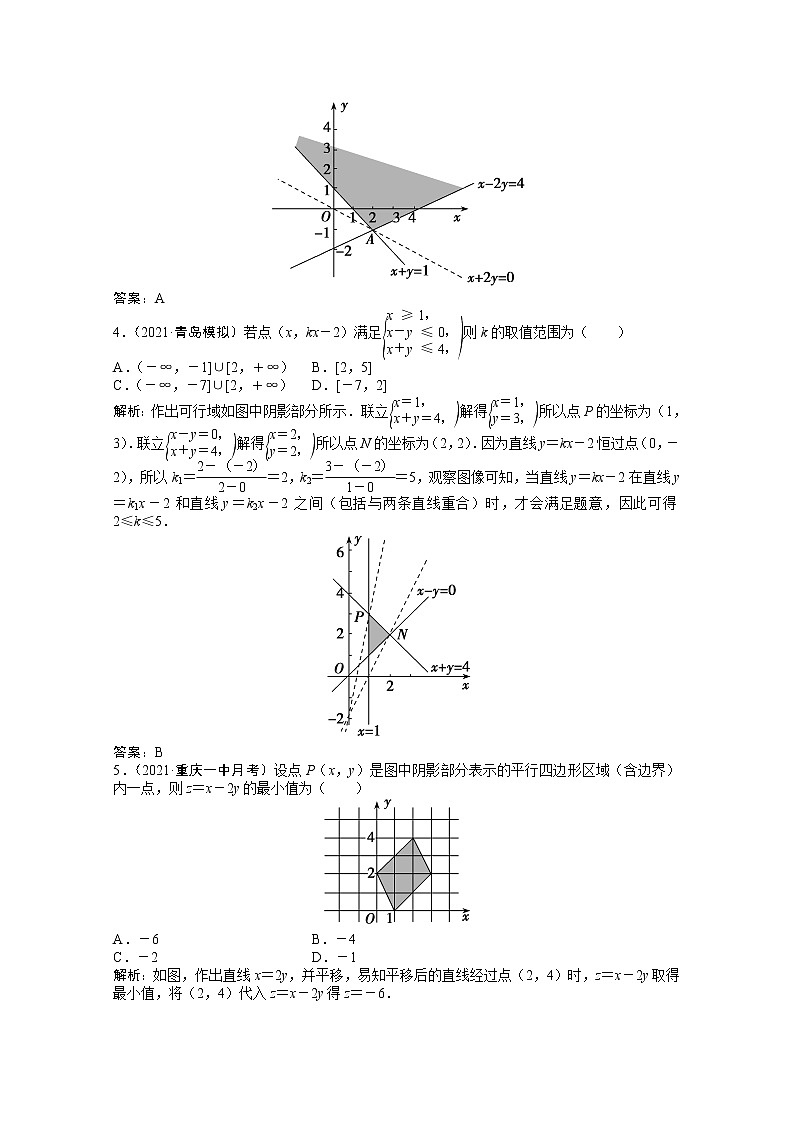
第二节 二元一次不等式(组)与简单的线性规划问题授课提示:对应学生用书第333页[A组 基础保分练]1.(2021·临汾模拟)不等式y(x+y-2)≥0在平面直角坐标系中表示的区域(用阴影部分表示)是( )解析:由y·(x+y-2)≥0,得或所以不等式y·(x+y-2)≥0在平面直角坐标系中表示的区域是C项.答案:C2.设x,y满足约束条件则z=x+y的最大值是( )A.-15 B.-9C.1 D.9解析:作出不等式组表示的平面区域如图中阴影部分所示,∵z=x+y,∴y=-x+z,作出直线y=-x,平移该直线,当直线过A(0,1)时,z取得最大值,zmax=1.答案:C3.(2021·西安模拟)不等式组的解集记为D,若任意(x,y)∈D,则( )A.x+2y≥-2 B.x+2y≥2C.x-2y≥-2 D.x-2y≥2解析:作出不等式组表示的平面区域如图中阴影部分所示.设z=x+2y,作出直线l0:x+2y=0,易知z的最小值为0,无最大值.所以根据题意知,任意(x,y)∈D,x+2y≥0恒成立,故x+2y≥-2恒成立.答案:A4.(2021·青岛模拟)若点(x,kx-2)满足则k的取值范围为( )A.(-∞,-1]∪[2,+∞) B.[2,5]C.(-∞,-7]∪[2,+∞) D.[-7,2]解析:作出可行域如图中阴影部分所示.联立解得所以点P的坐标为(1,3).联立解得所以点N的坐标为(2,2).因为直线y=kx-2恒过点(0,-2),所以k1==2,k2==5,观察图像可知,当直线y=kx-2在直线y=k1x-2和直线y=k2x-2之间(包括与两条直线重合)时,才会满足题意,因此可得2≤k≤5.答案:B5.(2021·重庆一中月考)设点P(x,y)是图中阴影部分表示的平行四边形区域(含边界)内一点,则z=x-2y的最小值为( )A.-6 B.-4C.-2 D.-1解析:如图,作出直线x=2y,并平移,易知平移后的直线经过点(2,4)时,z=x-2y取得最小值,将(2,4)代入z=x-2y得z=-6.答案:A6.变量x,y满足约束条件则(x-2)2+y2的最小值为( )A. B.C. D.5解析:不等式组表示的平面区域如图中的阴影部分所示.设P(x,y)是该区域内的任意一点,则(x-2)2+y2的几何意义是点P(x,y)与点M(2,0)距离的平方.由图可知,当点P的坐标为(0,1)时,|PM|最小,所以|PM|≥=,所以|PM|2≥5,即(x-2)2+y2≥5.答案:D7.设x,y满足约束条件则目标函数z=的取值范围是________.解析:画出约束条件所表示的平面区域,如图阴影部分所示.将目标函数z=看成是区域内的点(x,y)与定点D(2,0)连线的斜率.由图可知,斜率最大为kBD=,斜率最小为kAD=-,所以目标函数z=的取值范围为.答案:8.已知x,y满足条件则的取值范围是________.解析:画出不等式组表示的可行域,如图中阴影部分所示,=1+2×,表示可行域中的点(x,y)与点P(-1,-1)连线的斜率.由图可知,当x=0,y=3时,取得最大值,且=9.因为点P(-1,-1)在直线y=x上,所以当点(x,y)在线段AO上时,取得最小值,且=3.所以的取值范围是[3,9].答案:[3,9]9.若x,y满足约束条件(1)求目标函数z=x-y+的最值;(2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围.解析:(1)作出可行域如图阴影部分所示,可求得A(3,4),B(0,1),C(1,0).平移初始直线x-y=0,当其过A(3,4)时,z取最小值-2,过C(1,0)时,z取最大值1.∴z的最大值为1,最小值为-2.(2)z=ax+2y仅在点C(1,0)处取得最小值,由图像可知-1<-<2,解得-4<a<2.故所求a的取值范围是(-4,2).[B组 能力提升练]1.(2021·漳州模拟)若实数x,y满足约束条件则x+y( )A.有最小值无最大值B.有最大值无最小值C.既有最小值也有最大值D.既无最小值也无最大值解析:如图中阴影部分所示即为实数x,y满足的可行域,由得A.由图易得当x=,y=时,x+y有最小值,没有最大值.答案:A2.若平面区域夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是( )A. B.C. D.解析:作出平面区域如图所示:∴当直线y=x+b分别经过A,B时,平行线间的距离最小.联立方程组解得A(2,1),联立方程组解得B(1,2).两条平行线分别为y=x-1,y=x+1,即x-y-1=0,x-y+1=0,∴平行线间的距离为d==.答案:D3.不等式组表示的平面区域为Ω,直线y=kx-1与区域Ω有公共点,则实数k的取值范围为( )A.(0,3] B.[-1,1]C.(-∞,3] D.[3,+∞)解析:直线y=kx-1过定点M(0,-1),由图可知,当直线y=kx-1经过直线y=x+1与直线x+y=3的交点C(1,2)时,k最小,此时kCM==3,因此k≥3,即k∈[3,+∞).答案:D4.实数x,y满足(a<1),且z=2x+y的最大值是最小值的4倍,则a的值是( )A. B.C. D.解析:在直角坐标系中作出不等式组所表示的可行域如图中阴影部分(包括边界)所示,当目标函数z=2x+y经过可行域中的点B(1,1)时有最大值3,当目标函数z=2x+y经过可行域中的点A(a,a)时有最小值3a,由3=4×3a,得a=.答案:B5.已知实数x,y满足则z=|x-y+1|的取值范围是________.解析:作出可行域如图中阴影部分所示,作出直线x-y+1=0,因为z=|x-y+1|=×表示点(x,y)到直线x-y+1=0的距离的倍,所以结合图像易知0≤z≤3.答案:[0,3]6.(2021·南昌高三调研)若关于x,y的不等式组表示的平面区域是一个三角形,则k的取值范围是________.解析:不等式|x|+|y|≤2表示的平面区域为如图所示的正方形ABCD及其内部.直线y+2=k(x+1)过定点P(-1,-2),斜率为k,要使平面区域表示一个三角形,则kPD<k≤kPA或k<kPC.而kPD=0,kPA==,kPC==-2,故0<k≤或k<-2.答案:(-∞,-2)∪7.某共享汽车品牌在某市投放1 500辆宝马轿车,为人们的出行提供了一种新的交通方式.该市的市民小王喜欢自驾游,他在该市通过网络组织了一场“周日租车游”活动,招募了30名自驾游爱好者租车旅游,他们计划租用A,B两种型号的宝马轿车,已知A,B两种型号的宝马轿车每辆的载客量都是5人,每天的租金分别为600元/辆和1 000元/辆,根据要求租车总数不超过12辆且不少于6辆,且A,B两种型号的轿车至少各租用1辆,求租车所需的租金最少为多少元.解析:设分别租用A,B两种型号的轿车x辆,y辆,所需的总租金为z元,则z=600x+1 000y,其中x,y满足不等式组作出不等式组所表示的可行域如图中阴影部分所示,目标函数可化为y=-x+,由图可知当直线y=-x+过点C时,目标函数z取得最小值.由解得C(5,1).所以总租金z的最小值为600×5+1 000×1=4 000(元).[C组 创新应用练]1.设p:实数x,y满足(x-1)2+(y-1)2≤2,q:实数x,y满足则p是q的( )A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件解析:画出可行域,易知命题q中不等式组表示的平面区域在命题p中不等式表示的圆面内,故是必要不充分条件.答案:A2.记不等式组表示的平面区域为Ω,点P的坐标为(x,y),则下面四个命题,p1:任意P∈Ω,y≤0,p2:任意P∈Ω,x-y≥2,p3:任意P∈Ω,-6≤y≤,p4:存在P∈Ω,x-y=.其中是真命题的是( )A.p1,p2 B.p1,p3C.p2,p4 D.p3,p4解析:作出平面区域Ω,如图中阴影部分所示,其中A(4,0),由图可知,y∈(-∞,0].作出直线y=x,并平移,易知当平移后的直线经过点A时,x-y取得最小值2,则x-y≥2,从而p1,p2是真命题.答案:A
相关试卷
这是一份高考数学一轮复习第十章第二节随机抽样课时作业理含解析北师大版,共4页。
这是一份高考数学一轮复习第六章第四节推理与证明课时作业理含解析北师大版,共6页。
这是一份高考数学一轮复习第六章第二节二元一次不等式组与简单的线性规划问题课时作业理含解析北师大版,共9页。









