高考数学一轮复习练44第七章立体几何第四讲直线平面平行的判定与性质含解析新人教版

这是一份高考数学一轮复习练44第七章立体几何第四讲直线平面平行的判定与性质含解析新人教版，共10页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
第四讲　直线、平面平行的判定与性质
A组基础巩固
一、单选题
1．(2021·河南郑州、商丘名师联盟联考)过平面α外的直线l，作一组平面与α相交，若所得交线为a，b，c，…，则这些交线的位置关系为(　A　)
A．平行或交于同一点　　 B．相交于同一点
C．相交但交于不同的点　　 D．平行
[解析]　若l∥α，则l∥a，l∥b，l∥c，…，∴a∥b∥c….若l∩α＝P，则a，b，c，…交于点P.
2．(2021·辽宁沈阳东北育才学校模拟)在空间中，下列命题中为真命题的是(　D　)
A．垂直于同一直线的两条直线平行
B．平行于同一平面的两条直线平行
C．垂直于同一平面的两个平面平行
D．平行于同一平面的两个平面平行
3．(2021·黑龙江大庆让胡路区联考)已知m，n是直线，α是平面，且m∥α，则下列结论中正确的是(　B　)
A．∀n⊂α，都有m∥n
B．∃n⊂α，使m⊥n
C．∀n∥m，都有n∥α
D．∃n⊥α，使m∥n
[解析]　由m，n是直线，α是平面，且m∥α，得：对于A，∀n⊂α，则m，n平行或异面，故A不正确；对于B，∃n⊂α，使m⊥n，故B正确；对于C，∀n∥m，则n∥α或n⊂α，故C不正确；对于D，若n⊥α，因为m∥α，所以m⊥n，故D不正确，故选B.
4．(2021·湖北武汉模拟)设α、β、γ为平面，a、b为直线，给出下列条件：
①a⊂α，b⊂β，a∥β，b∥α；
②α∥γ，β∥γ；
③α⊥γ，β⊥γ；
④a⊥α，b⊥β，a∥b
其中能推出α∥β的条件是(　C　)
A．①②　　 B．②③　　
C．②④　　 D．③④
[解析]　①有如下反例：

故，不能推出α∥β；
②面面平行的判定：平行于同一个平面的两个平面平行，能推出α∥β；
③有如下反例：

故，不能推出α∥β；
④面面平行的推论：如果两个平面的垂线平行，那么这两个平面平行，能推出α∥β.故选：C．
5．(2021·山东泰安期末)有两条不同的直线m，n与两个不同的平面α，β，下列命题正确的是(　A　)
A．m⊥α，n∥β，且α∥β，则m⊥n
B．m⊥α，n⊥β，且α⊥β，则m∥n
C．m∥α，n⊥β，且α⊥β，则m∥n
D．m∥α，n∥β，且α∥β，则m∥n
[解析]　对于A，由m⊥α，n∥β，且α∥β得m⊥n，故正确；对于B，由m⊥α，n⊥β，α⊥β得m⊥n，故错误；对于C，由m∥α，n⊥β，且α⊥β得m∥n或m，n相交或异面，故错误；对于D，由m∥α，n∥β，且α∥β得m，n的关系可以是相交或平行或异面，故错误．故选A.
6．若P为异面直线a，b外一点，则过P且与a，b均平行的平面(　B　)
A．不存在　　 B．零个或一个
C．可以有两个　　 D．有无数多个
[解析]　记a与P所确定的平面为α，当b∥α时，与a，b均平行的平面不存在，当b不平行α时，与a，b均平行的平面有一个，故选B.
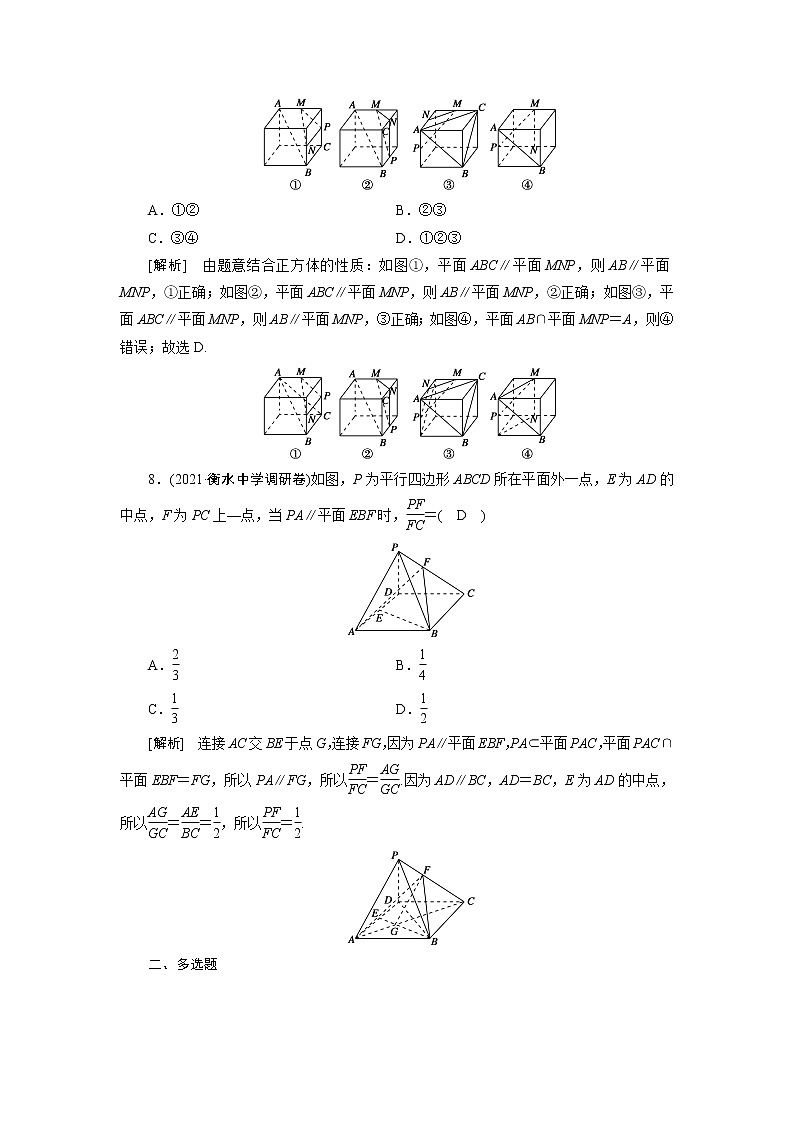
7．(2021·湖南省长沙市长郡中学月考)如图所示的四个正方体中，A，B分别为正方体的两个顶点，M，N，P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号为(　D　)

A．①②　　 B．②③
C．③④　　 D．①②③
[解析]　由题意结合正方体的性质：如图①，平面ABC∥平面MNP，则AB∥平面MNP，①正确；如图②，平面ABC∥平面MNP，则AB∥平面MNP，②正确；如图③，平面ABC∥平面MNP，则AB∥平面MNP，③正确；如图④，平面AB∩平面MNP＝A，则④错误；故选D.

8．(2021·衡水中学调研卷)如图，P为平行四边形ABCD所在平面外一点，E为AD的中点，F为PC上—点，当PA∥平面EBF时，＝(　D　)

A．　　 B．　　
C．　　 D．
[解析]　连接AC交BE于点G，连接FG，因为PA∥平面EBF，PA⊂平面PAC，平面PAC∩平面EBF＝FG，所以PA∥FG，所以＝.因为AD∥BC，AD＝BC，E为AD的中点，所以＝＝，所以＝.

二、多选题

9．(2021·辽宁省测评)如图，在三棱柱ABC－A1B1C1中，底面ABC是等边三角形，侧棱AA1⊥底面ABC，D为AB的中点，若AB＝2，AA1＝，则(　AC　)
A．CD⊥A1D
B．异面直线A1D与AC1所成角的余弦值为
C．异面直线A1D与AC1所成角的余弦值为
D．CD∥平面AB1C1
[解析]　易知CD⊥平面ABB1A1，∴CD⊥A1D，所以A项正确；若CD∥平面AB1C1，又BC∥B1C1，显然BC∥平面AB1C1，∴平面BCD∥平面AB1C1，这显然不成立，所以D项不正确；过点A在平面ABB1A1内作直线A1D的平行线交B1A1的延长线于点D1，连接C1D1，易知异面直线A1D与AC1所成的角等于∠D1AC1，在△D1AC1中，可知D1A＝D1C1＝，AC1＝，所以异面直线A1D与AC1所成角的余弦值为＝＝.所以C项正确．
10．(2021·山东乐陵一中模拟)在正方体ABCD－A1B1C1D1中，下列直线或平面与平面ACD1平行的有(　AD　)
A．直线A1B　　 B．直线BB1
C．平面A1DC1　　 D．平面A1BC1
[解析]　如图，

A1B∥D1C，又A1B⊄平面ACD1，
∴A1B∥平面ACD1，A正确；
BB1与平面ACD1相交，B错误；
DC1与CD1相交，∴平面ACD1与平面A1DC1相交，C错误；∵A1C1∥AC，A1C1⊄平面ACD1，
∴A1C1∥平面ACD1，又A1B∩A1C1＝A，
∴平面ACD1∥平面A1BC1，D正确；
故选AD.
11．(2021·安徽安庆模拟改编)在正方体ABCD－A1B1C1D1中，M、N、Q分别是棱D1C1，A1D1、BC的中点，点P在BD1上且BP＝BD1，则下列说法中正确的是(　BC　)
A．MN∥平面APC　　 B．C1Q∥平面APC
C．A、P、M三点共线　　 D．平面MNQ∥平面APC
[解析]　对于A.连接MN，AC，则MN∥AC，连接AM、CN，

易得AM、CN交于点P，即MN⊂平面APC，
所以MN∥平面APC是错误的；
对于B.由A知M、N在平面APC内，由题易知AN∥C1Q，
所以C1Q∥平面APC是正确的；
对于C．由A知，A，P，M三点共线是正确的；
对于D.由A知MN⊂平面APC，又MN⊂平面MNQ，
所以平面MNQ∥平面APC是错误的．故选B、C．
三、填空题
12．(2021·桂林二模)已知a，b，c为三条不重合的直线，α，β为两个不重合的平面，给出下列四个命题：①a∥b，b∥c⇒a∥c；②a∥α，b∥α⇒a∥b；③a∥α，β∥α⇒a∥β；④a⊄α，b⊂α，a∥b⇒a∥α.其中正确的命题是 ①④ .(写出所有正确命题的序号)
[解析]　根据线线平行的传递性，可知①正确；若a∥α，b∥α，则a，b可能平行、相交、异面，故②不正确；若a∥α，β∥α，则a∥β或a⊂β，故③不正确；由线面平行的判定定理可知④正确．故正确的命题是①④.
13．已知平面α∥β，点A，C∈α，B，D∈β，直线AB与直线CD交于点S，且AS＝8，BS＝9，CD＝34，则CS的长为 16或272 .
[解析]　本题主要考查两平面平行的性质定理．①当点S在两平行平面之间时，如图1所示，∵直线AB与直线CD交于点S，直线AB与直线CD可确定一个平面γ，且α∩γ＝AC，β∩γ＝BD.∵α∥β，∴AC∥BD，∴＝，即＝，得＝，解得CS＝16.②当点S在两平行平面的同侧时，如图2所示，由①知AC∥BD，则有＝，即＝，解得CS＝272.

14.如图所示，在正四棱柱ABCD－A1B1C1D1中，E，F，G，H分别是棱CC1，C1D1，D1D，DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M只需满足条件 点M在线段FH上(或点M与点H重合) 时，就有MN∥平面B1BDD1.(注：请填上你认为正确的一个条件即可，不必考虑全部可能情况)

[解析]　连接HN，FH，FN，则FH∥DD1，HN∥BD，
∴平面FHN∥平面B1BDD1，只需M∈FH，
则MN⊂平面FHN，∴MN∥平面B1BDD1.
四、解答题
15．(2021·浙江模拟)如图，四边形ABCD与ADEF均为平行四边形，M，N，G分别是AB，AD，EF的中点．
(1)求证：BE∥平面DMF；
(2)求证：平面BDE∥平面MNG.

[解析]　(1)如图，连接AE，则AE必过DF与GN的交点O，
连接MO，则MO为△ABE的中位线，所以BE∥MO，
又BE⊄平面DMF，MO⊂平面DMF，所以BE∥平面DMF.
(2)因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥GN，
又DE⊄平面MNG，GN⊂平面MNG，所以DE∥平面MNG.
又M为AB中点，所以MN为△ABD的中位线，
所以BD∥MN，
又BD⊄平面MNG，MN⊂平面MNG，所以BD∥平面MNG，
又DE与BD为平面BDE内的两条相交直线，
所以平面BDE∥平面MNG.

B组能力提升
1．设α、β、γ是三个互不重合的平面，m、n为两条不同的直线．给出下列命题：
①若n∥m，m⊂α，则n∥α；
②若α∥β，n⊄β，n∥α，则n∥β；
③若β⊥α，γ⊥α，则β∥γ；
④若n∥m，n⊥α，m⊥β，则α∥β.
其中真命题是(　C　)
A．①和②　　 B．①和③　　
C．②和④　　 D．③和④
[解析]　若n∥m，m⊂α，则n∥α或n⊂α，即命题①不正确，排除A、B；若α∥β，n⊄β，n∥α，则n∥β，则命题②正确，排除D，故应选C．
2．(2021·甘肃兰州诊断)已知直线m，n和平面α，则m∥n的一个必要条件是(　D　)
A．m∥α，n∥α　　 B．m⊥α，n⊥α
C．m∥α，n⊂α　　 D．m，n与平面α成等角
[解析]　A中，m，n可以都和平面垂直，必要性不成立；B中，m，n可以都和平面平行，必要性不成立；C中，n不一定在平面内，必要性不成立；D中，m，n平行，则m，n与α成的角一定相等，但反之如果两直线m，n与α成的角相等则不一定平行，所以是必要不充分条件，故选D.

3．(多选题)(2021·宜昌调研)如图，在棱长均相等的四棱锥P－ABCD中，O为底面正方形的中心，M，N分别为侧棱PA，PB的中点，则下列结论正确的是(　ABC　)
A．PC∥平面OMN
B．平面PCD∥平面OMN
C．OM⊥PA
D．直线PD与MN所成角的大小为90°
[解析]　

如图，连接AC，易得PC∥OM，所以PC∥平面OMN，结论A正确．同理PD∥ON，所以平面PCD∥平面OMN，结论B正确．由于四棱锥的棱长均相等，所以AB2＋BC2＝PA2＋PC2＝AC2，所以PC⊥PA，又PC∥OM，所以OM⊥PA，结论C正确．由于M，N分别为侧棱PA，PB的中点，所以MN∥AB，又四边形ABCD为正方形，所以AB∥CD，又三角形PDC为等边三角形，所以∠PDC＝60°，所以直线PD与MN所成的角即∠PDC，故D错误．故正确的结论为A、B、C．
4. (2021·江西景德镇一中月考改编)如图，在棱长为1的正方体ABCD－A1B1C1D1中，M，N分别是A1D1，A1B1的中点，过直线BD的平面α∥平面AMN，则平面α截该正方体所得截面的面积为(　B　)

A．　　 B．　　
C．　　 D．
[解析]　

如图1，取B1C1的中点E，C1D1的中点F，连接EF，BE，DF，B1D1，则EF∥B1D1，B1D1∥BD，所以EF∥BD，故EF，BD在同一平面内，连接ME，因为M，E分别为A1D1，B1C1的中点，所以ME∥AB，且ME＝AB，所以四边形ABEM是平行四边形，
所以AM∥BE，又因为BE⊂平面BDFE，AM⊄平面BDFE.
所以AM∥平面BDFE，同理AN∥平面BDFE，因为AM∩AN＝A，
所以平面AMN∥平面BDFE，所以平面BDFE为平面α，
BD＝，EF＝B1D1＝，DF＝BE＝，
等腰梯形BDFE如图2，

过E，F作BD的垂线，则四边形EFGH为矩形，
∴FG＝＝＝，
故所得截面的面积为××＝，故选B.
5．(1)如图，三棱柱A1B1C1－ABC中，点M是A1B1的中点．求证：B1C∥平面AC1M.

(2)如图，在多面体ABCDEF中，四边形ABCD是正方形，BF⊥平面ABCD，DE⊥平面ABCD，BF＝DE，M为棱AE的中点．

求证：平面BDM∥平面EFC．
[证明]　(1)在直三棱柱A1B1C1－ABC中，
侧面ACC1A1为矩形，
连接A1C，交AC1于O，

则O为A1C的中点，连接MO，
又M为A1B1的中点，∴OM∥B1C，
∵OM⊂平面AC1M，B1C⊄平面AC1M，
∴B1C∥平面AC1M.
(2)如图，连AC，设AC与BD交于点N，

则N为AC的中点，连接MN，
又M为棱AE的中点，
∴MN∥EC．
∵MN⊄平面EFC，
EC⊂平面EFC，
∴MN∥平面EFC．
∵BF⊥平面ABCD，DE⊥平面ABCD，且BF＝DE，
∴BF∥DE且BF＝DF，
∴四边形BDEF为平行四边形，∴BD∥EF.
∵BD⊄平面EFC，EF⊂平面EFC，∴BD∥平面EFC．
又MN∩BD＝N，MN，BD⊂平面BDM，
∴平面BDM∥平面EFC．