
所属成套资源:高考数学(理)一轮复习课时作业含解析北师大版专题
高考数学一轮复习第十章第三节用样本估计总体课时作业理含解析北师大版
展开这是一份高考数学一轮复习第十章第三节用样本估计总体课时作业理含解析北师大版,共7页。
用样本估计总体
授课提示:对应学生用书第395页
[A组 基础保分练]
1.(2021·广东惠州一调)已知数据x1,x2,…,x10,2的平均值为2,方差为1,则数据x1,x2,…,x10相对于原数据( )
A.一样稳定 B.变得稳定
C.变得不稳定 D.稳定性不可以判断
解析:数据x1,x2,…,x10,2的平均值为2,方差为1,故[(x1-2)2+(x2-2)2+…+(x10-2)2+(2-2)2]=1,数据x1,x2,…,x10的方差s2=[(x1-2)2+(x2-2)2+…+(x10-2)2]>1,故相对于原数据变得不稳定.
答案:C
2.样本中共有五个个体,其值分别为0,1,2,3,m.若该样本的平均值为1,则其方差为( )
A. B.
C. D.2
解析:依题意得m=5×1-(0+1+2+3)=-1,样本方差s2=(12+02+12+22+22)=2,即所求的样本方差为2.
答案:D
3.在如图所示一组数据的茎叶图中,有一个数字被污染后模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )
A.1 B.2
C.3 D.4
解析:由题图可知该组数据的极差为48-20=28,则该组数据的中位数为61-28=33,易得被污染的数字为2.
答案:B
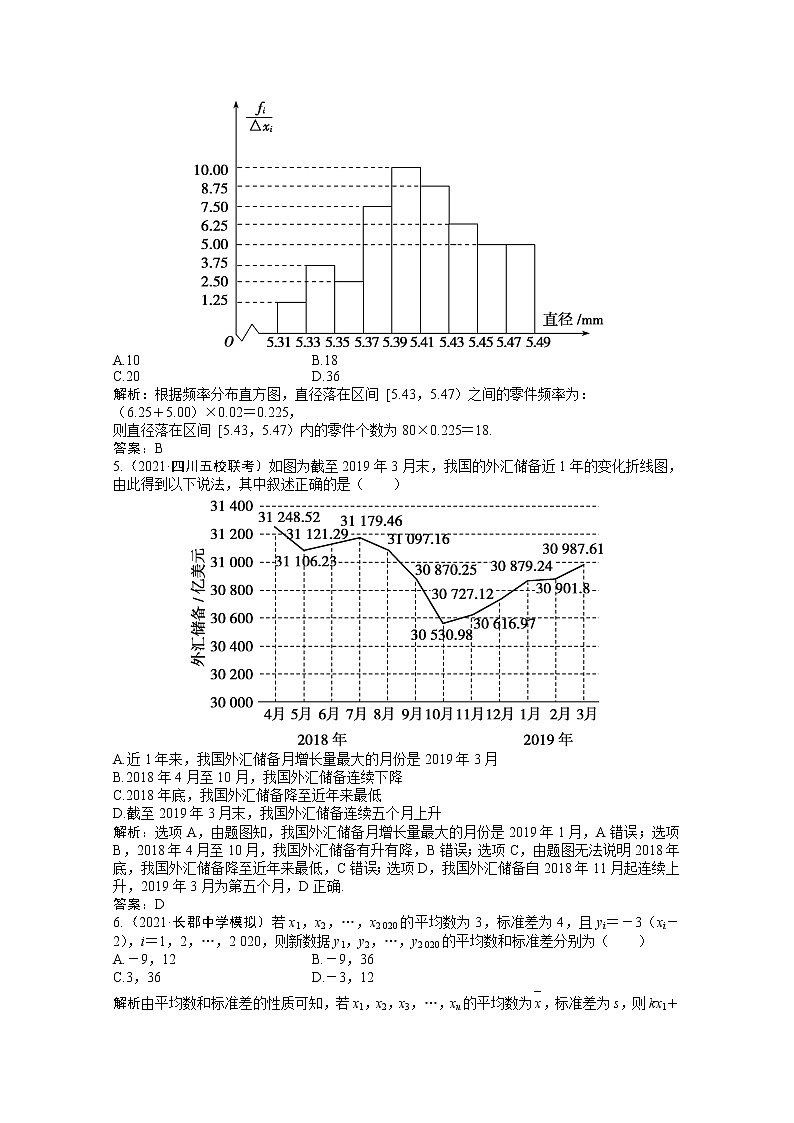
4.(2020·高考天津卷)从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组: [5.31,5.33), [5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间 [5.43,5.47)内的个数为( )
A.10 B.18
C.20 D.36
解析:根据频率分布直方图,直径落在区间 [5.43,5.47)之间的零件频率为:
(6.25+5.00)×0.02=0.225,
则直径落在区间 [5.43,5.47)内的零件个数为80×0.225=18.
答案:B
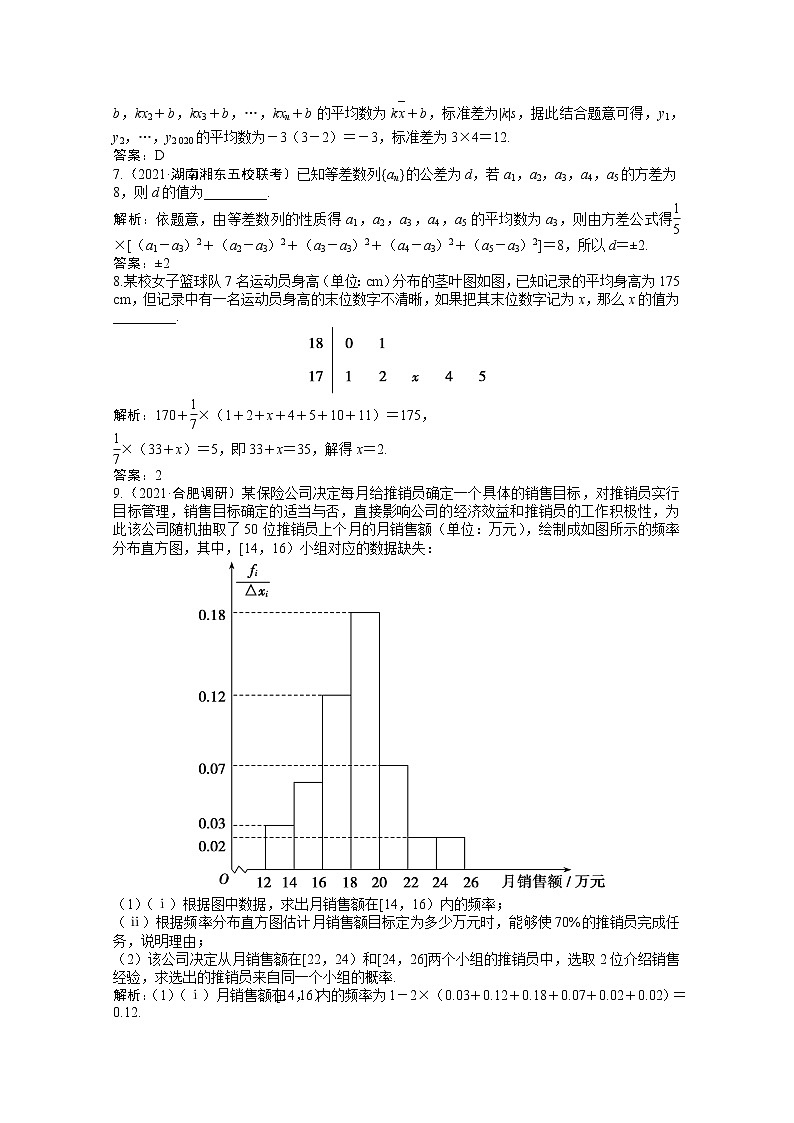
5.(2021·四川五校联考)如图为截至2019年3月末,我国的外汇储备近1年的变化折线图,由此得到以下说法,其中叙述正确的是( )
A.近1年来,我国外汇储备月增长量最大的月份是2019年3月
B.2018年4月至10月,我国外汇储备连续下降
C.2018年底,我国外汇储备降至近年来最低
D.截至2019年3月末,我国外汇储备连续五个月上升
解析:选项A,由题图知,我国外汇储备月增长量最大的月份是2019年1月,A错误;选项B,2018年4月至10月,我国外汇储备有升有降,B错误;选项C,由题图无法说明2018年底,我国外汇储备降至近年来最低,C错误;选项D,我国外汇储备自2018年11月起连续上升,2019年3月为第五个月,D正确.
答案:D
6.(2021·长郡中学模拟)若x1,x2,…,x2 020的平均数为3,标准差为4,且yi=-3(xi-2),i=1,2,…,2 020,则新数据y1,y2,…,y2 020的平均数和标准差分别为( )
A.-9,12 B.-9,36
C.3,36 D.-3,12
解析:由平均数和标准差的性质可知,若x1,x2,x3,…,xn的平均数为,标准差为s,则kx1+b,kx2+b,kx3+b,…,kxn+b的平均数为k+b,标准差为|k|s,据此结合题意可得,y1,y2,…,y2 020的平均数为-3(3-2)=-3,标准差为3×4=12.
答案:D
7.(2021·湖南湘东五校联考)已知等差数列{an}的公差为d,若a1,a2,a3,a4,a5的方差为8,则d的值为_________.
解析:依题意,由等差数列的性质得a1,a2,a3,a4,a5的平均数为a3,则由方差公式得×[(a1-a3)2+(a2-a3)2+(a3-a3)2+(a4-a3)2+(a5-a3)2]=8,所以d=±2.
答案:±2
8.某校女子篮球队7名运动员身高(单位:cm)分布的茎叶图如图,已知记录的平均身高为175 cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末位数字记为x,那么x的值为_________.
解析:170+×(1+2+x+4+5+10+11)=175,
×(33+x)=5,即33+x=35,解得x=2.
答案:2
9.(2021·合肥调研)某保险公司决定每月给推销员确定一个具体的销售目标,对推销员实行目标管理,销售目标确定的适当与否,直接影响公司的经济效益和推销员的工作积极性,为此该公司随机抽取了50位推销员上个月的月销售额(单位:万元),绘制成如图所示的频率分布直方图,其中,[14,16)小组对应的数据缺失:
(1)(ⅰ)根据图中数据,求出月销售额在[14,16)内的频率;
(ⅱ)根据频率分布直方图估计月销售额目标定为多少万元时,能够使70%的推销员完成任务,说明理由;
(2)该公司决定从月销售额在[22,24)和[24,26]两个小组的推销员中,选取2位介绍销售经验,求选出的推销员来自同一个小组的概率.
解析:(1)(ⅰ)月销售额在[14,16)内的频率为1-2×(0.03+0.12+0.18+0.07+0.02+0.02)=0.12.
(ⅱ)若70%的推销员能完成月销售额目标,则意味着30%的推销员不能完成该目标,根据频率分布直方图知,[12,14)和[14,16)两组的频率之和为0.18,故估计月销售额目标应定为16+=17(万元).
(2)根据频率分布直方图可知,[22,24)和[24,26]两组的频率之和为0.08,由50×0.08=4可知待选的推销员一共有4人,设这4人分别为A1,A2,B1,B2,则不同的选择有{A1,A2},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{B1,B2},一共6种情况,每一种情况都是等可能的,而2人来自同一组的情况有2种,故选出的推销员来自同一个小组的概率为P==.
[B组 能力提升练]
1.某位教师2020年的家庭总收入为80 000元,各种用途占比统计如下面的折线图.2021年收入的各种用途占比统计如下面的条形图,已知2021年的就医费用比2017年增加了4 750元,则该教师2021年的家庭总收入为( )
A.100 000元 B.95 000元
C.90 000元 D.85 000元
解析:由已知得,2020年的就医费用为80 000×10%=8 000(元),故2021年的就医费用为8 000+4 750=12 750(元),所以该教师2021年的家庭总收入为=85 000(元).
答案:D
2.在某中学举行的环保知识竞赛中,将三个年级参赛学生的成绩进行整理后分为5组,绘制如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第二小组的频数是40,则成绩在80~100分的学生人数是( )
A.15 B.18
C.20 D.25
解析:根据频率分布直方图,得第二小组的频率是0.04×10=0.4,因为频数是40,所以样本容量是=100,又成绩在80~100分的频率是(0.01+0.005)×10=0.15,所以成绩在80~100分的学生人数是100×0.15=15.
答案:A
3.在一次53.5千米的自行车个人赛中,25名参赛选手成绩(单位:分钟)的茎叶图如图所示,现将参赛选手按成绩由好到差编为1-25号,再用系统抽样的方法从中选取5人,已知选手甲的成绩为85分钟,若甲被选取,则被选取的其余4名选手的成绩的平均数为( )
A.95 B.96
C.97 D.98
解析:由系统抽样法及已知条件可知被选中的其他4人的成绩分别是88,94,99,107,故平均数为=97.
答案:C
4.在某次赛车中,50名参赛选手的成绩(单位:min)全部介于13到18之间(包括13和18),将比赛成绩分为五组:第一组[13,14),第二组[14,15),…,第五组[17,18].其频率分布直方图如图所示,若成绩在[13,15)内的选手可获奖,则这50名选手中获奖的人数为( )
A.39 B.35
C.15 D.11
解析:由频率分布直方图知成绩在[15,18]内的频率为(0.38+0.32+0.08)×1=0.78,所以成绩在[13,15)内的频率为1-0.78=0.22,则成绩在[13,15)内的选手有50×0.22=11(人),即这50名选手中获奖的人数为11.
答案:D
5.若样本数据x1,x2,…,x10的标准差为8,则数据2x1-1,2x2-1,…,2x10-1的标准差为_________.
解析:依题意,x1,x2,x3,…,x10的方差s2=64,则数据2x1-1,2x2-1,…,2x10-1的方差为22s2=22×64,所以其标准差为=2×8=16.
答案:16
6.在一个容量为5的样本中,数据均为整数,已测出其平均数为10,但墨水污损了两个数据,其中一个数据的十位数字1未被污损,即9,10,11,1■,■,那么这组数据的方差s2可能的最大值是_________.
解析:设这组数据的最后两个分别是10+x,y,则9+10+11+(10+x)+y=50,得x+y=10,故y=10-x,故s2==+x2,显然x取9时,s2有最大值32.8,故答案为32.8.
答案:32.8
7.(2021·合肥调研)第24届冬奥会将于2022年在中国北京和张家口举行.为宣传冬奥会,让更多的人了解、喜爱冰雪项目,某大学举办了冬奥会知识竞赛,并从中随机抽取了100名学生的成绩,绘制成如图所示的频率分布直方图:
(1)试根据频率分布直方图估计,这100人的平均成绩(同一组数据用该组区间的中点值代替);
(2)若采用分层抽样的方法从成绩在[70,80),[80,90),[90,100]的学生中共抽取6人,再将其随机地分配到3个社区开展冬奥会宣传活动(每个社区2人),求“成绩在同一区间的学生分配到不同社区”的概率.
解析:(1)平均成绩=0.02×45+0.16×55+0.22×65+0.30×75+0.20×85+0.10×95=73.00.
(2)由题意知,从成绩在[70,80),[80,90),[90,100]的学生中分别选取了3人,2人,1人.
6人平均分成3组分配到3个社区,共有CC=90种方法.
成绩在同一区间的学生分配到不同社区的方法有AA=36(种),
所以“成绩在同一区间的学生分配到不同社区”的概率P==.
[C组 创新应用练]
某市为了鼓励居民节约用水,拟确定一个合理的月用水量阶梯收费标准,规定一位居民月用水量不超过a吨的部分按平价收费,超出a吨的部分按议价收费.为了解居民的月均用水量(单位:吨),现随机调查1 000位居民,并对收集到的数据进行分组,具体情况见下表:
月均用水量/吨 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3) | [3,3.5) | [3.5,4) | [4,4.5] |
居民数 | 50 | 80 | 5x | 220 | 250 | 80 | 60 | x | 20 |
(1)求x的值,并画出频率分布直方图;
(2)若该市希望使80%的居民月均用水量不超过a吨,试估计a的值,并说明理由;
(3)根据频率分布直方图估计该市居民月用水量的平均值.
解析:(1)由已知得6x=1 000-(50+80+220+250+80+60+20),解得x=40.则月均用水量的频率分布表为
月均用水量/吨 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3) | [3,3.5) | [3.5,4) | [4,4.5] |
频率 | 0.05 | 0.08 | 0.20 | 0.22 | 0.25 | 0.08 | 0.06 | 0.04 | 0.02 |
画出频率分布直方图如图所示.
(2)由(1)知前5组的频率之和为0.05+0.08+0.20+0.22+0.25=0.80,故a=2.5.
(3)由样本估计总体,该市居民月用水量的平均值为0.25×0.05+0.75×0.08+1.25×0.20+1.75×0.22+2.25×0.25+2.75×0.08+3.25×0.06+3.75×0.04+4.25×0.02=1.92.
相关试卷
这是一份高考数学一轮复习第十章第二节随机抽样课时作业理含解析北师大版,共4页。
这是一份高考数学一轮复习第十章第三节用样本估计总体课时作业理含解析北师大版,共7页。
这是一份高考数学一轮复习第十章第二节随机抽样课时作业理含解析北师大版,共4页。












