

所属成套资源:高考数学(理)一轮复习课时规范练含解析新人教版专题
高考数学一轮复习第二章函数导数及其应用第四节幂函数二次函数课时规范练理含解析新人教版
展开这是一份高考数学一轮复习第二章函数导数及其应用第四节幂函数二次函数课时规范练理含解析新人教版,共8页。
第四节 幂函数、二次函数
[A组 基础对点练]
1.已知幂函数f(x)=xα的图象过点(4,2).若f(m)=3,则实数m的值为( )
A. B.±
C.±9 D.9
解析:由f(4)=4α=2可得α=,即f(x)=x,f(m)=m=3,则m=9.
答案:D
2.幂函数y=f(x)的图象过点(4,2),则幂函数y=f(x)的图象是( )
解析:设幂函数的解析式为y=xα,
因为幂函数y=f(x)的图象过点(4,2),
所以2=4α,解得α=.
所以y=,其定义域为[0,+∞),且是增函数,
当0<x<1时,其图象在直线y=x的上方.
答案:C
3.已知幂函数f(x)=xα的图象过点,则函数g(x)=(2x-1)f(x)在区间上的最小值是( )
A.-1 B.0
C.-2 D.
解析:由题设3α=⇒α=-1,故g(x)=(2x-1)x-1=2-在上单调递增,则当x=时取最小值g=2-2=0.
答案:B
4.幂函数y=f(x)的图象经过点(3,),则f(x)是( )
A.偶函数,且在(0,+∞)上是增函数
B.偶函数,且在(0,+∞)上是减函数
C.奇函数,且在(0,+∞)上是增函数
D.非奇非偶函数,且在(0,+∞)上是减函数
解析:设幂函数f(x)=xα,代入点(3,),得=3α,解得α=,所以f(x)=x,可知函数为奇函数,在(0,+∞)上单调递增.
答案:C
5.若a=,b=,c=,则a,b,c的大小关系是( )
A.a<b<c B.c<a<b
C.b<c<a D.b<a<c
解析:因为y=x在第一象限内是增函数,所以a=>b=,因为y=是减函数,所以a=<c=,所以b<a<c.
答案:D
6.若幂函数y=x-1,y=xm与y=xn在第一象限内的图象如图所示,则m与n的取值情况为( )
A.-1<m<0<n<1 B.-1<n<0<m
C.-1<m<0<n D.-1<n<0<m<1
解析:幂函数y=xα,当α>0时,y=xα在(0,+∞)上为增函数,且0<α<1时,图象上凸,∴0<m<1;当α<0时,y=xα在(0,+∞)上为减函数,不妨令x=2,根据图象可得2-1<2n,
∴-1<n<0.
答案:D
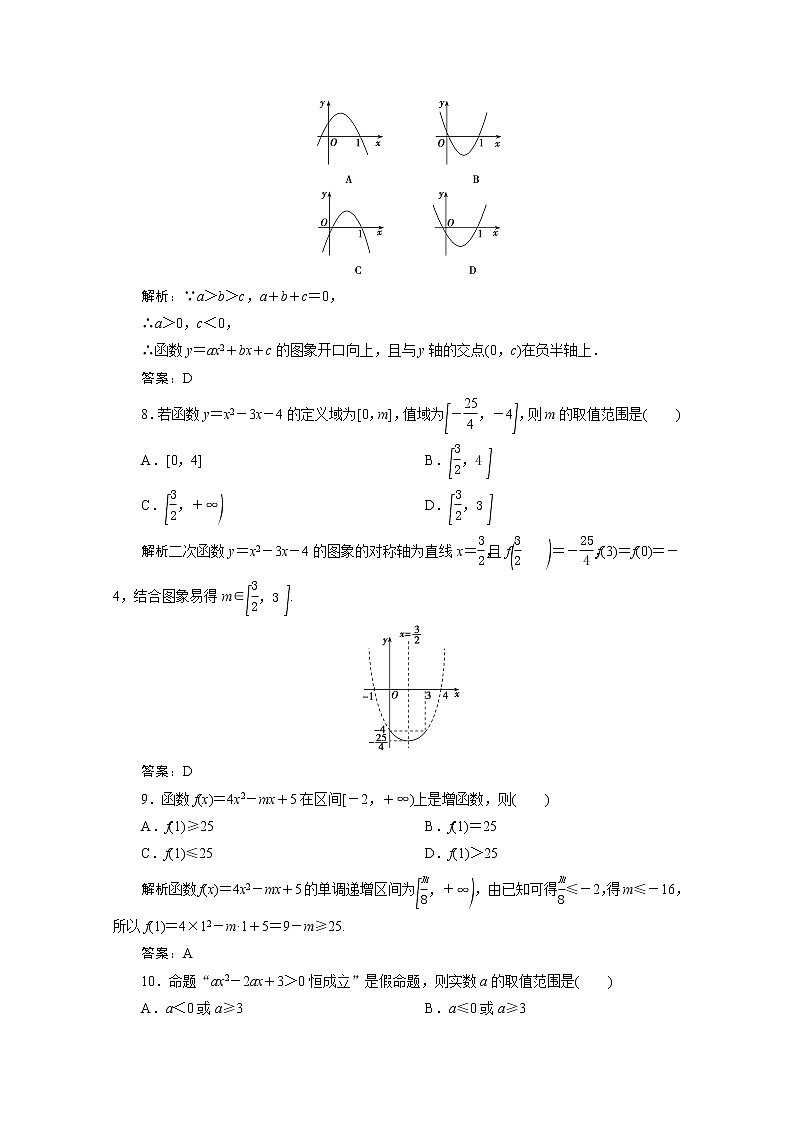
7.已知函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象是( )
解析:∵a>b>c,a+b+c=0,
∴a>0,c<0,
∴函数y=ax2+bx+c的图象开口向上,且与y轴的交点(0,c)在负半轴上.
答案:D
8.若函数y=x2-3x-4的定义域为[0,m],值域为,则m的取值范围是( )
A.[0,4] B.
C. D.
解析:二次函数y=x2-3x-4的图象的对称轴为直线x=,且f=-,f(3)=f(0)=-4,结合图象易得m∈.
答案:D
9.函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,则( )
A.f(1)≥25 B.f(1)=25
C.f(1)≤25 D.f(1)>25
解析:函数f(x)=4x2-mx+5的单调递增区间为,由已知可得≤-2,得m≤-16,所以f(1)=4×12-m·1+5=9-m≥25.
答案:A
10.命题“ax2-2ax+3>0恒成立”是假命题,则实数a的取值范围是( )
A.a<0或a≥3 B.a≤0或a≥3
C.a<0或a>3 D.0<a<3
解析:若ax2-2ax+3>0恒成立,则a=0或可得0≤a<3,故当命题“ax2-2ax+3>0恒成立”是假命题时,a<0或a≥3.
答案:A
11.已知0
12.设二次函数f(x)=ax2-4ax+c在区间[0,2]上单调递减,且f(m)≤f(0),则实数m的取值范围是( )
A.(-∞,0] B.(-∞,0]∪[2,+∞)
C.[2,+∞) D.[0,4]
解析:二次函数f(x)=ax2-4ax+c在区间[0,2]上单调递减,又因为它的对称轴是直线x=2,所以a>0,即函数的图象开口向上,所以f(0)=f(4),则当f(m)≤f(0)时,有0≤m≤4.
答案:D
13.已知α∈.若幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,则α=________.
解析:∵幂函数f(x)=xα为奇函数,∴α可取-1,1,3.又f(x)=xα在(0,+∞)上递减,∴α<0,故α=-1.
答案:-1
14.已知幂函数f(x)= (m∈N*)的图象关于y轴对称,且在(0,+∞)上是减函数,则m的值为________.
解析:因为f(x)在(0,+∞)上是减函数,
所以m2-2m-3<0,解得-1<m<3.
又m∈N*,所以m=1或m=2.
由于f(x)的图象关于y轴对称,
所以m2-2m-3为偶数.
又当m=2时,m2-2m-3为奇数,所以m=2舍去,因此m=1.
答案:1
15.二次函数f(x)的图象经过点(4,3),在x轴上截得的线段长为2,且对∀x∈R,都有f(2+x)=f(2-x),则函数f(x)的解析式为________________.
解析:因为f(2-x)=f(2+x)对x∈R恒成立,
所以f(x)的对称轴为x=2.
又因为f(x)的图象在x轴上截得的线段长为2,
所以f(x)=0的两根为1和3.
设f(x)的解析式为f(x)=a(x-1)(x-3)(a≠0).
又因为f(x)的图象过点(4,3),
所以3a=3,a=1,
所以所求f(x)的解析式为f(x)=(x-1)(x-3),
即f(x)=x2-4x+3.
答案:f(x)=x2-4x+3
16.已知函数f(x)=x2+2x+1,f(x)>x+k在区间[-3,-1]上恒成立,则k的取值范围为________.
解析:由题意得x2+x+1>k在区间[-3,-1]上恒成立.
设g(x)=x2+x+1,x∈[-3,-1],则g(x)在[-3,-1]上递减,
∴g(x)min=g(-1)=1.
∴k<1,故k的取值范围为(-∞,1).
答案:(-∞,1)
[B组 素养提升练]
1.有四个幂函数:①f(x)=x-1;②f(x)=x-2;
③f(x)=x3;④f(x)=x.
某同学研究了其中的一个函数,他给出这个函数的三个性质:(1)偶函数;(2)值域是{y|y∈R,且y≠0};(3)在(-∞,0)上是增函数.如果他给出的三个性质中,有两个正确,一个错误,则他研究的函数是( )
A.① B.②
C.③ D.④
解析:f(x)=x-1只满足(2);f(x)=x3只满足(3);f(x)=x只满足(3).f(x)=x-2是偶函数,在(-∞,0)上是增函数,但是其值域是{y|y>0}.
答案:B
2.已知函数f(x)=ax2+bx+c,且a>b>c,a+b+c=0,集合A={m|f(m)<0},则( )
A.∀m∈A,都有f(m+3)>0
B.∀m∈A,都有f(m+3)<0
C.∃m0∈A,使得f(m0+3)=0
D.∃m0∈A,使得f(m0+3)<0
解析:由a>b>c,a+b+c=0可知a>0,c<0,
且f(1)=0,f(0)=c<0,
即1是方程ax2+bx+c=0的一个根,
当x>1时,f(x)>0.
由a>b,得1>,
设方程ax2+bx+c=0的另一个根为x1,
则x1+1=->-1,即x1>-2,
由f(m)<0可得-2<m<1,
所以1<m+3<4,
由抛物线图象可知f(m+3)>0.
答案:A
3.已知函数f(x)=x2-2tx+1在区间[2,5]上单调且有最大值8,则实数t的值为________.
解析:函数f(x)=x2-2tx+1图象的对称轴是x=t,函数在区间[2,5]上单调,故t≤2或t≥5.
若t≤2,则函数f(x)在区间[2,5]上是增函数,
故f(x)max=f(5)=25-10t+1=8,
解得t=;
若t≥5,函数f(x)在区间[2,5]上是减函数,
此时f(x)max=f(2)=4-4t+1=8,
解得t=-,与t≥5矛盾.
综上所述,t=.
答案:
4.已知函数f(x)=x2-2x,g(x)=ax+2(a>0),对任意的x1∈[-1,2],都存在x0∈[-1,2],使得g(x1)=f(x0),则实数a的取值范围是________.
解析:当x0∈[-1,2]时,由f(x)=x2-2x得f(x0)∈[-1,3],又对任意的x1∈[-1,2],都存在x0∈[-1,2],使得g(x1)=f(x0),所以当x1∈[-1,2]时,g(x1)∈[-1,3].当a>0时,解得a≤.
综上所述,实数a的取值范围是.
答案:
5.(2020·沧州七校联考)已知两函数f(x)=8x2+16x-k,g(x)=2x2+4x+4,其中k为实数.
(1)对任意x∈[-3,3],都有f(x)≤g(x)成立,求k的取值范围;
(2)存在x∈[-3,3],使f(x)≤g(x)成立,求k的取值范围;
(3)对任意x1,x2∈[-3,3],都有f(x1)≤g(x2),求k的取值范围.
解析:(1)设h(x)=f(x)-g(x)=6x2+12x-4-k,问题转化为x∈[-3,3]时,h(x)≤0恒成立,故h(x)max≤0.由二次函数的性质可知h(x)max=h(3)=86-k,有86-k≤0,得k≥86.
(2)由题意,存在x∈[-3,3],使f(x)≤g(x)成立,即h(x)=f(x)-g(x)=6x2+12x-4-k≤0在x∈[-3,3]时有解,故h(x)min≤0.由二次函数的性质可知h(x)min=h(-1)=-10-k,有-10-k≤0,得k≥-10.
(3)对任意x1,x2∈[-3,3],都有f(x1)≤g(x2)成立,所以f(x)max≤g(x)min,x∈[-3,3].由二次函数的性质可得f(x)max=f(3)=120-k,g(x)min=g(-1)=2.故有120-k≤2,得k≥118.
6.已知函数f(x)=bx2-2ax+a(a,b∈R)的图象过点.
(1)当a=2时,求函数f(x)在[0,3]上的最大值和最小值;
(2)若a<0,求使函数f(x)的定义域为[-1,1],值域为[-2,2]的a的值.
解析:(1) ∵函数f(x)=bx2-2ax+a(a,b∈R)的图象过点,∴=b-2a×+a,解得b=1.
当a=2时,f(x)=x2-4x+2,其图象关于x=2对称,
∴f(x)在[0,2]上单调递减,在[2,3]上单调递增,
∴f(x)在[0,3]上的最小值为f(2)=-2,
又f(0)=2,f(3)=-1,∴f(x)在[0,3]上的最大值为f(0)=2.
(2)由(1)知f(x)=x2-2ax+a,
当-1≤a<0时,有
即解得a=-1;
当a<-1时,有
即解得a=-1(舍去).
综上所述,a=-1.
相关试卷
这是一份高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版理,共8页。试卷主要包含了若a<0,则0,5aB等内容,欢迎下载使用。
这是一份广西专用高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版理,共9页。试卷主要包含了若a<0,则0,5aB等内容,欢迎下载使用。
这是一份高考数学一轮复习第二章函数导数及其应用第六节幂函数二次函数课时规范练含解析文北师大版,共5页。试卷主要包含了已知命题p等内容,欢迎下载使用。












