必修 第一册3.3 函数的应用(一)课后复习题

这是一份必修 第一册3.3 函数的应用(一)课后复习题，共10页。
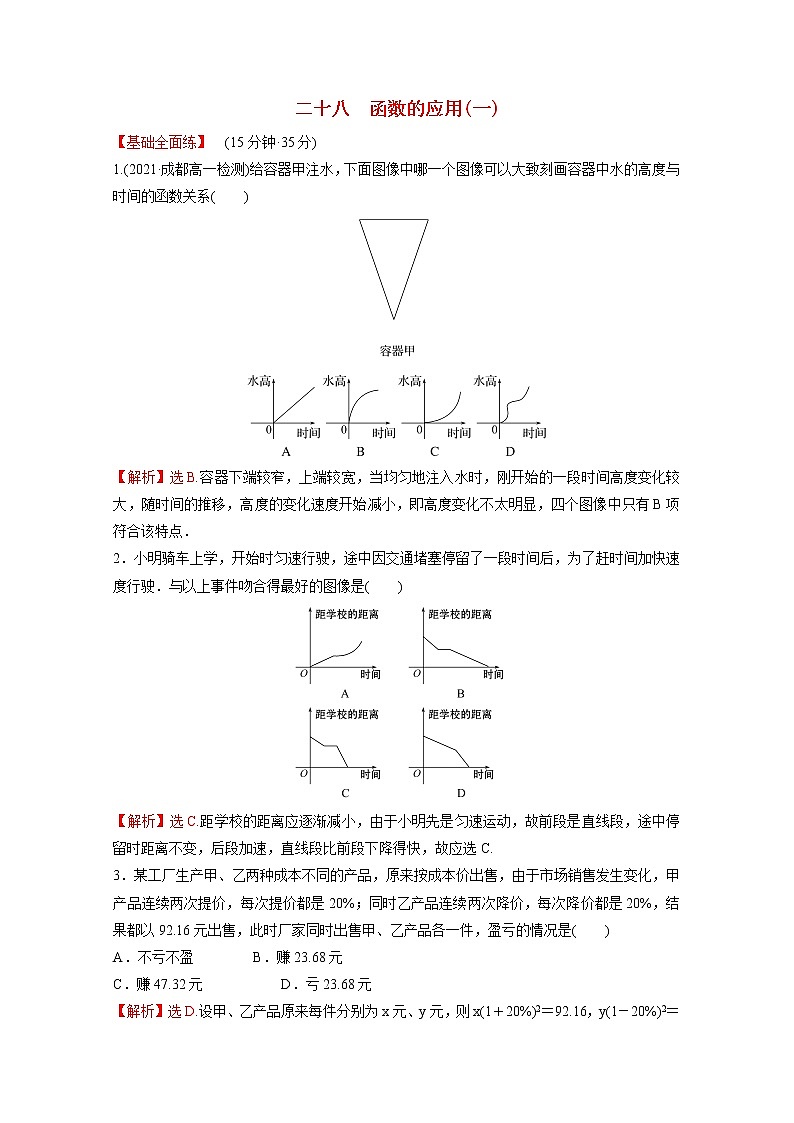
二十八　函数的应用(一)【基础全面练】　(15分钟·35分)1.(2021·成都高一检测)给容器甲注水，下面图像中哪一个图像可以大致刻画容器中水的高度与时间的函数关系(　　)【解析】选B.容器下端较窄，上端较宽，当均匀地注入水时，刚开始的一段时间高度变化较大，随时间的推移，高度的变化速度开始减小，即高度变化不太明显，四个图像中只有B项符合该特点．2．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速度行驶．与以上事件吻合得最好的图像是(　　)【解析】选C.距学校的距离应逐渐减小，由于小明先是匀速运动，故前段是直线段，途中停留时距离不变，后段加速，直线段比前段下降得快，故应选C.3．某工厂生产甲、乙两种成本不同的产品，原来按成本价出售，由于市场销售发生变化，甲产品连续两次提价，每次提价都是20%；同时乙产品连续两次降价，每次降价都是20%，结果都以92.16元出售，此时厂家同时出售甲、乙产品各一件，盈亏的情况是(　　)A．不亏不盈      B．赚23.68元C．赚47.32元      D．亏23.68元【解析】选D.设甲、乙产品原来每件分别为x元、y元，则x(1＋20%)2＝92.16，y(1－20%)2＝92.16，所以x＝64，y＝144，64＋144－92.16×2＝23.68.4．根据统计，一名工人组装第x件产品所用的时间(单位：min)为f(x)＝(a，c为常数).已知工人组装第4件产品用时30 min，组装第a件产品用时5 min，那么c和a的值分别是(　　)A．75，25      B．75，16C．60，144      D．60，16【解析】选C.由题意可得：故应选C.5．某工厂生产某种产品固定成本为2 000万元，并且每生产一单位产品，成本增加10万元．又知总收入K是单位产品数Q的函数，K(Q)＝40Q－Q2，则总利润L(Q)的最大值是________万元．【解析】L(Q)＝40Q－Q2－10Q－2 000＝－Q2＋30Q－2 000＝－(Q－300)2＋2 500，当Q＝300时，L(Q)的最大值为2 500万元．答案：2 500【补偿训练】把总长为16 m的篱笆围成一个矩形场地，则矩形场地的最大面积是________m2.【解析】设一边长为x m，则另一边长可表示为(8－x)m，则面积S＝x(8－x)≤＝16，当且仅当x＝4时取等号，故当矩形的长与宽相等，都为4 m时面积取到最大值16 m2.答案：166．(2021·徐州高一检测)随着科技的发展，智能手机已经开始逐步取代传统PC，渗透进入了人们娱乐生活的各个方面，我们的生活已经步入移动互联网的时代.2020年，某手机企业计划将某项新技术应用到手机生产中去，为了研究市场的反应，计划用一年时间进行试产、试销．通过市场分析，生产此款手机全年需投入固定成本280万，每生产x(千部)手机，需另投入成本C(x)万元，且C(x)＝由市场调研知，每部手机售价0.8万元，且全年内生产的手机当年能全部销售完．(1)求出2020年的利润W(x)(万元)关于年产量x(千部)的函数关系式(利润＝销售额－成本)；(2)2020年产量为多少千部时，企业所获利润最大？最大利润是多少？【解析】(1)当0<x<50时，W(x)＝800x－－280＝－10x2＋600x－280；当x≥50时，W(x)＝800x－－280＝－＋9 170，所以W(x)＝(2)若0<x<50，W(x)＝－10(x－30)2＋8 720，当x＝30时，W(x)max＝8 720万元；若x≥50，W(x)＝－＋9 170≤－2＋9 170＝8 970，当且仅当x＝时，即x＝100时，W(x)max＝8 970万元．因为8 970>8 720，所以2020年产量为100千部时，企业所获利润最大，最大利润是8 970万元．【综合突破练】　　(30分钟·60分)一、单选题(每小题5分，共20分)1．某工厂2017年的产量为A，2018年的增长率为a，2019年的增长率为b，这两年的平均增长率为x，则有(　　)A．x＝(a＋b)       B．x≤(a＋b)C．x>(a＋b)      D．x≥(a＋b)【解析】选B.由(1＋x)2＝(1＋a)(1＋b)≤，所以x≤(a＋b).2．某店从水果批发市场购得椰子两筐，连同运费总共花了300元，回来后发现有12个是坏的，不能将它们出售，余下的椰子按高出成本价1元/个售出，售完后共赚78元．则这两筐椰子原来的总个数为(　　)A．180    B．160    C．140    D．120【解析】选D.设原来两筐椰子的总个数为x，成本价为a元/个，则解得故这两筐椰子原来共有120个．3．(2021·武汉高一检测)疫情暴发期间某种防护用品在近30天内每件的销售价格P(元)和时间t(天)的函数关系为：P＝，设该商品的日销售量Q(件)与时间t(天)的函数关系为Q＝40－t，则这种商品的日销售金额最大时是第____天．(　　)A．10    B．20    C．25    D．30【解析】选C.由题意得：y＝.当0＜t＜25，t∈N*时，y＝(t＋20)(40－t)＝－t2＋20t＋800＝－(t－10)2＋900.所以t＝10天时，ymax＝900元，当25≤t≤30，t∈N*时，y＝(－t＋100)(40－t)＝t2－140t＋4 000＝(t－70)2－900，而y＝(t－70)2－900，在t∈[25，30]时，函数递减，所以t＝25天时，ymax＝1 125元．因为1 125＞900，所以第25天日销售额最大为1 125元．4．(2021·福州高一检测)用一段长为36米的篱笆围成一个一边靠墙的矩形菜园．已知墙长20米，则菜园面积的最大值是(　　)A．144    B．160    C．162    D．180【解析】选C.设菜园靠墙一边的长为x米，则矩形菜园的宽为米，且0<x≤20，则菜园面积y＝x·＝·x·≤×2＝162.当且仅当x＝36－x，即x＝18时等号成立．二、多选题(每小题5分，共10分，全部选对得5分，选对但不全的得3分，有选错的得0分)5．如图是本地区一种产品30天的销售图像，图①是产品日销售量y(单位：件)与时间t(单位：天)之间的函数关系，图②是一件产品的销售利润z(单位：元)与时间t(单位：天)之间的函数关系，已知日销售利润＝日销售量×一件产品的销售利润，下列结论正确的是(　　)A．第24天的销售量为200件B．第10天销售一件产品的利润是15元C．第12天与第30天这两天的日销售利润相等D．第30天的日销售利润是750元【解析】选ABD.对于A选项，在图①中，t＝24时，y＝200，故A选项结论正确．对于B选项，根据图②，，的中点坐标为，故B选项结论正确．对于D选项，由图①知第30天销售150件，由图②知第30天一件产品利润为5元，故日销售利润为150×5＝750元，故D选项结论正确．由①知(0，100)，(24，200)的中点为(12，150)，即第12天和第30天的销售量相同，根据图②，第12天的一件产品利润高于第30天一件产品利润，故第12天与第30天这两天的日销售利润不相等，故C选项结论错误．故选ABD.6．一个人以6m/s的速度去追停在交通灯前的汽车，当他离汽车25 m时，交通灯由红变绿，汽车以1m/s2的加速度匀加速开走，那么下列选项不正确的是(　　)A．人可在7 s内追上汽车B．人可在10 s内追上汽车C．人追不上汽车，其间距最少为5 mD．人追不上汽车，其间距最少为7 m【解析】选ABC.设汽车经过t s行驶的路程为s m，则s＝t2，车与人的间距d＝(s＋25)－6t＝t2－6t＋25＝2＋7，当t＝6时，d取得最小值7，D项正确．故选ABC.【补偿训练】某沙漠地区的某时段气温与时间的函数关系式是f＝－t2＋24t－101，则该沙漠地区在该时段的最高气温与最低气温分别是(　　)A．43    B．－21    C．21    D．58 【解析】选AB.f＝－t2＋24t－101的对称轴为t＝12，所以f在上递增，在上递减；所以fmax＝f＝43 , fmin＝f＝－21.三、填空题(每小题5分，共10分)7．甲同学家到乙同学家的途中有一公园，甲同学家到公园的距离与乙同学家到公园的距离都是2 km.如图表示甲从家出发到乙同学家经过的路程y(km)与时间x(min)的关系，其中甲在公园休息的时间是10 min，那么y＝f(x)的解析式为________.【解析】由题图知所求函数是一个分段函数，且各段均是直线，可用待定系数法求得y＝f(x)＝答案：y＝f(x)＝8．长为4、宽为3的矩形，当长增加x，且宽减少时面积最大，此时x＝____，最大面积S＝______．【解析】S＝(4＋x)＝－＋x＋12＝－(x－1)2，当x＝1时，Smax＝.答案：1　四、解答题(每小题10分，共20分)9．(2021·太原高一检测)某企业加工生产一批珠宝，要求每件珠宝都按统一规格加工，每件珠宝的原材料成本为0.5万元，每件珠宝售价(万元)与加工时间t(单位：天)之间的关系满足图1，珠宝的预计销量(件)与加工时间t(天)之间的关系满足图2.原则上，单件珠宝的加工时间不能超过55天，企业支付的工人报酬为这批珠宝销售毛利润的三分之一，其他成本忽略不计算．(1)如果每件珠宝加工天数分别为5，13，预计销量分别会有多少件？(2)设工厂生产这批珠宝产生的纯利润为S(万元)，请写出纯利润S(万元)关于加工时间t(天)之间的函数关系式，并求纯利润S(万元)最大时的预计销量．注：毛利润＝总销售额 — 原材料成本，纯利润＝毛利润 — 工人报酬．【解析】(1)预计订单函数f(t)(t∈N)为f(t)＝，f(5)＝20＋5＝25，f(13)＝－13＋55＝42，所以每件珠宝加工天数分别为5，13，预计销量分别为25件，42件．(2)售价函数为g(t)＝1.5t＋5，所以利润函数为S(t)＝S(t)＝＝当0≤t≤10时，S(t)＝4t2＋17t＋15的最大值为S(10)＝585; 当10<t≤55时，S(t)＝－(t2－52t－165)的最大值为S(26)＝841>585，故利润最大时，t＝26，此时预计的销量为26件．10．已知某企业原有员工2 000人，每人每年可为企业创利3.5万元．为应对新型冠状病毒肺炎疫情给企业带来的不利影响，该企业实施“优化重组，分流增效”的策略，分流出一部分员工待岗．为维护生产稳定，该企业决定待岗人数不超过原有员工的5%，并且每年给每位待岗员工发放生活补贴0.5万元．据评估，当待岗员工人数x不超过原有员工1 %时，留岗员工每人每年可为企业多创利万元；当待岗员工人数x超过原有员工1%时，留岗员工每人每年可为企业多创利0.9万元．为使企业年利润最大，应安排多少员工待岗？【解析】设重组后，该企业年利润为y万元．当待岗人员不超过1%时，由1－＞0，x≤2 000×1%＝20，得<x≤20(x∈N)，则y＝(2 000－x)－0.5x＝－5＋9 000.64；当待岗人员超过1%且不超过5%时，由20<x≤2 000×5%，得20<x≤100(x∈N)，则y＝(2 000－x)(3.5＋0.9)－0.5x＝－4.9x＋8 800.故y＝当<x≤20且x∈N时，有x＋≥2＝32，则y＝－5＋9 000.64≤－5×32＋9 000.64＝8 840.64，当且仅当x＝，即x＝16时取等号，此时y取得最大值8 840.64；当20<x≤100且x∈N时，函数y＝－4.9x＋8 800为减函数．所以y<－4.9×20＋8 800＝8 702.又8 840.64＞8 702，故当x＝16时，y有最大值8 840.64.即要使企业年利润最大，应安排16名员工待岗．【应用创新练】　　某特许专营店销售福州市成功举办第一届全国青年运动会的纪念章，每枚进价5元，同时每销售一枚这种纪念章还需向组委会交特许经营管理费2元，预计这种纪念章以每枚20元的价格销售时该店一个月内可销售2 000枚，经过市场调研发现每枚纪念章的价格在20元的基础上每减少一元则增加销售400枚，而每增加一元则减少销售100枚．现设每枚纪念章的销售价格为x(x∈N)元．(1)写出该特许专营店一个月内销售这种纪念章所获得的利润y(元)与每枚纪念章的销售价格x(元)的函数关系式，并写出这个函数的定义域．(2)当每枚纪念章的销售价格x为多少元时，该特许专营店一个月内利润y(元)最大？并求利润的最大值．【解析】(1)由题意可得：y＝(x∈N)且由题意有：x－7≥0，所以x≥7，同时，2 000－100(x－20)≥0，所以x≤40.所以，函数的定义域为：{x}．(2)由(1)有：y＝(x∈N)，①当7≤x＜20(x∈N)时，y＝(x－7)＝－400(x－16)2＋32 400，所以当x＝16时，在此段有最大利润32 400元. ②又当20≤x≤40(x∈N)时，y＝(x－7)[2 000－100(x－20)]＝－1002＋27 225.所以当x＝23或x＝24时，在此段有最大利润27 200元. 综合①②可知，当x＝16时，该特许专营店一个月内利润最大，这个最大值为32 400.【补偿训练】某企业生产A，B两种产品，根据市场调查与预测，A产品的利润与投资成正比，其关系如图①；B产品的利润与投资的算术平方根成正比，其关系如图②.(注：利润和投资单位：万元)(1)分别将A，B两种产品的利润表示为投资的函数关系式；(2)已知该企业已筹集到18万元资金，并将全部投入A，B两种产品的生产，怎样分配这18万元投资，才能使该企业获得最大利润？其最大利润约为多少万元？【解析】(1)根据题意可设A，B产品的利润与投资的函数关系式为f＝k1x, g＝k2.则f(x)＝0.25x(x≥0)，g(x)＝2(x≥0).(2)设B产品投入x万元，A产品投入(18－x)万元，该企业可获总利润为y万元．则y＝(18－x)＋2，0≤x≤18，令＝t，t∈[0，3]，则y＝(－t2＋8t＋18)＝－(t－4)2＋.所以当t＝4时，ymax＝＝8.5, 此时x＝16，18－x＝2.所以当A，B两种产品分别投入2万元、16万元时，可使该企业获得最大利润，约为8.5万元．