这是一份数学必修第四册11.1.5 旋转体课时训练，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．下列几何体中是旋转体的是( )
①圆柱；②六棱锥；③正方体；④球体；⑤四面体．
A．①和⑤ B．①
C．③和④D．①和④
2．下面几何体的轴截面(过旋转轴的截面)是圆面的是( )
A．圆柱B．圆锥
C．球D．圆台
3．以钝角三角形的较小边所在的直线为轴，其他两边旋转一周所得到的几何体是( )
A．两个圆锥拼接而成的组合体
B．一个圆台
C．一个圆锥
D．一个圆锥挖去一个同底的小圆锥
4．用一个平面去截一个几何体，得到的截面是圆面，这个几何体不可能是( )
A．圆锥B．圆柱
C．球D．棱柱
二、填空题
5．如图是一个几何体的表面展开图形，则这个几何体是________．
6．直角梯形绕其较长底边所在直线旋转一周，所得旋转体的结构特征是________．
7．一个圆锥的母线长为20cm，母线与轴的夹角为30°，则圆锥的高为________cm.
三、解答题
8．指出如图①②所示的图形是由哪些简单几何体构成的．
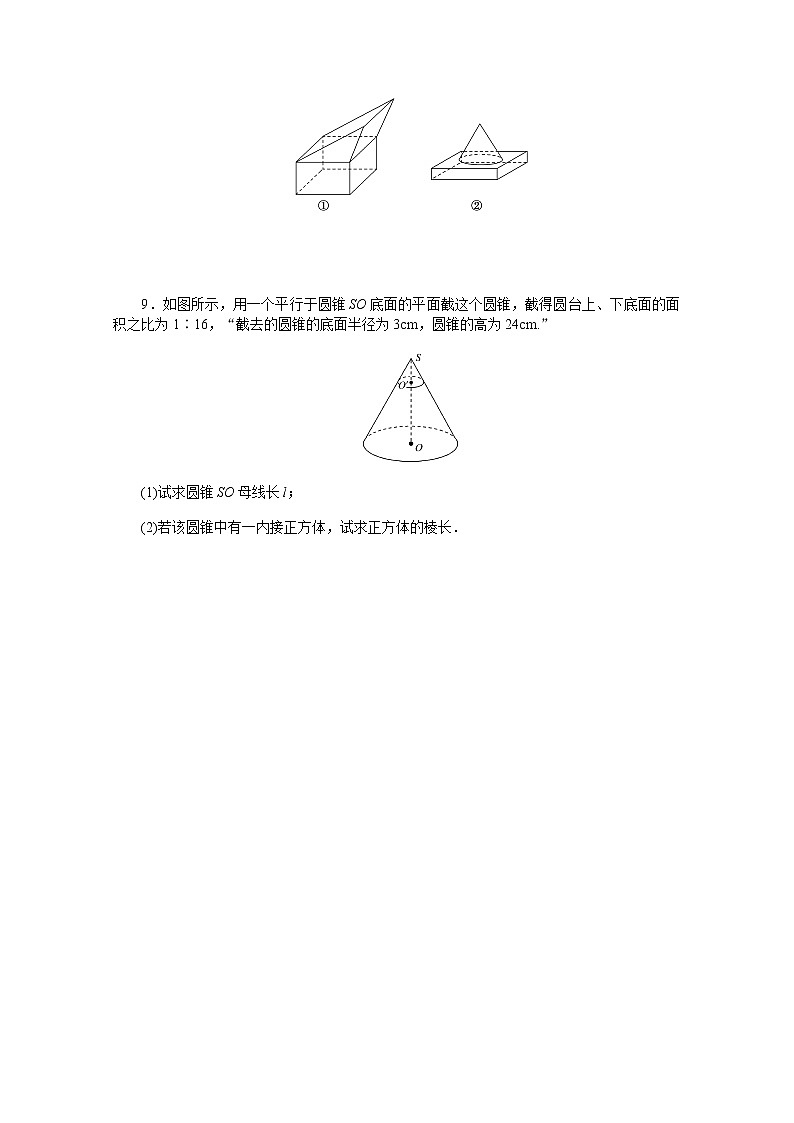
9．如图所示，用一个平行于圆锥SO底面的平面截这个圆锥，截得圆台上、下底面的面积之比为1∶16，“截去的圆锥的底面半径为3cm，圆锥的高为24cm.”
(1)试求圆锥SO母线长l；
(2)若该圆锥中有一内接正方体，试求正方体的棱长．
[尖子生题库]
10．在如图所示的斜截圆柱中，已知圆柱底面的直径为40cm，母线长最短50cm、最长80cm，则斜截圆柱侧面面积S＝________cm2.
课时作业(十二) 旋转体
1．解析：根据旋转体的概念可知，①和④是旋转体．
答案：D
2．解析：圆柱的轴截面是矩形，圆锥的轴截面是等腰三角形，圆台的轴截面是等腰梯形，只有球的轴截面是圆面．
答案：C
3．解析：如图，以AB为轴旋转所得的几何体是一个大圆锥挖去一个同底的小圆锥．
答案：D
4．解析：用一个平面去截圆锥、圆柱、球均可以得到圆面，但截棱柱一定不会产生圆面．
答案：D
5．解析：一个长方形和两个圆折叠后，能围成的几何体是圆柱．
答案：圆柱
6．解析：由旋转体的定义知，该几何体为一个圆锥和一个圆柱拼接成的组合体．
答案：一个圆锥和一个圆柱拼接成的组合体
7．解析：如图是圆锥的轴截面，
则SA＝20cm，∠ASO＝30°，
∴AO＝10cm，SO＝10eq \r(3)cm.
答案：10eq \r(3)
8．解：图①是由一个三棱柱和一个四棱柱拼接而成的简单组合体．
图②是由一个圆锥和一个四棱柱拼接而成的简单组合体．
9．解：(1)由截得圆台上、下底面面积之比为1∶16，可设截得圆台的上、下底面的半径分别为r,4r.
过轴SO作截面，如图所示．
则△SO′A′∽△SOA，O′A′＝3，
∴eq \f(O′A′,OA)＝eq \f(1,4)，
∴OA＝12cm.
又SO＝24cm，
∴SA＝eq \r(122＋242)＝12eq \r(5)cm.
即圆锥SO的母线长为12eq \r(5)cm.
(2)如图，过正方体的体对角线作圆锥的轴截面，设正方体的棱长为x，则
OC＝eq \f(\r(2),2)x，
∴eq \f(\f(\r(2),2)x,12)＝eq \f(24－x,24)，
解得x＝24(eq \r(2)－1)，
∴正方体的棱长为24(eq \r(2)－1) cm.
10．解析：将侧面展开可得S＝eq \f(1,2)(50＋80)×40π＝2600π(cm2)．
答案：2600π

相关试卷更多