人教B版 (2019)必修 第一册3.1.1 函数及其表示方法第2课时达标测试

课后素养落实(二十)　函数的表示方法

(建议用时：40分钟)

一、选择题

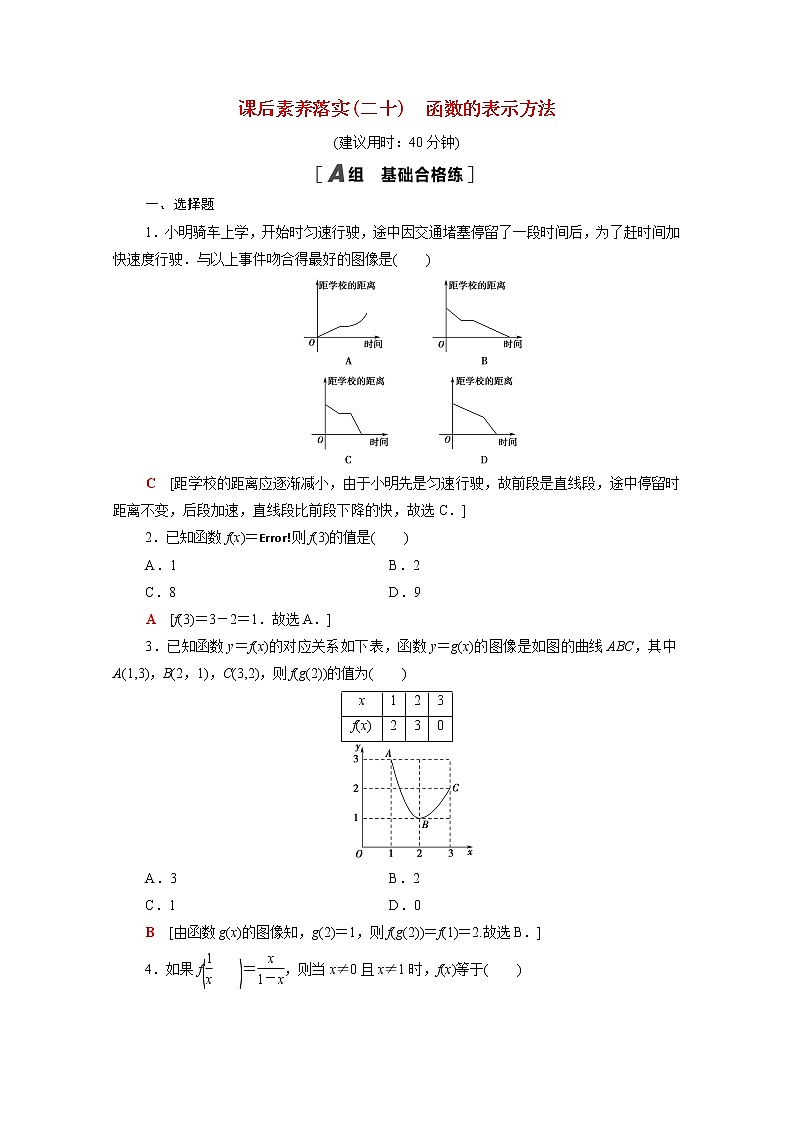
1．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速度行驶．与以上事件吻合得最好的图像是(　　)

C　[距学校的距离应逐渐减小，由于小明先是匀速行驶，故前段是直线段，途中停留时距离不变，后段加速，直线段比前段下降的快，故选C．]

2．已知函数f(x)＝则f(3)的值是(　　)

A．1　　 B．2　　　　　

C．8　　　　　 D．9

A　[f(3)＝3－2＝1．故选A．]

3．已知函数y＝f(x)的对应关系如下表，函数y＝g(x)的图像是如图的曲线ABC，其中A(1,3)，B(2，1)，C(3,2)，则f(g(2))的值为(　　)

A．3 B．2

C．1 D．0

B　[由函数g(x)的图像知，g(2)＝1，则f(g(2))＝f(1)＝2.故选B．]

4．如果f＝，则当x≠0且x≠1时，f(x)等于(　　)

A． B．

C． D．－1

B　[令＝t，则x＝，代入f＝，则有f(t)＝＝，所以f(x)＝(x≠0，且x≠1)，故选B．]

5．(多选题)设函数f(x)＝若f(a)＋f(－1)＝2，则a可以取的值为(　　)

A．－3 B．3

C．－1 D．1

CD　[因为f(－1)＝＝1，所以f(a)＝1．

(1)当a≥0时，f(a)＝＝1，所以a＝1．

(2)当a<0时，f(a)＝＝1，所以a＝－1．

综上可知a＝1或－1．]

二、填空题

6．设函数f(x)＝，若f(m)＞m，则实数m的取值范围是________．

(－∞，－1)　[由题意，得或，解得m＜－1．]

7．已知函数f(x)的图像如图所示，则f(x)的解析式是________．

f(x)＝　[由题图可知，图像是由两条线段组成，

当－1≤x<0时，设f(x)＝ax＋b，将(－1,0)，(0,1)代入解析式，得∴即f(x)＝x＋1．

当0≤x≤1时，设f(x)＝kx，将(1，－1)代入，则k＝－1，即f(x)＝－x.

综上，f(x)＝]

8．若一个长方体的高为80 cm，长比宽多10 cm，则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________．

y＝80x(x＋10)，x∈(0，＋∞)　[由题意可知，长方体的长为(x＋10)cm，从而长方体的体积y＝80x(x＋10)，x>0.]

三、解答题

9．(1)已知f(x)是一次函数，且满足2f(x＋3)－f(x－2)＝2x＋21，求f(x)的解析式；

(2)已知f(x)为二次函数，且满足f(0)＝1，f(x－1)－f(x)＝4x，求f(x)的解析式；

(3)已知f＝x2＋＋1，求f(x)的解析式．

[解]　(1)设f(x)＝ax＋b(a≠0)，

则2f(x＋3)－f(x－2)＝2[a(x＋3)＋b]－[a(x－2)＋b]＝2ax＋6a＋2b－ax＋2a－b＝ax＋8a＋b＝2x＋21，

所以a＝2，b＝5，所以f(x)＝2x＋5.

(2)因为f(x)为二次函数，设f(x)＝ax2＋bx＋c(a≠0)．

由f(0)＝1，得c＝1．

又因为f(x－1)－f(x)＝4x，

所以a(x－1)2＋b(x－1)＋c－(ax2＋bx＋c)＝4x，整理，得－2ax＋a－b＝4x，求得a＝－2，b＝－2，

所以f(x)＝－2x2－2x＋1．

(3)∵f＝＋2＋1＝2＋3.∴f(x)＝x2＋3(x≠0)．

10．已知函数f(x)＝

(1)求f(－1)，f，f(4)的值；

(2)求函数的定义域、值域．

[解]　(1)易知f(－1)＝0，f＝－×＝－，f(4)＝3.

(2)作出图像如图所示．利用数形结合易知f(x)的定义域为[－1，＋∞)，值域为(－1,2]∪{3}．

1．若函数y＝x2－3x－4的定义域为[0，m]，值域为，则m的取值范围是(　　)

A．(0,4]　　　　　　 B．

C． D．

C　[因为y＝x2－3x－4＝2－，所以对称轴为直线x＝，当x＝时，y＝－.

因为x＝0时，y＝－4，由二次函数图像可知

解得≤m≤3，所以m的取值范围是.]

2．(多选题)已知f(x)＝则满足不等式xf(x)＋x≤2的x的值有(　　)

A．1 B．2

C．3 D．－1

AD　[当x≥0时，f(x)＝1，代入xf(x)＋x≤2，解得x≤1，所以0≤x≤1；

当x<0时，f(x)＝0，代入xf(x)＋x≤2，

解得x≤2，所以x<0.综上可知x≤1．结合选项得AD符合条件．]

3．在平面直角坐标系xOy中，若直线y＝2a与函数y＝|x－a|－1的图像只有一个交点，则a的值为________．

－　[在同一平面直角坐标系内，作出直线y＝2a与函数y＝|x－a|－1的大致图像，如图所示．

由题意，可知2a＝－1，则a＝－.]

4．已知f(x)＝

(1)若f(x)≥，则x的取值范围为________；

(2)f(x)的值域为________．

(1)∪　(2)[0,1]　[(1)利用描点法，作出f(x)的图像，如图所示．由于f＝，结合此函数图像可知，使f(x)≥的x的取值范围是∪.

(2)由图像知，当－1≤x≤1时，

f(x)＝x2的值域为[0,1]，

当x>1或x<－1时，f(x)＝1．

所以f(x)的值域为[0,1]．]

设函数f(x)＝

(1)请在下列直角坐标系中画出函数f(x)的图像；

(2)根据(1)的图像，试分别写出函数f(x)与函数y＝t的图像有2,3,4个交点时，相应的实数t的取值范围；

(3)记函数g(x)的定义域为D，若存在x0∈D，使g(x0)＝x0成立，则称点(x0，x0)为函数g(x)图像上的不动点．试问，函数f(x)图像上是否存在不动点，若存在，求出不动点的坐标；若不存在，请说明理由．

[解]　(1)函数f(x)的图像如图：

(2)根据图像可知当－2<t<1或t>2时，

f(x)与y＝t有2个交点；

当t＝1或t＝2时，f(x)与y＝t有3个交点；

当1<t<2时，f(x)与y＝t有4个交点．

(3)若f(x)图像上存在不动点，

则f(x)＝x有解，则y＝f(x)与y＝x有交点．

由图像可知：

若－1≤x≤2，则－x2＋2＝x，

解得x＝1(舍去x＝－2)，即不动点为(1,1)；

若x>2，则3x－8＝x，

解得x＝4，即不动点为(4,4)．

综上，函数f(x)图像上存在不动点(1,1)，(4,4).