人教A版 (2019)选择性必修第一册第一章空间向量与立体几何本章综合与测试习题

展开

这是一份人教A版 (2019)选择性必修第一册第一章空间向量与立体几何本章综合与测试习题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

章末综合测评(一)　空间向量与立体几何
(满分：150分　时间：120分钟)
一、选择题(本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)
1．已知a＝(－3,2,5)，b＝(1,5，－1)，则a·(a＋3b)＝(　　)
A．(0,34,10) B．(－3,19,7)
C．44 D．23
C　[a＋3b＝(－3,2,5)＋3(1,5，－1)＝(0,17,2)，则a·(a＋3b)＝(－3,2,5)·(0,17,2)＝0＋34＋10＝44.]
2．设l1的方向向量为a＝(1,2，－2)，l2的方向向量为b＝(－2,3，m)，若l1⊥l2，则m等于(　　)
A．1 B．2
C． D．3
B　[若l1⊥l2，则a⊥b，∴a·b＝0，
∴1×(－2)＋2×3＋(－2m)＝0，解得m＝2.]
3．在空间四边形ABCD中，若向量＝(－3,5,2)，＝(－7，－1，－4)，点E，F分别为线段BC，AD的中点，则的坐标为(　　)
A．(2,3,3) B．(－2，－3，－3)
C．(5，－2,1) D．(－5,2，－1)
B　[取AC中点M，连接ME，MF(图略)，
则＝＝，＝＝，
所以＝－＝(－2，－3，－3)，故选B．]
4．如图所示，在平行六面体ABCDA1B1C1D1中，点E为上底面对角线A1C1的中点，若＝＋x＋y，则(　　)

A．x＝－，y＝
B．x＝，y＝－
C．x＝－，y＝－
D．x＝，y＝
A　[＝＋＋＝－＋＋(＋)＝－＋＋＋＝－＋＋，∴x＝－，y＝.]
5．已知A(2，－5,1)，B(2，－4,2)，C(1，－4,1)，则与的夹角为(　　)
A．30° B．60°
C．45° D．90°
B　[由题意得＝(0,1,1)，＝(－1,1,0)，cos〈，〉＝＝＝，所以与的夹角为60°.]
6．已知二面角αlβ的大小为，m，n为异面直线，且m⊥α，n⊥β，则m，n所成的角为(　　)
A． B．
C． D．
B　[设m，n的方向向量分别为m，n.由m⊥α，n⊥β知m，n分别是平面α，β的法向量．∵|cos〈m，n〉|＝cos ＝，∴〈m，n〉＝或.但由于两异面直线所成的角的范围为，故异面直线m，n所成的角为.]
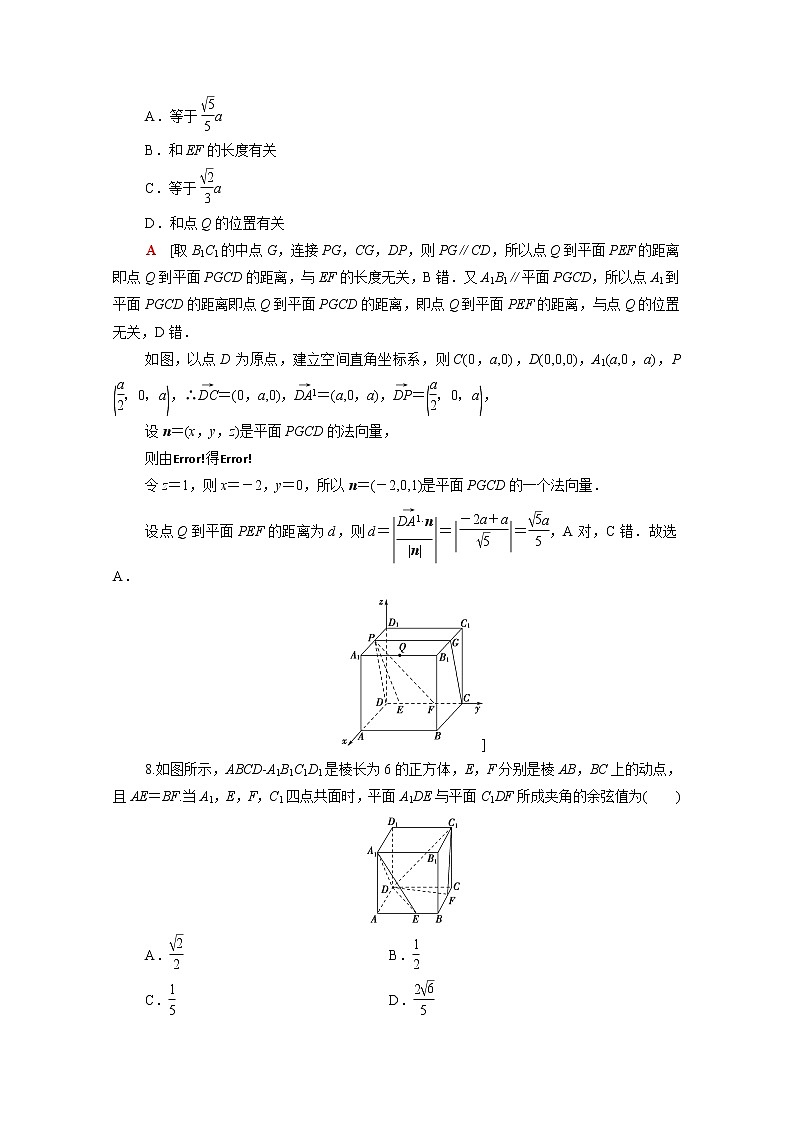
7.如图，在棱长为a的正方体ABCDA1B1C1D1中，P为A1D1的中点，Q为A1B1上任意一点，E，F为CD上两个动点，且EF的长为定值，则点Q到平面PEF的距离(　　)

A．等于a
B．和EF的长度有关
C．等于a
D．和点Q的位置有关
A　[取B1C1的中点G，连接PG，CG，DP，则PG∥CD，所以点Q到平面PEF的距离即点Q到平面PGCD的距离，与EF的长度无关，B错．又A1B1∥平面PGCD，所以点A1到平面PGCD的距离即点Q到平面PGCD的距离，即点Q到平面PEF的距离，与点Q的位置无关，D错．
如图，以点D为原点，建立空间直角坐标系，则C(0，a,0)，D(0,0,0)，A1(a,0，a)，P，∴＝(0，a,0)，＝(a,0，a)，＝，
设n＝(x，y，z)是平面PGCD的法向量，
则由得
令z＝1，则x＝－2，y＝0，所以n＝(－2,0,1)是平面PGCD的一个法向量．
设点Q到平面PEF的距离为d，则d＝＝＝，A对，C错．故选A．
]
8.如图所示，ABCDA1B1C1D1是棱长为6的正方体，E，F分别是棱AB，BC上的动点，且AE＝BF.当A1，E，F，C1四点共面时，平面A1DE与平面C1DF所成夹角的余弦值为(　　)

A． B．
C． D．
B　[以D为原点，DA、DC、DD1所在直线分别为x轴，y轴，z轴建立空间直角坐标系，易知当E(6,3,0)，F(3,6,0)时，A1，E，F，C1共面，设平面A1DE的法向量为n1＝(a，b，c)，依题意得

可取n1＝(－1,2,1)，同理可得平面C1DF的一个法向量为n2＝(2，－1,1)，
故平面A1DE与平面C1DF的夹角的余弦值为＝.故选B．]
二、选择题(本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得3分)
9．已知正方体ABCD A1B1C1D1的中心为O，则下列结论中正确的有(　　)
A．＋与＋是一对相反向量
B．－与－是一对相反向量
C．＋＋＋与＋＋＋是一对相反向量
D．－与－是一对相反向量
ACD　[∵O为正方体的中心，∴＝－，＝－，故＋＝－(＋)，同理可得＋＝－(＋)，故＋＋＋＝－(＋＋＋)，∴AC正确；∵－＝，－＝，∴－与－是两个相等的向量，∴B不正确；∵－＝，－＝＝－，∴－＝－(－)，∴D正确．]
10．在以下选项中，不正确的命题有(　　)
A．|a|－|b|＝|a＋b|是a，b共线的充要条件
B．若a∥b，则存在唯一的实数λ，使a＝λb
C．对空间任意一点O和不共线的三点A，B，C，若＝2－2－，则P，A，B，C四点共面
D．若{a，b，c}为空间的一个基底，则{a＋b，b＋c，c＋a}构成空间的另一个基底
ABC　[A．|a|－|b|＝|a＋b|⇒a与b共线，但a与b共线时|a|－|b|＝|a＋b|不一定成立，故不正确；B．b需为非零向量，故不正确；C．因为2－2－1≠1，由共面向量定理知，不正确；D．由基底的定义知正确．]
11．下列说法正确的是(　　)
A．直线l的方向向量a＝(1，－1,2)，直线m的方向向量b＝，则l与m垂直
B．直线l的方向向量a＝(0,1，－1)，平面α的法向量n＝(1，－1，－1)，则l⊥α
C．平面α，β的法向量分别为n1＝(0,1,3)，n2＝(1,0,2)，则α∥β
D．平面α经过三点A(1,0，－1)，B(0,1,0)，C(－1,2,0)，向量n＝(1，u，t)是平面α的法向量，则u＋t＝1
AD　[对于A，∵a＝(1，－1,2)，b＝，∴a·b＝1×2＋(－1)×1＋2×＝0，∴a⊥b，∴直线l与m垂直，A正确．
对于B，∵a＝(0,1，－1)，n＝(1，－1，－1)，∴a·n＝0×1＋1×(－1)＋(－1)×(－1)＝0，∴a⊥n，∴l∥α或l⊂α，B错误．
对于C，∵n1＝(0,1,3)，n2＝(1,0,2)，∴n1与n2不共线，∴α∥β不成立，C错误．
对于D，由于A(1,0，－1)，B(0,1,0)，C(－1,2,0)，则＝(－1,1,1)，＝(－1,1,0)，
又向量n＝(1，u，t)是平面α的法向量，∴即则u＋t＝1，D正确．]
12．如图(1)是一副直角三角板的示意图．现将两三角板拼成直二面角，得到四面体ABCD，如图(2)所示，则下列结论中正确的是(　　)

A．·＝0
B．平面BCD的法向量与平面ACD的法向量垂直
C．异面直线BC与AD所成的角为60°
D．直线DC与平面ABC所成的角为30°
AD　[以B为坐标原点，分别以，的方向为x轴，y轴的正方向建立空间直角坐标系，如图所示．设BD＝2，则B(0,0,0)，D(2,0,0)，C(0,2，0)，A(0，，)，∴＝(2,0,0)，＝(0，，－)，＝(0,2，0)，＝(2，－，－)，＝(－2,2，0)．
∴·＝(2,0,0)·(0，，－)＝0，A正确；易得平面BCD的一个法向量为n1＝(0,0，)，平面ACD的一个法向量为n2＝(，1,1)，n1·n2≠0，B错误；
|cos〈，〉|＝＝＝≠，C错误；易得平面ABC的一个法向量为＝(2,0,0)，设直线DC与平面ABC所成的角为θ，则sin θ＝＝＝，故D正确．]
三、填空题(本题共4小题，每小题5分，共20分．把答案填在题中的横线上)
13．已知＝(1,5，－2)，＝(3,1，z)，若⊥BC，＝(x－1，y，－3)，且⊥平面ABC，则＝________.
　[∵⊥，∴·＝0，∴3＋5－2z＝0，∴z＝4.
∵＝(x－1，y，－3)，且⊥平面ABC，
∴即
解得
故＝.]
14．已知a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，若a，b，c共面，则λ＝________.
　[易知a与b不共线，由共面向量定理可知，要使a，b，c共面，则必存在实数x，y，使得c＝xa＋yb，即解得]
15．已知A(0,0，－x)，B(1，，2)，C(x，，2)三点，点M在平面ABC内，O是平面ABC外一点，且＝x＋2x＋4，则x＝________，与的夹角为________．(本题第一空2分，第二空3分)
－1　　[由A，B，C，M四点共面可知x＋2x＋4＝1，∴x＝－1.
∴A(0,0,1)，C(－1，，2)，∴＝(1，，1)，＝(－1，，1)，
∴cos〈，〉＝＝，即与的夹角为.]
16．如图，等边三角形ABC与正方形ABDE有一公共边AB，二面角CABD的余弦值为，M，N分别是AC，BC的中点，则EM，AN所成角的余弦值为________．

　[如图所示，过点C作CO⊥平面ABDE，垂足为O，取AB的中点F，连接CF，OF，OA，OB，则∠CFO为二面角CABD的平面角，所以cos∠CFO＝.
设AB＝1，则CF＝，OF＝，OC＝，所以O为正方形ABDE的中心．如图建立空间直角坐标系，
则E，A，M，N，
所以＝，＝，
所以cos〈，〉＝＝.]
四、解答题(本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)
17．(本小题满分10分)已知空间三点A(－2,0,2)，B(－1,1,2)，C(－3,0,4)，设a＝，b＝.
(1)若|c|＝3，且c∥，求向量c；
(2)求向量a与向量b的夹角的余弦值；
(3)若ka＋b与ka－2b互相垂直，求实数k的值．
[解]　(1)∵c∥，∴存在实数m，
使得c＝m＝m(－2，－1,2)＝(－2m，－m,2m)．
∵|c|＝3，
∴＝3|m|＝3，∴m＝±1.∴c＝(－2，－1,2)或c＝(2,1，－2)．
(2)∵a＝(1,1,0)，b＝(－1,0,2)，∴a·b＝(1,1,0)·(－1,0,2)＝－1.又∵|a|＝＝，|b|＝＝，∴cos〈a，b〉＝＝＝－，
即向量a与向量b的夹角的余弦值为－.
(3)∵ka＋b＝(k－1，k,2)，ka－2b＝(k＋2，k，－4)，∴(k－1，k,2)·(k＋2，k，－4)＝(k－1)(k＋2)＋k2－8＝0，∴k＝2或k＝－.∴当ka＋b与ka－2b互相垂直时，实数k的值为2或－.
18.(本小题满分12分)如图，在直三棱柱ABCA1B1C1中，∠ABC＝90°，BC＝2，CC1＝4，点E在线段BB1上，且EB1＝1，D，F，G分别为CC1，C1B1，C1A1的中点．

(1)求证：B1D⊥平面ABD；
(2)求证：平面EGF∥平面ABD．
[解]　如图，以B为坐标原点，BA，BC，BB1所在直线分别为x轴，y轴，z轴建立空间直角坐标系Bxyz，则

B(0,0,0)，D(0,2,2)，B1(0,0,4)．
(1)设BA＝a，则A(a,0,0)．
所以＝(a,0,0)，＝(0,2,2)，＝(0,2，－2)．
所以·＝0，
·＝0＋4－4＝0.
所以B1D⊥BA，B1D⊥BD．
又BA∩BD＝B，
所以B1D⊥平面ABD．
(2)由题意及(1)，知E(0,0,3)，G，F(0,1,4)，所以＝，＝(0,1,1)．
所以·＝0＋2－2＝0，·＝0＋2－2＝0.
所以B1D⊥EG，B1D⊥EF.
又EG∩EF＝E，
所以B1D⊥平面EGF.
由(1)，知B1D⊥平面ABD，
故平面EGF∥平面ABD．
19．(本小题满分12分)如图，已知四边形ABCD为矩形，四边形ABEF为直角梯形，FA⊥AB，AD＝AF＝FE＝1，AB＝2，AD⊥BE.

(1)求证：BE⊥DE；
(2)求点F到平面CBE的距离．
[解]　∵四边形ABCD为矩形，∴AD⊥AB，
又AD⊥BE，AB∩BE＝B，
∴AD⊥平面ABEF，
又AD⊂平面ABCD，
∴平面ABCD⊥平面ABEF.
∵FA⊥AB，平面ABCD∩平面ABEF＝AB，
∴FA⊥平面ABCD．∴FA⊥AD．
(1)证明：
如图，建立空间直角坐标系，
则B(0,2,0)，C(1,2,0)，D(1,0,0)，E(0,1,1)，F(0,0,1)，
∴＝(0，－1,1)，＝(－1,1,1)，
∴·＝0×(－1)＋(－1)×1＋1×1＝0，
∴⊥，∴BE⊥DE.
(2)由(1)得＝(1,0,0)，＝(0，－1,1)，＝(0,1,0)，
设n＝(x，y，z)是平面CBE的法向量，则由
得
令y＝1，得z＝1，∴n＝(0,1,1)是平面CBE的一个法向量．
设点F到平面CBE的距离为d，
则d＝＝＝.
∴点F到平面CBE的距离为.
20．(本小题满分12分)如图，在直三棱柱A1B1C1ABC中，AC⊥AB，AC＝AB＝4，AA1＝6，点E，F分别为CA1，AB的中点．

(1)证明：EF∥平面BCC1B1；
(2)求B1F与平面AEF所成角的正弦值．
[解]　(1)证明：如图，连接EC1，BC1，因为三棱柱A1B1C1ABC为直三棱柱，所以E为AC1的中点．
又因为F为AB的中点，所以EF∥BC1.
又EF⊄平面BCC1B1，BC1⊂平面BCC1B1，所以EF∥平面BCC1B1.
(2)以A1为原点，A1C1，A1B1，A1A所在直线分别为x、y、z轴，建立如图所示的空间直角坐标系A1xyz，

则A(0,0,6)，B1(0,4,0)，E(2,0,3)，F(0,2,6)，
所以＝(0，－2,6)，＝(2,0，－3)，＝(0,2,0)，
设平面AEF的法向量为n＝(x，y，z)，
则
令x＝3，得n＝(3,0,2)，
记B1F与平面AEF所成角为θ，则sin θ＝|cos〈，n〉|＝＝.
21．(本小题满分12分)如图所示的几何体中，BE⊥BC，EA⊥AC，BC＝2，AC＝2，∠ACB＝45°，AD∥BC，BC＝2AD．

(1)求证：AE⊥平面ABCD；
(2)若∠ABE＝60°，点F在EC上，且满足EF＝2FC，求平面FAD与平面ADC的夹角的余弦值．
[解]　(1)证明：在△ABC中，BC＝2，AC＝2，∠ACB＝45°，
由余弦定理可得AB2＝BC2＋AC2－2×BC×AC×cos 45°＝4，所以AB＝2(负值舍去)，
因为AC2＝AB2＋BC2，
所以△ABC是直角三角形，AB⊥BC．
又BE⊥BC，AB∩BE＝B，
所以BC⊥平面ABE.
因为AE⊂平面ABE，所以BC⊥AE，
因为EA⊥AC，AC∩BC＝C，
所以AE⊥平面ABCD．
(2)由题易得EB＝2AB＝4，由(1)知，BC⊥平面ABE，所以平面BEC⊥平面ABE，如图，

以B为原点，过点B且垂直于平面BEC的直线为z轴，BE，BC所在直线分别为x，y轴，建立空间直角坐标系Bxyz，则C(0,2,0)，E(4,0,0)，A(1,0，)，D(1,1，)，
因为EF＝2FC，所以F，
易知＝(0,1,0)，＝，
设平面FAD的法向量为n＝(x，y，z)，
则
即
令z＝，则x＝9，所以n＝(9,0，)．
由(1)知EA⊥平面ABCD，所以＝(－3,0，)为平面ABCD的一个法向量．
设平面FAD与平面ADC的夹角为α，
则cos α＝＝＝，
所以平面FAD与平面ADC的夹角的余弦值为.
22．(本小题满分12分)如图，在四棱锥PABCD中，底面ABCD是边长为2的菱形，∠DAB＝60°，∠ADP＝90°，平面ADP⊥平面ABCD，F为棱PD的中点．

(1)在棱AB上是否存在一点E，使得AF∥平面PCE？并说明理由；
(2)当二面角DFCB的余弦值为时，求直线PB与平面ABCD所成的角．
[解]　(1)在棱AB上存在点E，使得AF∥平面PCE，且E为棱AB的中点．
理由如下：如图，取PC的中点Q，连接EQ，FQ，
由题意得，FQ∥DC且FQ＝CD，
因为AE∥CD且AE＝CD，
所以AE∥FQ且AE＝FQ.
所以四边形AEQF为平行四边形．
所以AF∥EQ.
又EQ⊂平面PCE，AF⊄平面PCE，
所以AF∥平面PCE.
(2)连接BD，DE.由题意知△ABD为正三角形，所以ED⊥AB，即ED⊥CD，
又∠ADP＝90°，所以PD⊥AD，且平面ADP⊥平面ABCD，平面ADP∩平面ABCD＝AD，所以PD⊥平面ABCD，故以D为坐标原点建立如图所示的空间直角坐标系，

设FD＝a，则由题意知F(0,0，a)，C(0,2,0)，
B(，1,0)，
则＝(0,2，－a)，＝(，－1,0)，
设平面FBC的法向量为m＝(x，y，z)．
则
令x＝1，则y＝，z＝，
所以m＝，
易知平面DFC的一个法向量n＝(1,0,0)，
因为二面角DFCB的余弦值为，
所以|cos〈m，n〉|＝＝，即＝，解得a＝1(负值舍去)．
因为PD⊥平面ABCD，所以PB在平面ABCD内的射影为BD，
所以∠PBD为直线PB与平面ABCD所成的角，
由题意知在Rt△PBD中，tan∠PBD＝＝＝1，所以∠PBD＝45°，
所以直线PB与平面ABCD所成的角为45°.