






- 4.5.1 函数的零点与方程的解课件-2021-2022学年人教A版(2019)高一数学(必修一) 课件 1 次下载
- 4.5.2 用二分法求方程的近似解课件-2021-2022学年人教A版(2019)高一数学(必修一) 课件 1 次下载
- 4.6 章末复习提升课课件-2021-2022学年人教A版(2019)高一数学(必修一) 课件 3 次下载
- 4.5 4.5.2 用二分法求方程的近似解同步练习-2021-2022学年人教A版(2019)高一数学上册(新教材必修一) 试卷 0 次下载
- 4.4 4.4.2 第1课时 对数函数的图象和性质同步练习-2021-2022学年人教A版(2019)高一数学上册(新教材必修一) 试卷 0 次下载
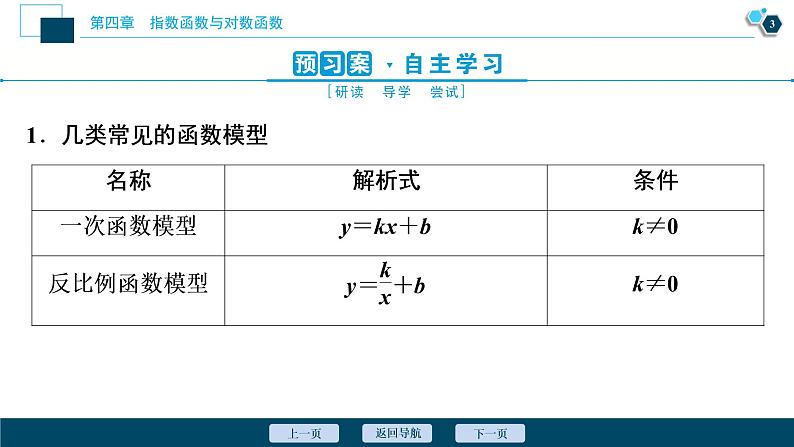
人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.5 函数的应用(二)公开课ppt课件
展开2.应用函数模型解决问题的基本过程用函数模型解应用题的四个步骤:(1)审题——弄清题意,分清条件和结论,理顺数量关系,初步选择模型;(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识建立相应的数学模型;(3)求模——求解数学模型,得出数学结论;(4)还原——将数学结论还原为实际问题.
数据拟合时,得到的函数为什么要检验?提示:因为根据已给的数据,作出散点图,根据散点图,一般是用我们比较熟悉的、最简单的函数作模型,但所选的函数模型有时可能误差较大或不切合客观实际,此时就要改选其他函数模型.
1.某种动物繁殖数量y(单位:只)与时间x(单位:年)的关系式为y=alg2(x+1).若这种动物第1年有100只,则到第7年它们发展到( )A.300只B.400只C.500只 D.600只解析:由题意可得a=100.当x=7时,y=100lg2(7+1)=300(只).
2.某种产品今年的产量是a,如果保持5%的年增长率,那么经过x年(x∈N*),该产品的产量y满足( )A.y=a(1+5%x)B.y=a+5%C.y=a(1+5%)x-1 D.y=a(1+5%)x解析:经过1年,y=a(1+5%),经过2年,y=a(1+5%)2,…,经过x年, y=a(1+5%)x.
探究点1 指数型函数模型的应用 目前我国一些高耗能低效产业(煤炭、钢铁、有色金属、炼化等)的产能过剩,将严重影响生态文明建设,“去产能”将是一项重大任务.某行业计划从2021年开始,每年的产能比上一年减少的百分比为x (0
(变问法)若本例条件不变:(1)当一条鲑鱼的耗氧量是8 100 个单位时,它的游速是多少?(2)求一条鲑鱼静止时耗氧量的单位数.
对数函数应用题的基本类型和求解策略(1)基本类型:有关对数函数的应用题一般都会给出函数的解析式,然后根据实际问题求解.(2)求解策略:首先根据实际情况求出函数解析式中的参数,或给出具体情境,从中提炼出数据,代入解析式求值,然后根据数值回答其实际意义.
函数拟合与预测的一般步骤(1)根据原始数据、表格,绘出散点图.(2)通过观察散点图,画出拟合直线或拟合曲线.(3)求出拟合直线或拟合曲线的函数关系式.(4)根据拟合误差要求判断、选择最佳拟合函数.(5)利用选取的拟合函数进行预测.(6)利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.
3.某公司制定了一个激励销售人员的奖励方案:当销售利润不超过8万元时,按销售利润的15%进行奖励;当销售利润超过8万元时,若超过A万元,则超过部分按lg5(2A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元). (1)写出奖金y关于销售利润x的函数关系式;(2)如果业务员小江获得3.2万元的奖金,那么他的销售利润是多少万元?
请做:应用案 巩固提升
数学必修 第一册4.5 函数的应用(二)课前预习ppt课件: 这是一份数学必修 第一册4.5 函数的应用(二)课前预习ppt课件,共26页。PPT课件主要包含了新知初探·课前预习,答案D,答案B,题型探究·课堂解透等内容,欢迎下载使用。
人教A版 (2019)必修 第一册4.5 函数的应用(二)图文ppt课件: 这是一份人教A版 (2019)必修 第一册4.5 函数的应用(二)图文ppt课件,共37页。PPT课件主要包含了常见函数模型,常考题型,函数模型的选择等内容,欢迎下载使用。
人教A版 (2019)必修 第一册4.5 函数的应用(二)多媒体教学课件ppt: 这是一份人教A版 (2019)必修 第一册4.5 函数的应用(二)多媒体教学课件ppt,文件包含453pptx、453DOC等2份课件配套教学资源,其中PPT共37页, 欢迎下载使用。













