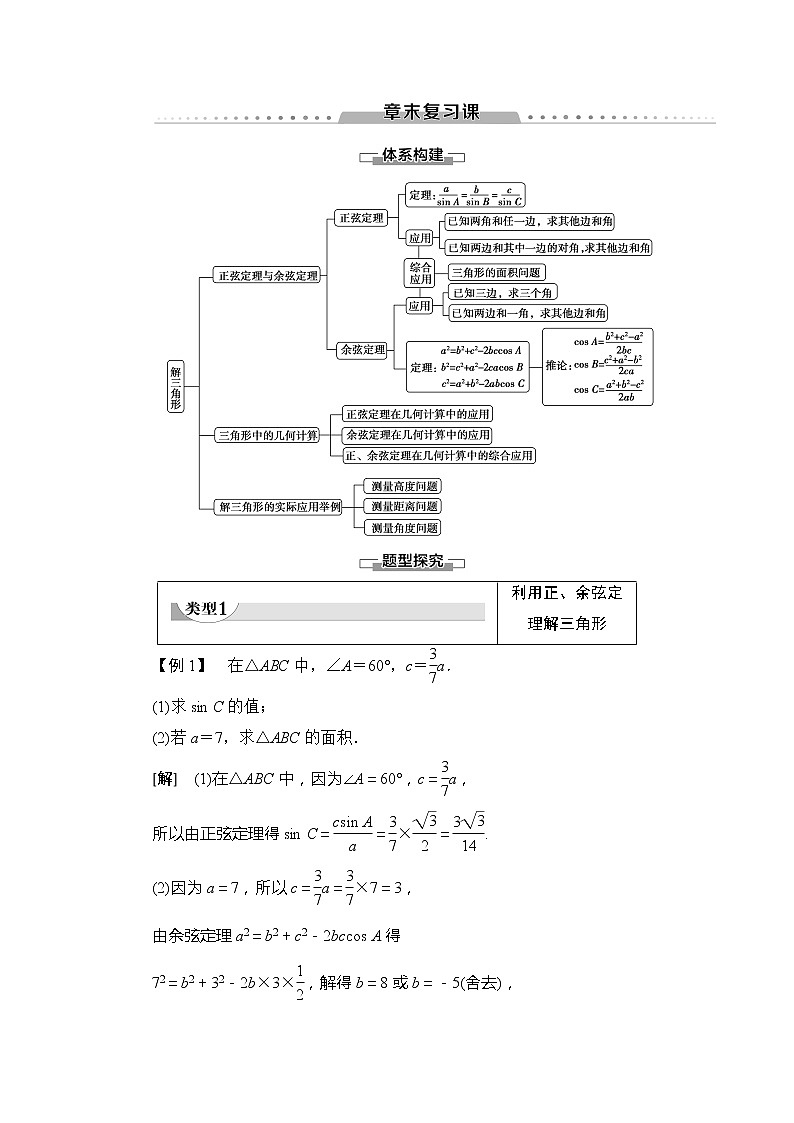
高中数学北师大版必修5第二章 解三角形综合与测试学案设计

【例1】　在△ABC中，∠A＝60°，c＝a．

(1)求sin C的值；

(2)若a＝7，求△ABC的面积．

[解]　(1)在△ABC中，因为∠A＝60°，c＝a，

所以由正弦定理得sin C＝＝×＝.

(2)因为a＝7，所以c＝a＝×7＝3，

由余弦定理a2＝b2＋c2－2bccos A得

72＝b2＋32－2b×3×，解得b＝8或b＝－5(舍去)，

所以△ABC的面积S＝bcsin A＝×8×3×＝6.

解三角形的四种类型

1．(1)在△ABC中，B＝，BC边上的高等于BC，则cos A＝(　　)

A．　　　　　　　　 B．

C．－ D．－

(2)在△ABC中，若三边的长为连续整数，且最大角是最小角的二倍，求三边长．

(1)C　[设△ABC中角A，B，C的对边分别是a，b，c，由题意可得a＝csin＝c，则a＝c．

在△ABC中，由余弦定理可得

b2＝a2＋c2－ac＝c2＋c2－3c2＝c2，则b＝C．

由余弦定理，可得cos A＝＝＝－.]

(2)[解]　设最小内角为θ，三边长为n－1，n，n＋1，

由正弦定理，得＝，

所以n－1＝，

所以cos θ＝.

由余弦定理的变形公式，得

cos θ＝，

所以＝，解得n＝5.

所以△ABC的三边分别为4,5,6.

【例2】　在△ABC中，若＝，试判断△ABC的形状．

[解]　由已知＝＝＝得＝，

以下可有两种解法：

法一：(利用正弦定理边化角)

由正弦定理得＝，

∴＝，

即sin Ccos C＝sin Bcos B，即sin 2C＝sin 2B，

∵B、C均为△ABC的内角，

∴2C＝2B或2C＋2B＝180°.

∴B＝C或B＋C＝90°，

∴△ABC为等腰三角形或直角三角形．

法二：(利用余弦定理角化边)

由余弦定理得＝，

即a2(b2－c2)＝(b2＋c2)(b2－c2)，

解得a2＝b2＋c2或b2＝c2(即b＝c)，

∴△ABC为等腰三角形或直角三角形．

1．利用正弦定理、余弦定理判断三角形的形状的两种方法

法一：通过边之间的关系判断形状；

法二：通过角之间的关系判断形状．

利用正弦、余弦定理可以将已知条件中的边、角互化，把条件化为边的关系或化为角的关系．

2．判断三角形的形状时常用的结论

(1)在△ABC中，A＞B⇔a>b⇔sin A>sin B⇔

cos A<cos B．

(2)在△ABC中，A＋B＋C＝π，A＋B＝π－C，

则cos(A＋B)＝－cos C，sin(A＋B)＝sin C．

(3)在△ABC中，a2＋b2＜c2⇔＜C＜π，a2＋b2＝c2⇔cos C＝0⇔C＝，a2＋b2>c2⇔cos C>0⇔0<C<.

2．若△ABC的三个内角满足sinA∶sinB∶sinC＝5∶11∶13，则△ABC(　　)

A．一定是锐角三角形

B．一定是直角三角形

C．一定是钝角三角形

D．可能是锐角三角形，也可能是钝角三角形

C　[根据正弦定理＝＝，

又sin A∶sin B∶sin C＝5∶11∶13，∴a∶b∶c＝5∶11∶13，

设a＝5t，b＝11t，c＝13t(t≠0)，∵c2＝a2＋b2－2abcos C，

∴cos C＝＝＝－<0，

∴角C为钝角．故选C．]

【例3】　在四边形ABCD中，BC＝a，DC＝2a，且A∶∠ABC∶C∶∠ADC＝3∶7∶4∶10，求AB的长．

[解]　如图所示，连接BD．

∵A＋∠ABC＋C＋∠ADC＝360°，

∴A＝45°，∠ABC＝105°，C＝60°，

∠ADC＝150°，

在△BCD中，由余弦定理，得

BD2＝BC2＋CD2－2BC·CDcos C

＝a2＋4a2－2a·2a·cos 60°＝3a2，

∴BD＝A．

∴BD2＋BC2＝CD2，

∴∠CBD＝90°，

∴∠ABD＝15°，

∴∠BDA＝120°.

在△ABD中，由＝，得AB＝

＝＝A．

解决三角形中的几何计算问题要注意把握三点：一是对几何图形中几何性质的挖掘，它往往是解题的切入点；二是根据条件或图形，找出已知、未知及求解中需要的三角形，合理利用正、余弦定理和三角恒等变换公式；三是要有应用方程思想解题的意识，同时还要有引入参数，突出主元，简化问题的解题意识．

3．如图所示，已知∠MON＝60°，Q是∠MON内一点，它到两边的距离分别为2和11，求OQ的长．

[解]　作QA⊥OM于A，QB⊥ON于B，连接AB，则QA＝2，QB＝11，且O，A，Q，B都在以OQ为直径的圆上．

∠AOB和∠AQB为同一弦AB所对的圆周角，且两角互补．

∵∠AOB＝60°，∴∠AQB＝120°.

在△AQB中，由余弦定理，

得AB2＝AQ2＋BQ2－2·AQ·BQ·cos∠AQB

＝22＋112－2×2×11×cos120°＝147，

∴AB＝7.

连接OQ，在Rt△OBQ中，OQ＝＝.

又在△AOB中，＝，

∴OQ＝＝14.

【例4】　在△ABC中，角A，B，C的对边分别为a，b，c，若·＝·＝1.

(1)求证：A＝B；

(2)求边长c的值；

(3)若|＋|＝，求△ABC的面积．

[解]　(1)证明：∵·＝·，

∴bccos A＝accos B，即bcos A＝acos B．

由正弦定理，得sin Bcos A＝sin Acos B，

∴sin(A－B)＝0.

∵－π<A－B<π，

∴A－B＝0，即A＝B．

(2)∵·＝1，∴bccos A＝1.

由余弦定理，得bc×＝1，

即b2＋c2－a2＝2.

∵由(1)，得a＝b，∴c2＝2，∴c＝.

(3)∵|＋|＝，

∴||2＋||2＋2·＝6，

即∵c2＋b2＋2＝6，∵c2＋b2＝4，∴c2＝2，∴b2＝2，b＝.

∴△ABC为正三角形．

∴S△ABC＝×××sin 60°＝.

在高考中解三角形问题常与平面向量知识(主要是数量积)结合在一起进行考查．判断三角形形状或结合正弦定理、余弦定理求值，这也是高考命题的新趋势．

4．在△ABC中，角A，B，C所对的边分别是a，b，c，若sin2B＋sin2C＝sin2A＋sin Bsin C，且·＝4，求△ABC的面积S.

[解]　由已知得b2＋c2＝a2＋bc，

∴bc＝b2＋c2－a2＝2bccos A，∴cos A＝，sin A＝.

由·＝4，得bccos A＝4，∴bc＝8.

∴S＝bcsin A＝2.

[探究问题]

1．在△ABC中，由a2＋b2－c2＝－ab可得到什么？

[提示]　由a2＋b2－c2＝－ab得＝－，即cos C＝－，故C＝120°.

2．在△ABC中，若A＋B＝，能否求出sin A＋sin B的范围？

[提示]　用角B表示角A得B＝－A，则sin A＋sin B＝sinA＋sin，化为一个角的三角函数可求其范围．

【例5】　在△ABC中，设角A，B，C的对边分别为a，b，c，已知cos2A＝sin2B＋cos2C＋sin Asin B．

(1)求角C的大小；  (2)若c＝，求△ABC周长的取值范围．

思路探究：(1)利用正弦定理把角转化为边，然后利用余弦定理求角C；(2)利用正弦定理得到周长的表达式化为一个角的三角函数求范围．

[解]　(1)由题意知1－sin2A＝sin2B＋1－sin2C＋sin Asin B，

即sin2A＋sin2B－sin2C＝－sin Asin B，

由正弦定理得a2＋b2－c2＝－ab，

由余弦定理得cos C＝＝＝－，

又∵0<C<π，∴C＝.

(2)由正弦定理得＝＝＝2，

∴a＝2sin A，b＝2sin B，

则△ABC的周长为L＝a＋b＋c＝2(sin A＋sin B)＋

＝2＋＝2sin＋.

∵0<A<，∴＜A＋＜，∴<sin≤1，∴2<2sin＋≤2＋，

∴△ABC周长的取值范围是(2，2＋]．

1．(变结论)例5的条件不变，若c＝2，a＝，求sin 2B的值．

[解]　由例5的解答可知C＝，由正弦定理

＝，即sin A＝＝＝，

由于c＞a，故A是锐角，cos A＝＝，

所以sin 2A＝2sin Acos A＝，

cos 2A＝2cos2A－1＝－，

得sin 2B＝sin 2＝sin＝cos 2A＋sin 2A＝×＋×＝.

2．(变条件)把例5的条件换为“2ccos B＝2a＋b”，求角C．

[解]　由正弦定理及2ccos B＝2a＋b得

2sin Ccos B＝2sin A＋sin B，因为A＋B＋C＝π，

所以sin A＝sin(B＋C)，则2sin Ccos B＝2sin(B＋C)＋sin B，

即2sin Bcos C＋sin B＝0，又0＜B＜π，

所以sin B＞0，

则cos C＝－，又C∈(0，π)，故C＝.

与三角形有关的综合问题的解法

该类问题以三角形为载体，在已知条件中设计了三角形的一些边角关系，由于正弦定理和余弦定理都是关于三角形的边角关系的等式，通过定理的运用能够实现边角互化，在边角互化时，经常用到三角函数中两角和与差的公式及倍角公式等．