初中第二十二章 二次函数综合与测试练习

这是一份初中第二十二章 二次函数综合与测试练习，共19页。试卷主要包含了二次函数y＝2，二次函数y＝，已知二次函数y＝﹣等内容，欢迎下载使用。
【二次函数】单元质量检测
一．选择题
1．二次函数y＝2（x﹣2）2﹣5的顶点坐标是（　　）
A．（﹣2，5） B．（2，5） C．（﹣2，﹣5） D．（2，﹣5）
2．二次函数y＝（x+1）2﹣3的对称轴为直线（　　）
A．x＝3 B．x＝﹣3 C．x＝1 D．x＝﹣1
3．若二次函数y＝ax2+bx+c（a≠0）的x与y的部分对应值如下表：
x
﹣2
﹣1
0
1
2
3
y
14
7
2
﹣1
﹣2
﹣1
则当x＝5时，y的值为（　　）
A．﹣1 B．2 C．7 D．14
4．已知二次函数y＝﹣（x﹣2）2+3，且﹣1≤x≤1，下列说法正确的是（　　）
A．此函数的最大值为3
B．当x＝﹣1时，函数有最大值﹣6
C．函数y的取值范围是2≤y≤3
D．函数y的取值范围是﹣6≤y≤2
5．某商品的进价为每件60元，现在的售价为每件80元，每星期可卖出200件．市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件．则每星期售出商品的利润y（单位：元）与每件涨价x（单位：元）之间的函数关系式是（　　）
A．y＝200﹣10x B．y＝（200﹣10x）（80﹣60﹣x）
C．y＝（200+10x）（80﹣60﹣x） D．y＝（200﹣10x）（80﹣60+x）
6．二次函数y＝x2，当﹣1≤x≤3时，函数值y的取值范围是（　　）
A．1≤y≤9 B．0≤y≤9 C．0≤y≤1 D．y≥0
7．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：
（1）abc＞0；（2）b＜a+c；（3）4a+2b+c＞0；（4）2c＜3b；（5）a+b＞m（am+b）（m≠1的实数）．其中正确的的结论有（　　）

A．2个 B．3个 C．4个 D．5个
二．填空题
8．二次函数y＝x2的图象开口方向是 　 　（填“向上”或“向下”）．
9．把抛物线y＝2x2+1向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为 　 　．
10．将二次函数y＝2x2﹣4x﹣1的图象沿着y轴翻折，所得到的图象对应的函数表达式是　 　．
11．抛物线y＝﹣x2+bx+c的部分图象如图所示，其对称轴是x＝﹣1，若y≥3，则x的取值范围是 　 　．

12．如图，二次函数y＝﹣x2+4x+c的图象的顶点为A，与y轴的交点为B，BC∥x轴，交抛物线于点C，则△ABC的面积是 　 　．

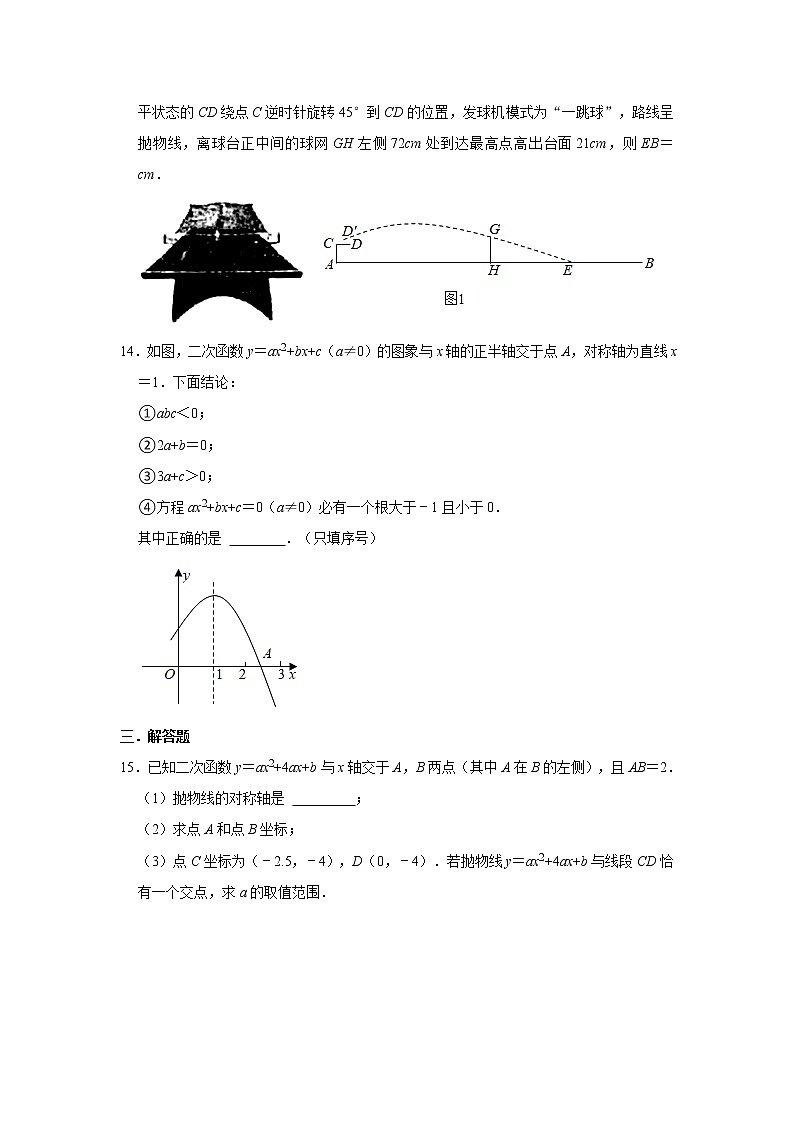
13．某校购买了一套乒乓球桌和自动发球机，侧面如图1所示，球台长度AB＝274cm，发球机紧贴球台端线点A处，高出球台的部分AC＝12cm，出球管道CD＝5cm，若将水平状态的CD绕点C逆时针旋转45°到CD的位置，发球机模式为“一跳球”，路线呈抛物线，离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm，则EB＝　 　cm．

14．如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴的正半轴交于点A，对称轴为直线x＝1．下面结论：
①abc＜0；
②2a+b＝0；
③3a+c＞0；
④方程ax2+bx+c＝0（a≠0）必有一个根大于﹣1且小于0．
其中正确的是 　 　．（只填序号）

三．解答题
15．已知二次函数y＝ax2+4ax+b与x轴交于A，B两点（其中A在B的左侧），且AB＝2．
（1）抛物线的对称轴是 　 　；
（2）求点A和点B坐标；
（3）点C坐标为（﹣2.5，﹣4），D（0，﹣4）．若抛物线y＝ax2+4ax+b与线段CD恰有一个交点，求a的取值范围．





16．抛物线y＝ax2+bx+4（a≠0）交x轴于A（﹣1，0）、B（4，0）两点，D是抛物线上的一点，且点D的横坐标为1，连接AD，P是线段AD上的动点．
（1）求a，b的值；
（2）过点P作PH∥y轴，交抛物线于点H，当PH＝时，求点P的坐标．




17．一商店销售某种商品，平均每天可售出20件，每件盈利50元，为了扩大销售、增加利润，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．
（1）当每件商品降价多少元时，该商店每天销售利润为1600元？
（2）当每件商品降价多少元时，该商店每天销售利润最大？最大为多少元？




18．如图，已知抛物线y＝x2+bx+c的图象与x轴的一个交点为A（1，0），另一个交点为B，且与y轴交于点C（0，5）．
（1）求该抛物线对应的函数表达式；
（2）求直线BC对应的函数表达式；
（3）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值．





19．已知抛物线y＝x2+bx+c与x轴交于A（x1，0），B（x2，0）两点，且x1＜x2，若x22+3x12＝3k（k为正整数），我们把该抛物线称为“B系抛物线”．
特例感知：
（1）当b＝2，c＝﹣15时，请判断抛物线y＝x2+bx+c是否是“B系抛物线”，并说明理由．
推广验证：
（2）若c＝﹣b2，且b为负整数，请判断抛物线y＝x2+bx+c是否是“B系抛物线”，并说明理由．
拓展应用：
（3）在（2）的条件下，若M为该抛物线的顶点，且△ABM为等腰直角三角形，求该抛物线的解析式．




20．如图，在直角坐标系中，O为坐标原点，抛物线的顶点为M（2，﹣），抛物线与x轴的一个交点为A（4，0），点B（2，2）与点C关于y轴对称．
（1）判断点C是否在该抛物线上，并说明理由；
（2）顺次连接AB，BC，CO，判断四边形ABCO的形状并证明；
（3）设点P是抛物线上的动点，连接PA、PC、AC，△PAC的面积S随点P的运动而变化，请探究S的大小变化并填写表格①～④处的内容；当S的值为②时，求点P的横坐标的值．
直线AC的函数表达式
S取的一个特殊值
满足条件的P点的个数
S的可能取值范围
①　 　
6
4个
③　 　
②　 　
3个
\
10
2个
④　 　


参考答案
一．选择题
1．解：∵抛物线y＝a（x+h）2+k的顶点坐标是（﹣h，k），
∴抛物线y＝2（x﹣2）2﹣5的顶点坐标是（2，﹣5）．
故选：D．
2．解：∵抛物线y＝a（x+h）2+k的对称轴是直线x＝﹣h，
∴抛物线y＝（x+1）2﹣3的对称轴是直线x＝﹣1．
故选：D．
3．解：由表格可知，当x＝1时，y＝﹣1，当x＝3时，y＝﹣1，
由抛物线的对称性可知，抛物线的对称轴为直线x＝2；
∴x＝5时y的值与x＝﹣1时的值相等，
∴x＝5时y的值为7．
故选：C．
4．解：A、二次函数y＝﹣（x﹣2）2+3，当x＝2时，最大值为3，但x＝2不满足﹣1≤x≤1，故不符合题意；
B、抛物线y＝﹣（x﹣2）2+3的对称轴为直线x＝2，且﹣1＜0，开口向下，在﹣1≤x≤1时，y随x的增大而增大，因此x＝1时，函数最大值为2，故不符合题意；
C、二次函数y＝﹣（x﹣2）2+3，在﹣1≤x≤1时，y随x的增大而增大，而x＝﹣1时，y＝﹣6，x＝1时，y＝2，所以函数y的取值范围是﹣6≤y≤2，故不符合题意；
D、由以上分析知，当﹣1≤x≤1时，函数y＝﹣（x﹣2）2+3的取值范围是﹣6≤y≤2，故符合题意；
故选：D．
5．解：∵每涨价1元，每星期要少卖出10件，每件涨价x元，
∴销售每件的利润为（80﹣60+x）元，每星期的销售量为（200﹣10x），
∴每星期售出商品的利润y＝（200﹣10x）（80﹣60+x）．
故选：D．
6．解：∵二次函数y＝x2，
∴当x＝0时，y有最小值是0，
∵当x＝﹣1时，y＝1，当x＝3时，y＝9，
∴当﹣1≤x≤3时，函数值y的取值范围是0≤y≤9，
故选：B．
7．解：（1）图象开口向下，与y轴交于正半轴，对称轴为x＝1，能得到：a＜0，c＞0，﹣＝1，
∴b＝﹣2a＞0，
∴abc＜0，此结论错误；
②当x＝﹣1时，由图象知y＜0，
把x＝﹣1代入解析式得：a﹣b+c＜0，
∴b＞a+c，
∴此结论错误；
③图象开口向下，与y轴交于正半轴，对称轴为x＝1，
能得到：a＜0，c＞0，﹣＝1，
所以b＝﹣2a，
所以4a+2b+c＝4a﹣4a+c＞0，
∴此结论正确；
④∵由①②知b＝﹣2a且b＞a+c，
∴2c＜3b，此结论正确；
⑤当x＝1时，y＝a+b+c，
当x＝m时，y＝am2+bm+c，
∵m≠1的实数，图象开口向下，对称轴为x＝1，
∴a+b+c＞am2+bm+c，
∴a+b＞m（am+b），
∴此结论正确．
故选：B．
二．填空题
8．解：由y＝x2得：a＞0，
∴二次函数图象开口向上．
故答案为：向上．
9．解：把抛物线y＝2x2+1向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为：y＝2（x+1）2+1﹣3，即y＝2x2+4x
故答案为y＝2x2+4x．
10．解：将二次函数y＝2x2﹣4x﹣1的图象沿着y轴翻折，所得到的图象对应的函数表达式是y＝2（﹣x）2﹣4•（﹣x）﹣1，即y＝2x2+4x﹣1，
故答案为y＝2x2+4x﹣1，
11．解：由图象可得抛物线对称轴为直线x＝﹣1，
∵抛物线经过点（0，3），
由对称性可得抛物线经过点（﹣2，3），
∴y≥3时x的取值范围是﹣2≤x≤0．
故答案为：﹣2≤x≤0．
12．解：∵抛物线y＝﹣x2+4x+c＝﹣（x﹣3）2+6+c，
∴顶点坐标A为（3，6+c），对称轴为直线x＝3，
∴BC＝6，
当x＝0时y＝c，
∴点B坐标为（0，c），
∴S△ABC＝BC（yA﹣yB）＝6（6+c﹣c）＝18．
故答案为：18．
13．解：以AC为y轴，以AB为x轴，A为原点建立平面直角坐标系，如图，

设抛物线最高点为N，对称轴MN与x轴交于M，则MN＝21，
∴AB＝274，
∵GH是AB正中间，
∴AH＝AB＝137，
∴AM＝AH﹣MH＝137﹣72＝65，
设抛物线为：y＝a（x﹣65）2+21（a＜0），
过D′作D′P⊥x轴交CD于点Q，交x轴于点P，
则∠CQD′＝∠APQ＝90°，
∵旋转45°，
∴CD′＝CD＝5，
CQ＝D′Q＝CD′cos∠D′CD＝5，
∴D′P＝D′Q+PQ＝5+12＝17，
∴D′（5，17）代入抛物线得：
a×（5﹣65）2+21＝17，
∴a＝﹣，
∴y＝﹣（x﹣65）2+21，
令y＝0，则﹣（x﹣65）2+21＝0，
解得：x1＝65+30，x2＝65﹣30（舍去），
∴E（65+30，0），
∴EB＝AB﹣AE＝274﹣（65+30）＝（209﹣30）（cm），
故答案为：（209﹣30）．
14．解：由图象可得，
a＜0，b＞0，c＞0，
则abc＜0，故①正确；
∵﹣＝1，
∴b＝﹣2a，
∴2a+b＝0，故②正确；
∵函数图象与x轴的正半轴交点在点（2，0）和（3，0）之间，对称轴是直线x＝1，
∴函数图象与x轴的另一个交点在点（0，0）和点（﹣1，0）之间，故④正确；
∴当x＝﹣1时，y＝a﹣b+c＜0，
∴y＝a+2a+c＜0，
∴3a+c＜0，故③错误；
故答案为：①②④．
三．解答题
15．解：（1）∵二次函数y＝ax2+4ax+b，
∴抛物线对称轴为直线x＝﹣＝﹣2，
故答案为：x＝﹣2；
（2）∵抛物线对称轴为直线x＝﹣2，
A、B是抛物线与x轴的交点，且AB＝2，
∴A点坐标（﹣3，0），B点坐标（﹣1，0）；
（3）把B点坐标代入y＝ax2+4ax+b，得：a﹣4a+b＝0，
即b＝3a，
∴y＝ax2+4ax+3a＝a（x+2）2﹣a，
∴抛物线顶点坐标为（﹣2，﹣a），
∵C（﹣2.5，﹣4），D（0，﹣4），
∴线段CD的解析式为y＝﹣4（﹣2.5≤x≤0），
若y＝ax2+4ax+3a与线段CD恰有一个交点，
当a＞0时，
①线段CD恰过抛物线顶点，

∴﹣a＝﹣4，即a＝4；
②当x＝﹣2.5时，

a+4a（﹣）+3a＜﹣4，
解得：a＞；
当a＜0时，

3a≤﹣4，即a≤﹣，
综上：a＝4或a＞或a≤﹣．
16．解：（1）由题意得：，
解得，
∴a＝﹣1，b＝3；
（2）由（1）可知抛物线的表达式为y＝﹣x2+3x+4，
∵D是抛物线上的一点，且点D的横坐标为1，
∴y＝﹣1+3+4＝6，
∴D（1，6），
设直线AD的解析式为y＝kx+m，
∴，
∴，
∴直线AD的解析式为y＝3x+3，
设P（n，3n+3）（﹣1＜n＜1），则H（n，﹣n2+3n+4），
∴PH＝﹣n2+3n+4﹣（3n+3）＝﹣n2+1，
∴﹣n2+1＝，
解得n1＝，n2＝﹣，
∴点P的坐标为（+3）或（﹣+3）．
17．解：（1）设每件商品降价x元时，该商品每天的销售利润为1600元，
由题意得：（50﹣x）（20+2x）＝1600，
整理得：x2﹣40x+300＝0，
∴（x﹣10）（x﹣30）＝0，
∴x1＝10，x2＝30，
∵每件盈利不少于25元，
∴x2＝30应舍去．
答：每件商品降价10元时，该商品每天的销售利润为1600元；
（2）设每件商品降价n元时，该商店每天销售利润为y元，
则：y＝（50﹣n）（20+2n）＝﹣2（n﹣20）2+1800，
∵a＝﹣2＜0，
∴y有最大值，
当n＝20时，y有最大值＝1800元，
即当每件商品降价20元时，该商店每天销售利润最大值为1800元．
18．解：（1）由题可得，抛物线过点A（1，0），C（0，5），
把点A和C代入抛物线的解析式，得：
，
解得：，
∴抛物线的解析式为y＝x2﹣6x+5；
（2）当y＝0，则x2﹣6x+5＝0，
解得x1＝1，x2＝5，
所以点B（5，0），
设直线BC的解析式为y＝kx+m，
把点B和C代入解析式得：
，
解得：，
∴直线BC的解析式为y＝﹣x+5；
（3）设M（x，x2﹣6x+5）（1＜x＜5），
∵MN∥y轴，
∴N（x，﹣x+5），
∴MN＝﹣x+5﹣x2+6x﹣5＝，
∴MN在处取得最大值，最大值为．

19．解：（1）当b＝2，c＝﹣15时，代入y＝x2+bx+c，即y＝x2+2x﹣15，
令y＝0，即0＝x2+2x﹣15，
∴（x﹣3）（x+5）＝0，
∴x1＝﹣5，x2＝3，
∴，
即k＝28，为正整数，
∴该抛物线是“B系抛物线”；
（2）∵c＝﹣b2，
∴y＝x2+bx﹣b2，
令y＝0，即，
∴，
∵b为负整数，
∴，，
∴，即3b2＝3k，此时k＝b2，
∴是“B系抛物线”；
（3）如图，当△ABM为等腰直角三角形时，过M作MH⊥AB，其中AB＝﹣2b，点M横坐标为，

将代入，
即，
∴MH＝b2，
∵△ABM为等腰直角三角形，
∴，
∴，
解得：b1＝0（舍去），b2＝﹣1，
∴抛物线的解析式．
20．解：（1）设抛物线解析式为y＝a（x﹣2）2﹣，将A（4，0）代入，
得：0＝a（4﹣2）2﹣，
解得：a＝，
∴抛物线解析式为y＝（x﹣2）2﹣＝x2﹣x，
∵点B（2，2）与点C关于y轴对称，
∴C（﹣2，2），
当x＝﹣2时，y＝（﹣2﹣2）2﹣＝2，
∴点C在该抛物线y＝（x﹣2）2﹣上；
（2）四边形ABCO是菱形．
证明：∵B（2，2），C（﹣2，2），
∴BC∥x轴，BC＝2﹣（﹣2）＝4，
∵A（4，0），
∴OA＝4，
∴BC＝OA，
∴四边形ABCO是平行四边形，
∵OC＝＝4，
∴OC＝OA，
∴四边形ABCO是菱形．
（3）①设直线AC的函数表达式为y＝kx+b，
∵A（4，0），C（﹣2，2），
∴，
解得：，
∴直线AC的函数表达式为y＝x+；
故答案为：y＝x+；
②当点P在直线AC下方的抛物线上时，如图2，
设P（t，t2﹣t），过点P作PH∥y轴交直线AC于点H，
则H（t，t+），
∴PH＝t+﹣（t2﹣t）＝﹣t2+t+，
∵满足条件的P点有3个，
∴在直线AC下方的抛物线上只有1个点P，即S△PAC的值最大，
∵S△PAC＝S△PHC+S△PHC＝PH•[4﹣（﹣2）]＝3PH＝3（﹣t2+t+）＝（t﹣1）2+，
∴当t＝1时，S△PAC取得最大值，
故答案为：；
③由②知，当0＜S＜时，在直线AC下方的抛物线上有2个点P，满足S△PAC＝S，
在直线AC上方的抛物线上一定有2个点P，满足S△PAC＝S，
∴满足条件S△PAC＝S的P点有4个，符合题意．
故答案为：0＜S＜；
④∵满足条件S△PAC＝S的P点只有2个，而在直线AC上方的抛物线上一定有2个点P，满足S△PAC＝S，
∴在直线AC下方的抛物线上没有点P，满足S△PAC＝S，
由②知，当S＞时，在直线AC下方的抛物线上没有点P，满足S△PAC＝S，符合题意．
故答案为：S＞．