




2021学年第26章 二次函数26.2 二次函数的图象与性质3. 求二次函数的表达式示范课ppt课件
展开二次函数的表达形式二次函数的表达形式
求函数的表达式求函数的表达式
仔细观察,领悟实质仔细观察,领悟实质
求二次函数的表达式求二次函数的表达式
问题1:一个二次函数的图象经过(0,1)、(2,4)、(3,10)三点,求这个二次函数的解析式。
(2)解这个方程组得:
(3)你能写出这个二次函数的解析式吗?
故这个二次函数的解析式为:
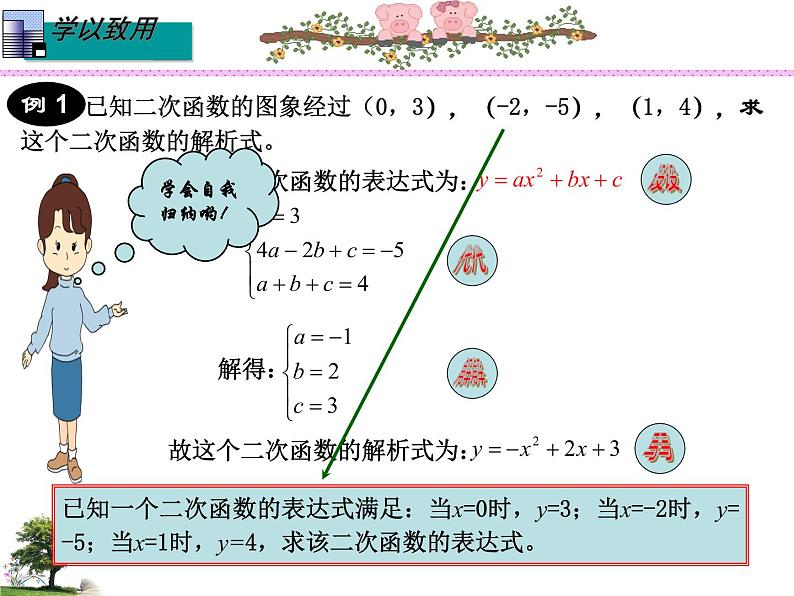
已知一个二次函数的表达式满足:当x=0时,y=3;当x=-2时,y=-5;当x=1时,y=4,求该二次函数的表达式。
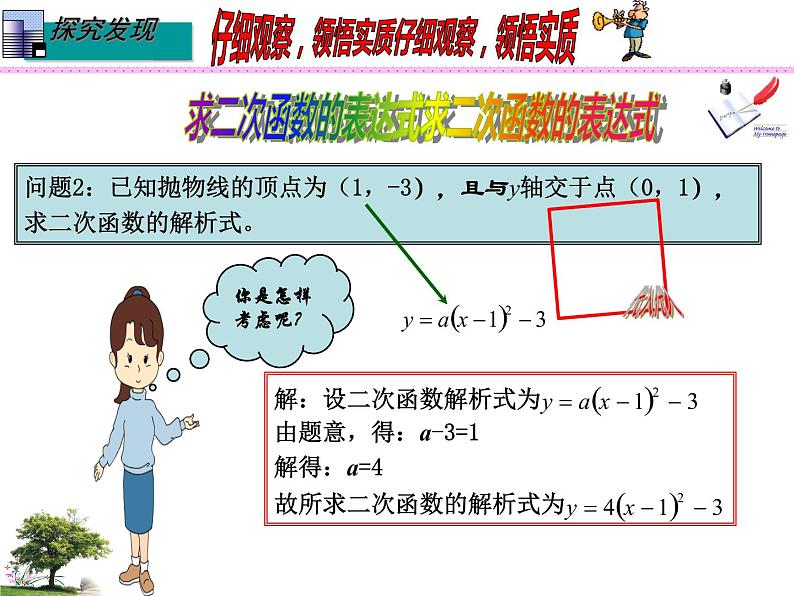
问题2:已知抛物线的顶点为(1,-3),且与y轴交于点(0,1),求二次函数的解析式。
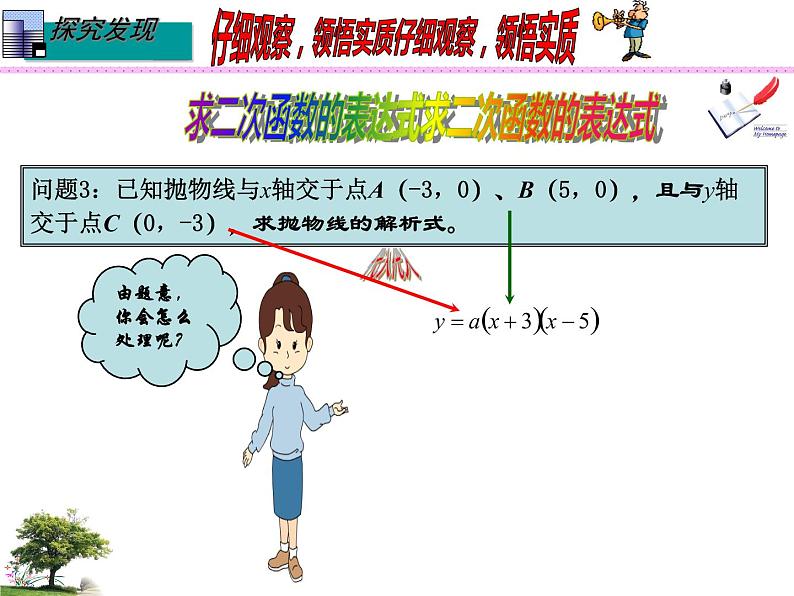
问题3:已知抛物线与x轴交于点A(-3,0)、B(5,0),且与y轴交于点C(0,-3),求抛物线的解析式。
由题意,你会怎么处理呢?
二次函数的解析式的三种形式二次函数的解析式的三种形式
归纳总结,领悟精髓归纳总结,领悟精髓
已知抛物线顶点坐标和另一个点的坐标。
已知抛物线与x轴的两个交点坐标及另一个点的坐标。
用待定系数法求二次函数解析式的步骤用待定系数法求二次函数解析式的步骤
(Ⅰ)设出适当的二次函数解析式形式;
(Ⅱ)代入点的坐标构成方程(组);
(Ⅲ)解方程(组)求出待定系数的值;
(Ⅳ)写出二次函数的解析式并化为一般形式。
(1)求该抛物线的表达式;
(2)在(1)中的抛物线上对称轴上是否存在点D,使AD+CD的值最小, 若存在,求出点D的坐标,若不存在,请说明理由。
(3)在(1)中的抛物线上是否存在一点E,使△ABE的面积为10,若存 在,求出点E的坐标。
(4)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面 积最大?若存在,求出点P的坐标及△PBC的面积最大值。若不存在, 请说明理由。
根据下列条件,求二次函数的表达式:
(2)二次函数的图象过A、B、C三点,点A的坐标为(-1,0), 点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(3)当x=-1时,抛物线的最高点的纵坐标为4,且与x轴两交点之 间的距离为6.
2.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),以x轴交于C、D两点,点P是x轴上的一个动点。
(1)求此抛物线对应的函数表达式;(2)当PA+PB的值最小时,求点P的坐标。
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
数学九年级下册3. 求二次函数的表达式教课内容课件ppt: 这是一份数学九年级下册<a href="/sx/tb_c21370_t3/?tag_id=26" target="_blank">3. 求二次函数的表达式教课内容课件ppt</a>,共24页。PPT课件主要包含了复习引入,导入新课,待定系数法,典例精析,c-5,探究归纳,针对训练,a-1,b-6,归纳总结等内容,欢迎下载使用。
初中数学华师大版九年级下册3. 求二次函数的表达式作业ppt课件: 这是一份初中数学华师大版九年级下册<a href="/sx/tb_c21370_t3/?tag_id=26" target="_blank">3. 求二次函数的表达式作业ppt课件</a>,共16页。PPT课件主要包含了y=2x2-3x+1,y=x2+2x-8等内容,欢迎下载使用。
初中数学华师大版九年级下册3. 求二次函数的表达式图片课件ppt: 这是一份初中数学华师大版九年级下册3. 求二次函数的表达式图片课件ppt,共37页。PPT课件主要包含了逐点学练,本节小结,作业提升,本节要点,学习流程,知识点,二次函数的简单应用,求二次函数的表达式等内容,欢迎下载使用。













