2022高三数学（理科）（全国版）一轮复习课件：第8章第3讲 直线、平面平行的判定及性质

这是一份2022高三数学（理科）（全国版）一轮复习课件：第8章第3讲 直线、平面平行的判定及性质，共22页。PPT课件主要包含了考点帮·必备知识通关，考法帮·解题能力提升，考情解读，图8-3-2，图8-3-3，图8-3-4，图8-3-6，图8-3-7等内容，欢迎下载使用。

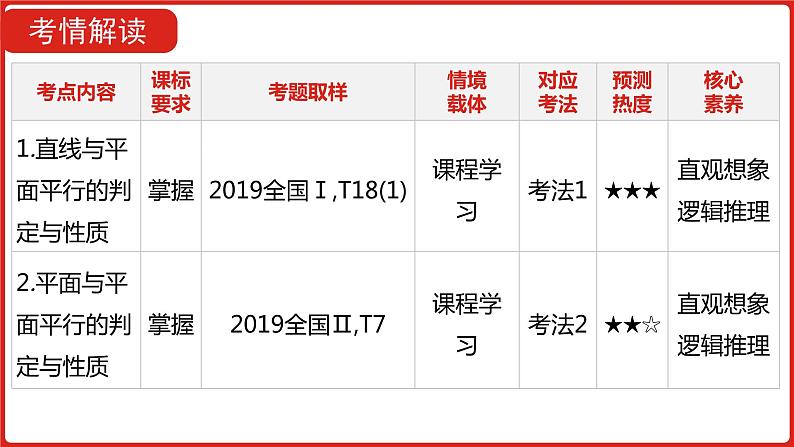
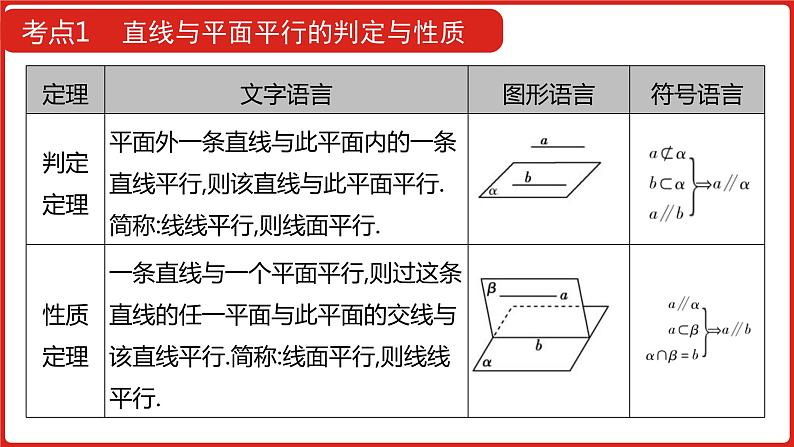
考点1 直线与平面平行的判定与性质
考点2 平面与平面平行的判定与性质
考法1 线面平行的判定与性质
考法2 面面平行的判定与性质
考点1 直线与平面平行的判定与性质考点2 平面与平面平行的判定与性质
考点1 直线与平面平行的判定与性质
注意 (1)在推证线面平行时,一定要强调直线a不在平面内,直线b在平面内,且a∥b,否则会出现错误.(2)一条直线平行于一个平面,它可以与平面内的无数条直线平行,但这条直线与平面内的任意一条直线可能平行,也可能异面.
考点2 平面与平面平行的判定与性质
规律总结 平行关系中常用的结论1.垂直于同一条直线的两个平面平行.2.平行于同一平面的两个平面平行.3.垂直于同一平面的两条直线平行.4.两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.5.夹在两个平行平面之间的平行线段长度相等.6.经过平面外一点有且只有一个平面与已知平面平行.
考法1 线面平行的判定与性质考法2 面面平行的判定与性质
考法1 线面平行的判定与性质
解析 (1)解法一(利用线面平行的判定定理) 如图8-3-3,取PA的中点M,连接ME,MF.
因为F为PB的中点,所以FG∥PA,又FG⊄平面PAE,PA⊂平面PAE,所以FG∥平面PAE. 因为E为DC中点,所以EC∥AG且EC=AG,所以四边形AGCE为平行四边形,所以CG∥EA.因为CG⊄平面PAE,EA⊂平面PAE,所以CG∥平面PAE.又CG∩FG=G,所以平面CFG∥平面PAE.因为CF⊂平面CFG,所以CF∥平面PAE.(把握好线线、线面、面面关系的转化)(2)在正方形ABCD中,BC⊥AB,因为∠PBC=90°,所以BC⊥PB.又AB∩PB=B,所以BC⊥平面ABP.
方法技巧1.证明直线与平面平行的常用方法(1)利用线面平行的定义.(2)利用线面平行的判定定理:关键是在平面内找与已知直线平行的直线,可先直观判断题中是否存在这样的直线,若不存在,则需作出直线,常考虑利用三角形的中位线、平行四边形的对边平行或过已知直线作一平面,找两平面的交线进行证明.(3)利用面面平行的性质定理:①直线在一平面内,由两平面平行,推得线面平行,即α∥β,a⊂α⇒a∥β.
②直线在两平行平面外,且与其中一平面平行,则这条直线与另一平面平行,即α∥β,a∥α,a⊄β⇒a∥β.2.线面平行性质的应用证明线线平行,常常将线面平行转化为该线与过该线的一个平面和已知平面的交线平行.注意 应用线面平行的判定定理和性质定理时,一定要注意定理成立的条件,通常应严格按照定理成立的条件规范书写步骤.
考法2 面面平行的判定与性质
示例2 如图8-3-6,四边形ABCD是边长为3的正方形,ED⊥平面ABCD, AF⊥平面ABCD, DE=3AF=3.(1)证明:平面ABF∥平面DCE.(2)在DE上是否存在一点G,使平面FBG将几何体ABCDEF分成的上、下两部分的体积比为3∶11?若存在,求出点G的位置;若不存在,请说明理由.
解析 (1)解法一(应用面面平行的判定定理证明) 因为DE⊥平面ABCD, AF⊥平面ABCD,所以DE∥AF.因为AF⊄平面DCE,DE⊂平面DCE,所以AF∥平面DCE.
因为四边形ABCD是正方形,所以AB∥CD.因为AB⊄平面DCE,CD⊂平面DCE,所以AB∥平面DCE.因为AB∩AF=A, AB⊂平面ABF,AF⊂平面ABF,所以平面ABF∥平面DCE.解法二(利用垂直于同一条直线的两个平面平行证明) 因为DE⊥平面ABCD,所以DE⊥AD,在正方形ABCD中,AD⊥DC.又DE∩DC=D,DE⊂平面DCE,DC⊂平面DCE,所以AD⊥平面DCE.同理AD⊥平面ABF.所以平面ABF∥平面DCE.(2)假设存在满足题意的点G,如图8-3-7,过G作MG∥BF交EC于点M,连接BG,BM,GF,BD.
方法技巧1.证明面面平行的常用方法(1)利用面面平行的定义.(2)利用面面平行的判定定理.(3)利用垂直于同一条直线的两个平面平行(l⊥α,l⊥β⇒α∥β).(4)利用平面平行的传递性(α∥β,β∥γ⇒α∥γ).(5)利用“线线平行”“线面平行”“面面平行”的相互转化.2.面面平行的性质的应用(1)两平面平行,构造与之相交的第三个平面,可得交线平行.