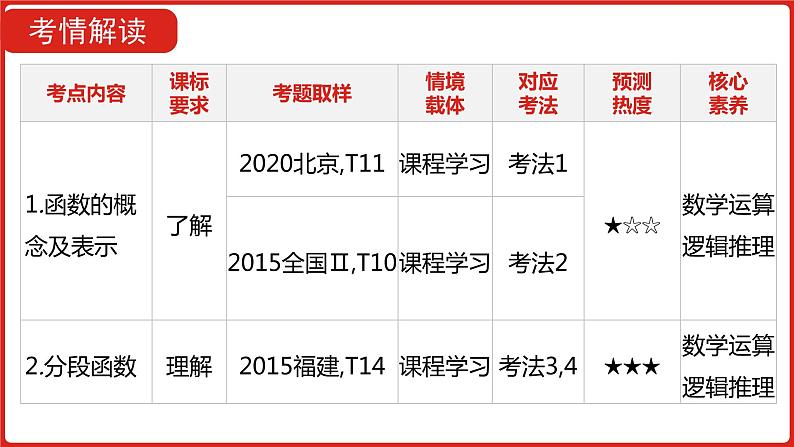
2022高三数学（理科）（全国版）一轮复习课件：第2章第1讲 函数及其表示

这是一份2022高三数学（理科）（全国版）一轮复习课件：第2章第1讲 函数及其表示，共39页。PPT课件主要包含了考点帮·必备知识通关，考点2分段函数，考法帮·解题能力提升，提能力∙数学探索，考情解读，函数的概念，函数的表示法，思维导引等内容，欢迎下载使用。

考点1 函数的概念及表示
考法1 求函数的定义域
考法2 求函数的解析式
考法3 已知定义域（值域）求参数的值或取值范围考法4 分段函数的应用
高分帮 ·“双一流”名校冲刺
通思想∙ 方法指导
数学探索 与函数有关的新定义问题
思想方法 分类与整合思想在函数中的应用
考点1 函数的概念及表示考点2 分段函数
考点1 函数的概念及表示
2.构成函数的三要素在函数y=f(x),x∈A中,自变量 x的取值范围A叫作定义域,与x的值对应的y值叫作函数值,函数值的集合{f(x)|x∈A}叫作值域.定义域、对应关系、值域是构成函数的三要素. 注意 两个函数当且仅当定义域和对应关系相同时,才是相同函数,若是值域和对应关系相同,两函数不一定相同.
考点2 分段函数
在函数的定义域内,对于自变量x取值的不同区间,有着不同的对应关系,这样的函数称为分段函数.分段函数的定义域是各段定义区间的并集,值域是各段函数值区间的并集.注意 分段函数虽由几个部分构成,但它表示的是一个函数,各部分函数定义区间不可以相交.
考法1 求函数的定义域考法2 求函数的解析式考法3 已知定义域（值域）求参数的值 或取值范围考法4 分段函数的应用
考法1 求函数的定义域
方法技巧 求抽象函数定义域的方法(1)若已知函数f(x)的定义域为[a,b],则复合函数f(g(x))的定义域由不等式a≤g(x)≤b求出;(2)若已知函数f(g(x))的定义域为[a,b],则f(x)的定义域为g(x)在[a,b]上的值域.易错警示(1)函数f(g(x))的定义域指的是x的取值范围,而不是g(x)的取值范围;(2)求函数的定义域时,先不要对函数解析式化简;(3)求出函数的定义域后,一定要将其写成集合或区间的形式;(4)函数f(x)±g(x)的定义域是函数f(x),g(x)的定义域的交集.
考法2 求函数的解析式
方法技巧 求函数解析式的常用方法(1)待定系数法:若已知函数类型(如一次函数、二次函数等),则可用待定系数法求解,例如,二次函数可设为f(x)=ax2+bx+c(a≠0),其中a,b,c是待定系数,根据对应项系数相同,列出方程组,解出a,b,c即可.(2)换元法:主要用于解决已知复合函数f(g(x))的解析式求解函数f(x)的解析式的问题,先令g(x)=t,解出x,即用含t 的代数式表示x,然后代入f(g(x))中即可求得f(t),从而求得f(x).要注意新元的取值范围.(3)配凑法:配凑法是将函数f(g(x))的解析式配凑成关于g(x)的形式,进而求出函数f(x)的解析式.
考法3 已知定义域(值域)求参数的值或取值范围
示例6 已知函数f(x)=-x2+4x+1,其中x∈[-1,t ] ,函数的值域为[-4,5],则实数t的取值范围是　　　. 解析 函数f(x)=-x2+4x+1=-(x-2)2+5,对称轴方程为x=2,所以f(x)在[-1,2]上单调递增, f(-1)=- 4, f(2)=5,由-x2+4x+1=-4,可得x=-1或x=5,因为x∈[-1,t ]时,f(x)的值域为[- 4,5],所以2≤t≤5,所以实数t的取值范围是[2,5].
方法技巧 已知函数的定义域(值域)求参数的值或取值范围的解题步骤 (1)将问题转化为含参方程或不等式的解集问题; (2)根据方程或不等式的解集情况确定参数的取值或取值范围.
考法4 分段函数的应用
方法技巧 求分段函数的函数值的步骤(1)确定要求值的自变量属于哪一个区间;(2)代入相应的函数解析式求值,直到求出具体值为止.注意 ①自变量的值不确定时,必须分类讨论,分类标准可参照分段函数不同段的端点;②求值时注意函数奇偶性、周期性的应用;③当出现f(f(a))求值形式时,应由内到外逐层求值;④当求最值时,应分别求出每段上的最值,然后比较大小得到最值.
方法技巧 求参数或自变量的值(范围)的解题思路(1)解决此类问题时,先在分段函数的各段上分别求解,然后将求出的值或范围与该段函数的自变量的取值范围求交集,最后取各段结果的并集即可.(2)如果分段函数的图象易得,也可以画出函数图象后结合图象求解.注意 (1)弄清参数或自变量所在区间是解决分段函数有关问题的先决条件;(2)自变量的取值属于哪一段范围,就用哪一段的解析式来解决问题,即“分段归类”.解得值(范围)后一定要检验其是否符合相应段的自变量的取值范围.
高分帮·“双一流”名校冲刺
提能力 ∙ 数学探索数学探索 与函数有关的新定义问题通思想∙ 方法指导思想方法 分类与整合思想在函数中的应用
数学探索 与函数有关的新定义问题
方法技巧 与函数有关的新定义问题的一般形式:由命题者先给出一个新的概念、新的运算法则,或者给出一个抽象函数的性质等,然后按照这种“新定义”去解决相关的问题.解题的关键是:紧扣新定义的函数的含义,学会语言的翻译、新旧知识的转化,便可使问题顺利获解.如本示例,若能把新定义的一阶整点函数转化为函数f (x)的图象恰好经过一个整点,问题便可迎刃而解.
思想方法 分类与整合思想在函数中的应用