2022高三数学（理科）（全国版）一轮复习课件：第2章第3讲 二次函数与幂函数

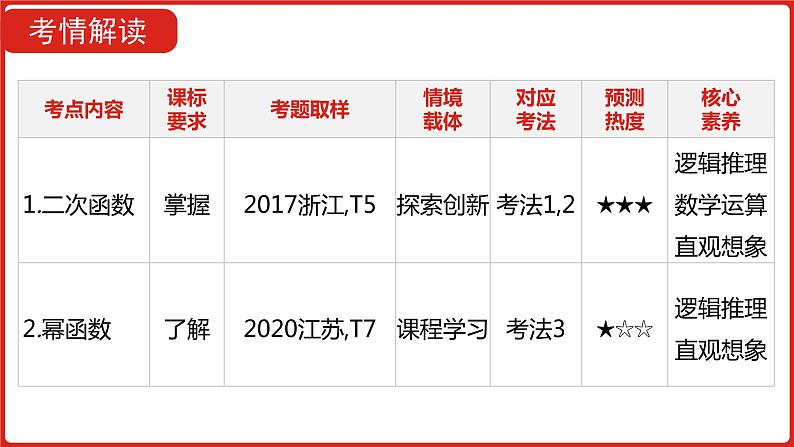
这是一份2022高三数学（理科）（全国版）一轮复习课件：第2章第3讲 二次函数与幂函数，共41页。PPT课件主要包含了提能力∙数学探索，考情解读，考点帮·必备知识通关，二次函数的图象与性质，考法帮·解题能力提升，图2-3-2等内容，欢迎下载使用。

考点帮 · 必备知识通关
考点1 二次函数考点2 幂函数
考法帮 · 解题能力提升
考法1 二次函数的图象及应用
考法2 二次函数的性质及应用
考法3 幂函数的图象与性质的应用
高分帮 ·“双一流”名校冲刺
数学探索 二次函数的零点分布的类型及解题方法
考点1 二次函数考点2 幂函数
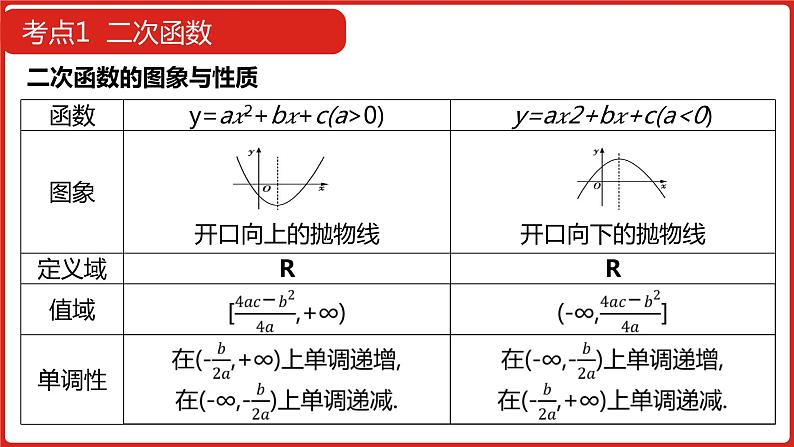
考点1 二次函数
注意 对于函数y=a?2+b?+c,要使它是二次函数,就必须满足a≠0.当题中条件未说明a≠0时,要讨论a=0和a≠0两种情况.
考点2 幂函数
1.幂函数的概念一般地,形如y=?α(α∈R)的函数称为幂函数,其中底数?是自变量,α为常数.2.5个常见幂函数的图象与性质
规律总结 (1)幂函数在(0,+∞)上都有定义,且图象过定点(1,1).(2)当α>0时,幂函数的图象都过点(1,1)和(0,0),且在(0,+∞)上单调递增.当α<0时,幂函数的图象都过点(1,1),且在(0,+∞)上单调递减.(3)幂函数的图象一定会出现在第一象限,一定不会出现在第四象限,若与坐标轴有交点,一定交于原点.(4)幂函数的图象在第一象限的凹凸性:α>1时曲线下凹,0<α<1时曲线上凸,α<0时曲线下凹.(5)在(0,1)上,幂函数的指数越大,函数图象越接近?轴;在(1,+∞)上,幂函数的指数越小,函数图象越接近?轴,注意区分.
考法1 二次函数的图象及应用考法2 二次函数的性质及应用考法3 幂函数图象与性质的应用
考法1 二次函数的图象及应用
示例1 对数函数y=lga?(a>0且a≠1)与二次函数y=(a-1)?2-?在同一坐标系内的图象可能是
方法技巧 识别二次函数图象应学会“三看”
从“三看”入手,能准确判断出二次函数的图象.反之,也能从图象中得到如上信息.
考法2 二次函数的性质及应用
命题角度1　二次函数的最值示例2 已知函数f(?)=-?2+2a?+1-a在0≤?≤1时有最大值2,则实数a的值为　　　　. 思维导引
考法2 二次函数的性质及应用
方法技巧 二次函数在闭区间上最值问题的类型及方法二次函数在闭区间上的最值问题主要有三种类型:①轴定区间定;②轴动区间定;③轴定区间动.不论哪种类型,解题的关键都是讨论对称轴与区间的关系,当含有参数时,要依据对称轴与区间的关系进行分类讨论.二次函数y=a?2+b?+c(a>0)在[m,n]上的最值有如下情况:
命题角度2　与二次函数有关的不等式恒成立问题示例3 [2020河北沧州七校联考]已知两函数f(?)=8?2+16?-k,g(?)=2?2+4?+4,其中k为实数.(1)对任意?∈[-3,3],都有f(?)≤g(?)成立,则k的取值范围为　　　　; (2)存在?∈[-3,3],使f(?)≤g(?)成立,则k的取值范围为　　　　; (3)对任意?1,?2∈[-3,3],都有f(?1)≤g(?2),则k的取值范围为　　　　. 
解析 (1)设h(?)=f(?)-g(?)=6?2+12?-4-k,将原问题转化为?∈[-3,3]时,h(?)≤0恒成立,故h(?)ma?≤0.由二次函数性质可知h(?)ma?=h(3)=86-k,由86-k≤0,得k≥86.(2)由题意知,“存在?∈[-3,3],使f(?)≤g(?)成立”等价于“h(?)=f(?)-g(?)=6?2+12?-4-k≤0在[-3,3]上有解”,故h(?)min≤0.由二次函数的性质可知h(?)min=h(-1)=-10-k,由-10-k≤0,得k≥-10.
(3)对任意?1,?2∈[-3,3],都有f(?1)≤g(?2)成立,所以f(?)ma?≤g(?)min,?∈[-3,3].由二次函数的性质可得f(?)ma?=f(3)=120-k,g(?)min=g(-1)=2.所以120-k≤2,解得k≥118.点评 不等式恒成立问题一般可等价转化为最值问题求解.本题的三小问表面上非常相似,但其本质却大相径庭,应认真审题,深入思考,多加训练,准确掌握不等式成立的充要条件.
考法3 幂函数的图象与性质的应用
示例4 在同一直角坐标系中,函数f(?)=?a(?>0),g(?)=lga?的图象可能是
A　　　　　 B　　　　 C　　　　 D
解析 当a>1时,y=?a与y=lga? 均为增函数,但y=?a 递增越来越快,排除C;当0高分帮·“双一流”名校冲刺
提能力 ∙ 数学探索数学探索 二次函数的零点分布的类型及解题方法
二次函数的零点分布情况多样,比较复杂,常结合二次函数的图象从判别式“Δ”、端点函数值、对称轴三方面入手综合考虑.设二次函数y=f(?)=a?2+b?+c(a>0)对应方程a?2+b?+c=0的根为?1,?2,其零点分布情况如下: 
示例7 m为何值时, f(?)=?2+2m?+3m+4满足下列条件:(1)有且仅有一个零点;(2)有两个零点且均比-1大.思维导引 先将二次函数的零点满足的条件用准确的式子表示出来,然后求解即可.