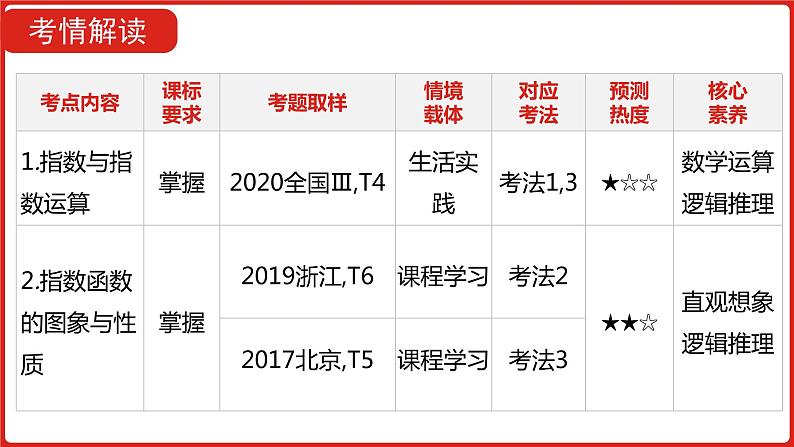
2022高三数学（理科）（全国版）一轮复习课件：第2章第4讲 指数与指数函数

这是一份2022高三数学（理科）（全国版）一轮复习课件：第2章第4讲 指数与指数函数，共34页。PPT课件主要包含了明易错∙误区警示，考情解读，考点帮·必备知识通关，考法帮·解题能力提升，思维导引等内容，欢迎下载使用。

考点帮 · 必备知识通关
考点1 指数与指数运算考点2 指数函数的图象与性质
考法帮 · 解题能力提升
考法1 指数幂的运算
考法2 指数函数的图象及应用
考法3 指数函数的性质及应用
高分帮 ·“双一流”名校冲刺
易错 忽略对底数?的分类讨论而出错
考点1 指数与指数运算
考点2 指数函数的图象与性质
1.指数函数的概念函数y=??(?>0且?≠1)叫作指数函数,其中指数?是自变量,函数的定义域是R,?是底数.辨析比较 幂函数与指数函数的区别
2.指数函数的图象和性质
规律总结 (1)任意两个指数函数的图象都是相交的,过定点(0,1),底数互为倒数的两个指数函数的图象关于y轴对称.(2)当?>1时,指数函数的图象呈上升趋势;当0考法1 指数幂的运算考法2 指数函数的图象及应用考法3 指数函数的性质及应用
考法1 指数幂的运算
方法技巧 指数幂的运算技巧
考法2 指数函数的图象及应用
示例2 (1)已知函数y=k?+?的图象如图2-4-2所示,则函数y =??+k的图象可能是
(2)若曲线|y|=2?+1与直线y=?没有公共点,则?的取值范围是　　　　. 
解析 (1)由函数y=k?+?的图象可得k<0,0-1,所以-1方法技巧 与指数函数有关的图象问题的求解方法
注意 当底数?与1的大小关系不确定时应分类讨论.
考法3 指数函数的性质及应用
考法3 指数函数的性质及应用
方法技巧 比较指数幂大小的常用方法
1.与指数函数有关的复合函数的定义域、值域(1)y=?f(?)的定义域就是f(?)的定义域.(2)求y=?f(?)和y=f(??)的值域的解法.①求形如y=?f(?)的函数的值域,要先令u=f(?),求出u=f(?)的值域,再结合y=?u的单调性求出y=?f(?)的值域.若?的值不确定,则需要对?进行分类讨论:当01时,y=?u为增函数.②求形如y=f(??)的函数的值域,要先求出u=??的值域,再结合y=f(u)的单调性确定y=f(??)的值域.
2.与指数函数有关的复合函数的单调性形如y=?f(?)的函数的单调性,它的单调区间与 f(?)的单调区间有关:若?>1,则函数f(?)的单调增(减)区间即函数y =?f(?)的单调增(减)区间;若0高分帮·“双一流”名校冲刺
明易错∙ 误区警示易错 忽略对底数?的分类讨论而出错
示例6 已知函数y=?2?+2??-1(?>0,且?≠1),当?≥0时,则函数的值域为　　　　. 错因分析 易忽略对底数?的分类讨论而出错.(1)当?>1时,如果?≥0,那么??≥1;(2)当01时,∵?≥0,∴t≥1,∴当?>1时,y≥2.当01时,函数的值域是[2,+∞);当0

相关课件

2022高三数学（理科）（全国版）一轮复习课件：第10章第4讲 圆锥曲线的综合问题：

这是一份2022高三数学（理科）（全国版）一轮复习课件：第10章第4讲 圆锥曲线的综合问题，共60页。PPT课件主要包含了考点帮·必备知识通关，考法帮·解题能力提升，提能力∙数学探索，考情解读，思维导引1，素养探源等内容，欢迎下载使用。

2022高三数学（理科）（全国版）一轮复习课件：第6章第4讲 数列求和及数列的综合应用：

这是一份2022高三数学（理科）（全国版）一轮复习课件：第6章第4讲 数列求和及数列的综合应用，共55页。PPT课件主要包含了考法帮·解题能力提升，提素养∙数学文化，提能力∙数学探索，考情解读，素养探源等内容，欢迎下载使用。

2022高三数学（理科）（全国版）一轮复习课件：第1章第1讲 集合：

这是一份2022高三数学（理科）（全国版）一轮复习课件：第1章第1讲 集合，共34页。PPT课件主要包含了考点帮·必备知识通关，考法帮·解题能力提升，提能力∙数学探索，考情解读，思维导引等内容，欢迎下载使用。