


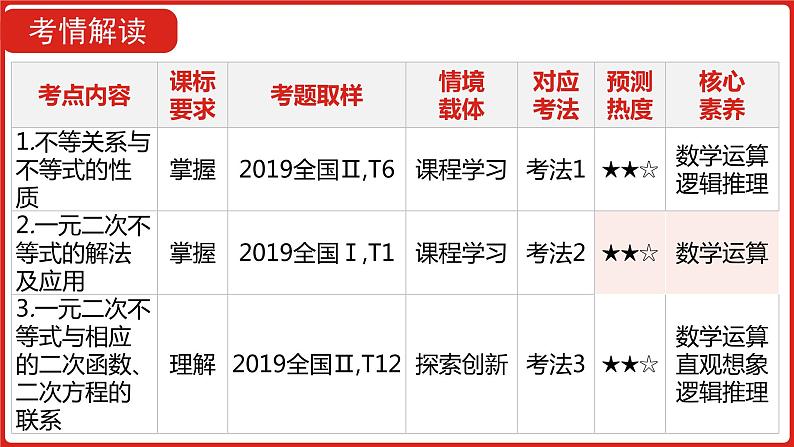




2022高三数学(理科)(全国版)一轮复习课件:第7章第1讲 不等关系与一元二次不等式
展开考点2 一元二次不等式的解法
考法1 不等式性质的应用
考法2 一元二次不等式的解法及其应用
考法3 一元二次不等式的恒成立问题
考点1 不等关系考点2 一元二次不等式的解法
考点1 不等关系
1.两个实数比较大小的方法
考点2 一元二次不等式的解法
1.求一元二次不等式解集的步骤
2.三个“二次”间的关系
对于a<0的情况可同理得出相应的结论.
考法1 不等式性质的应用考法2 一元二次不等式的解法及其应用考法3 一元二次不等式的恒成立问题
考法1 不等式性质的应用
示例1 [2019全国卷Ⅱ,6,5分][理]若a>b,则A.ln(a-b)>0B.3a<3b C.a3-b3>0D.|a|>|b|
命题角度1 判断不等式是否成立
思维导引 由已知选项,取特殊值验证或结合函数的单调性求解.
解析 解法一 由函数y=ln x的图象(图略)知,当0
方法技巧 (1)判断不等式是否成立,需要逐一给出推理判断或反例说明.(2)在判断一个关于不等式的命题的真假时,可结合不等式的性质,对数函数、指数函数的性质进行判断.
命题角度2 求代数式的取值范围
示例2 已知二次函数y=f(x)的图象过原点,且1≤f(-1)≤2,3≤f(1)≤4,则f(-2)的取值范围为 .
用f(1),f(-1)表示f(-2)
得f(-2)的取值范围
方法技巧 利用不等式的性质求取值范围的方法由a
示例3 求下列不等式的解集:(1)-x2+8x-3>0;(2)ax2-(a+1)x+1<0.
命题角度1 一元二次不等式的解法
方法技巧 一元二次型不等式的解法(1)对于常系数一元二次不等式,其求解步骤详见《高考帮》P143求一元二次不等式解集的步骤.(2)解含参数的一元二次型不等式的步骤:①若二次项系数含有参数,则需要对参数进行讨论.当参数等于0时,转化为一次不等式;当参数小于0时,转化为二次项系数为正的形式;当参数大于0时,直接求解.②判断一元二次不等式对应方程根的个数时,常需讨论判别式Δ与0的关系.③确定无根或只有一个根时可直接写出解集;确定方程有两个根时,要讨论两根的大小关系,从而确定不等式的解集.
命题角度2 三个“二次”间的关系
特别提醒 (1)三个二次的关系体现了数形结合,以及函数与方程思想,应用广泛,是高考的热点之一.(2)不等式解集的端点值是相应等价方程的根.
考法3 一元二次不等式的恒成立问题
命题角度1 在R上恒成立
示例5 [2020四川绵阳三诊]若关于x的不等式(a-2)x2+2(a-2)x-4<0对一切实数x恒成立,则实数a的取值范围是A.(-2,2) B.(-∞,-2)∪(2,+∞) C.(-2,2] D.(-∞,2]
思维导引 关于x的不等式的二次项系数含有参数,需要先分a-2=0和a-2≠0两种情况讨论,然后结合已知条件求解即可.
解析 当a-2=0,即a=2时,不等式恒成立,符合题意.当a-2≠0,即a≠2时,要使不等式恒成立,需满足
方法技巧 一元二次不等式在R上恒成立的条件
命题角度2 在给定区间上恒成立
示例6 [2020江西南昌模拟]若对任意的t∈[1,2],函数f(x)=t2x2-(t+1)x+a总有零点,则实数a的取值范围是 .
思维导引 将函数f(x)在t∈[1,2]时总有零点转化为方程f(x)=0在t∈[1,2]时总有解,借助根的判别式,通过分离参数,构造函数g(t),利用函数的性质求得函数g(t)的最值,进而求得结果.
方法技巧 求解不等式恒成立问题的常用方法方法1 不等式解集法不等式f(x)≥0在集合A中恒成立等价于集合A是不等式f(x)≥0的解集B的子集,通过求不等式的解集,并研究集合间的关系可以求出参数的取值范围.方法2 分离参数法若不等式f(x,λ)≥0(x∈D,λ为实参数)恒成立,将f(x,λ)≥0转化为λ≥g(x)或λ≤g(x)(x∈D)恒成立,进而转化为λ≥g(x)max或λ≤g(x)min,求g(x)(x∈D)的最值即可.该方法适用于参数与变量能分离,函数最值易求的题目.
2022高三数学(理科)(全国版)一轮复习课件:第2章第1讲 函数及其表示: 这是一份2022高三数学(理科)(全国版)一轮复习课件:第2章第1讲 函数及其表示,共39页。PPT课件主要包含了考点帮·必备知识通关,考点2分段函数,考法帮·解题能力提升,提能力∙数学探索,考情解读,函数的概念,函数的表示法,思维导引等内容,欢迎下载使用。
2022高三数学(理科)(全国版)一轮复习课件:第1章第2讲 常用逻辑用语: 这是一份2022高三数学(理科)(全国版)一轮复习课件:第1章第2讲 常用逻辑用语,共45页。PPT课件主要包含了考点帮·必备知识通关,考法帮·解题能力提升,提能力∙数学探索,考情解读,定义法,思维导引等内容,欢迎下载使用。
2022高三数学(理科)(全国版)一轮复习课件:第1章第1讲 集合: 这是一份2022高三数学(理科)(全国版)一轮复习课件:第1章第1讲 集合,共34页。PPT课件主要包含了考点帮·必备知识通关,考法帮·解题能力提升,提能力∙数学探索,考情解读,思维导引等内容,欢迎下载使用。












