华师大版九年级下册27.1 圆的认识综合与测试课文内容ppt课件

这是一份华师大版九年级下册27.1 圆的认识综合与测试课文内容ppt课件，共18页。PPT课件主要包含了多边形与圆的位置关系，在学中做在做中学，圆的内接多边形，归纳总结领悟精髓，仔细观察领悟实质，圆的内接四边形，∠A∠DCE，几何语言，学以致用，经典数学等内容，欢迎下载使用。
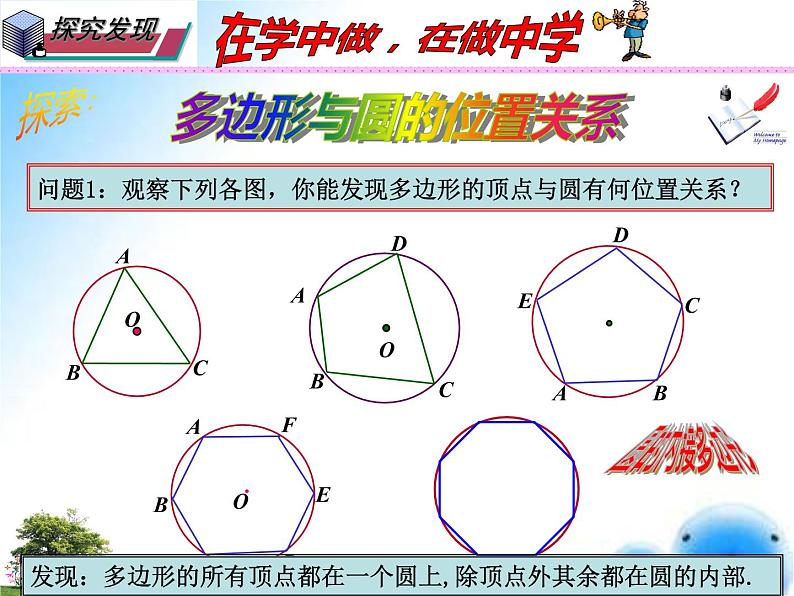
问题1：观察下列各图，你能发现多边形的顶点与圆有何位置关系？
发现：多边形的所有顶点都在一个圆上,除顶点外其余都在圆的内部.
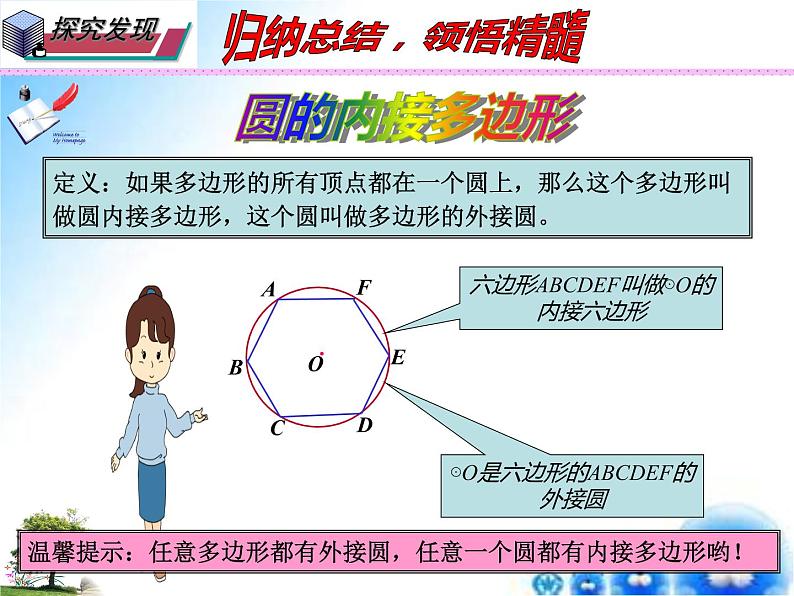
定义：如果多边形的所有顶点都在一个圆上，那么这个多边形叫做圆内接多边形，这个圆叫做多边形的外接圆。
六边形ABCDEF叫做⊙O的内接六边形
⊙O是六边形的ABCDEF的外接圆
温馨提示：任意多边形都有外接圆，任意一个圆都有内接多边形哟！
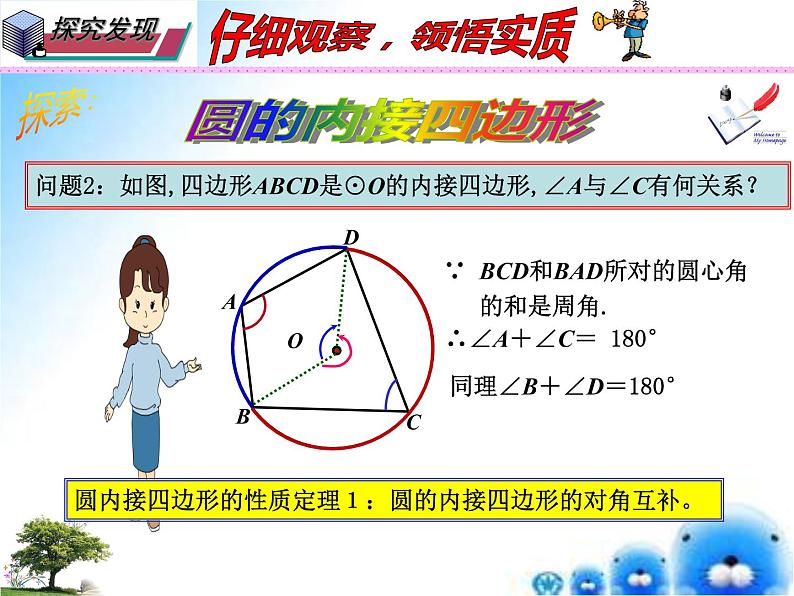
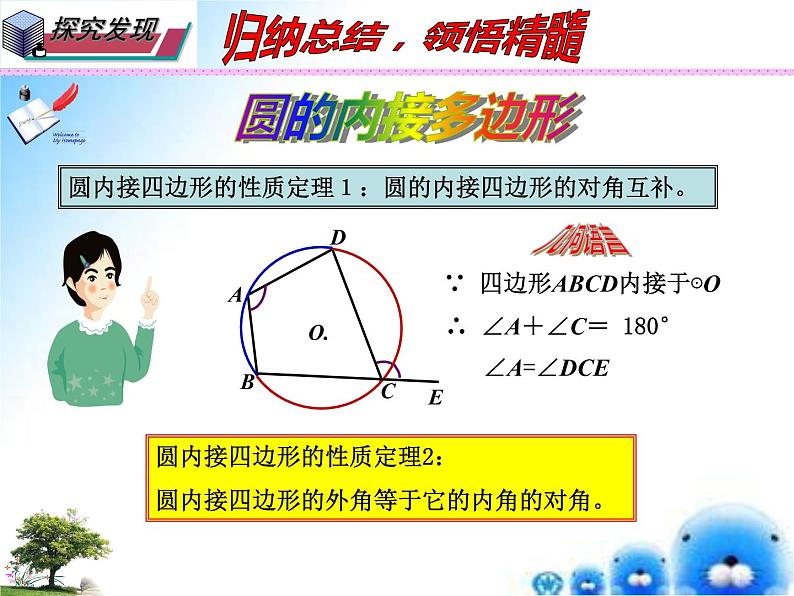
问题2：如图,四边形ABCD是⊙O的内接四边形,∠A与∠C有何关系？
∵ BCD和BAD所对的圆心角 的和是周角.
∴∠A＋∠C＝ 180°
同理∠B＋∠D＝180°
圆内接四边形的性质定理１：圆的内接四边形的对角互补。
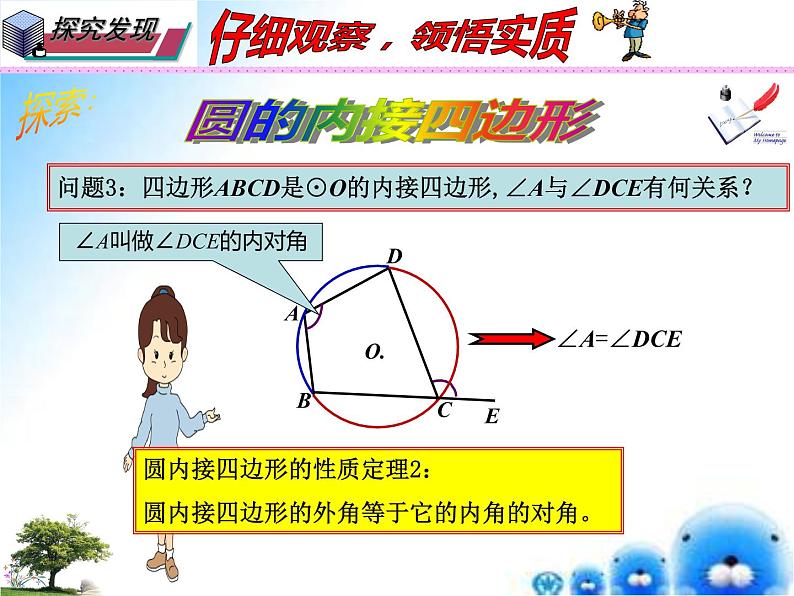
问题3：四边形ABCD是⊙O的内接四边形,∠A与∠DCE有何关系？
∠A叫做∠DCE的内对角
圆内接四边形的性质定理2：圆内接四边形的外角等于它的内角的对角。
∵ 四边形ABCD内接于⊙O
∴ ∠A＋∠C＝ 180°
如图，四边形ABCD是⊙O内接四边形。
（1）若∠BCD=110°，求∠BAD的度数；
（2）若∠A、∠B、∠C的度数之比为2:3:6，求四边形各内角度数。
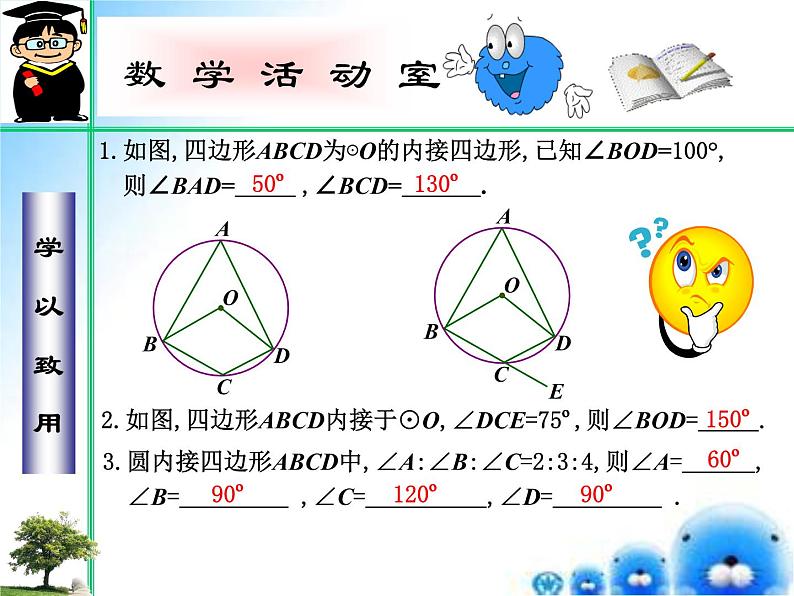
1.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°, 则∠BAD= ,∠BCD= .
2.如图,四边形ABCD内接于⊙O,∠DCE=75º,则∠BOD= .
3.圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4,则∠A= , ∠B= ,∠C= ,∠D= .
4.如图，四边形ABCD是⊙O的内接四边形。
（1）若∠AOC=130°，求∠B的度数；
（2）若∠B=120°，求∠AOC的度数。
如图⊙O1与⊙O2都经过A、B两点.经过点A的直线CD与⊙O1交于点
C,与⊙O2交于点D.经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F.求证：CE∥DF.
变式1：如图，⊙O1和⊙O2都经过A、B两点．过A点的直线CD与⊙O1交于点C，与⊙O2交于点D．过B点的直线EF与⊙O1交于点E，与⊙O2交于点F．求证：CE//DF.
变式2：如图，⊙O1和⊙O2都经过A、B两点．过A点的直线CD与⊙O1交于点C，与⊙O2交于点D．过B点的直线EF与⊙O1交于点E，与⊙O2交于点F，CD//EF.求证：CE=DF
如图,已知四边形ABCD是圆的内接四边形且ABCD是平行四边形。
求证：四边形ABCD是矩形
【拓展】四边形ABCD是圆的内接四边形且ABCD是梯形。 求证：四边形ABCD是等腰梯形。
如图，四边形ABCD是⊙O的内接四边形，BC的延长线于AD的延
长线交于点E，且DC=DE.
（1）求证：∠A=∠AEB；
（2）连结OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形。
1.如图，四边形ABCD是⊙O的内接四边形，AB的延长线于DC的 延长线交于点E，且∠D=∠E.
（1）求证：∠ADC=∠CBE；
（2）求证：CB=CE；
（3）设AD不是⊙O的直径，AD的中点为M，且MB=MC，证明： △ADE为等边三角形
一个人一天也不能没有理想，凭侥幸、怕吃苦、没有真才实学，再好的理想也不能实现不了。