初中数学华师大版七年级上册第5章 相交线与平行线综合与测试教学课件ppt

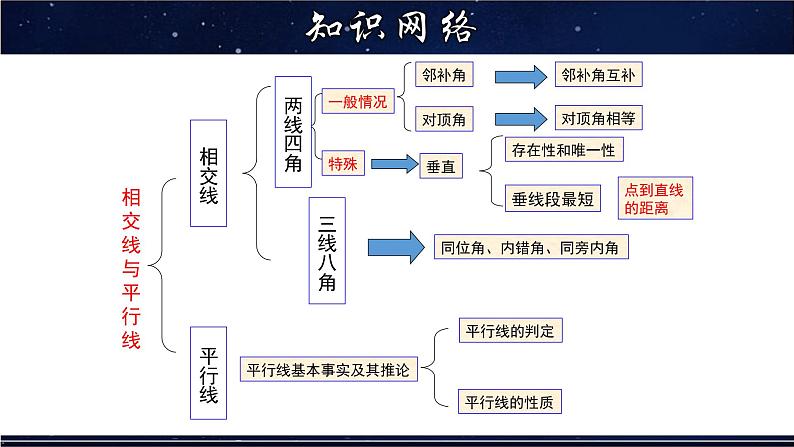
这是一份初中数学华师大版七年级上册第5章 相交线与平行线综合与测试教学课件ppt，共25页。PPT课件主要包含了知识网络，相交线，平行线，相交线与平行线，三线八角，知识梳理，垂线的性质2，平行线的定义，考点解析，相交线相关求角度问题等内容，欢迎下载使用。
同位角、内错角、同旁内角
平行线基本事实及其推论
垂线的性质1：过一点有且只有一条直线与已知直线垂直。
垂直：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直；其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足。
连接直线外一点与直线上各点的所有线段中，垂线段最短。简单说成：垂线段最短。
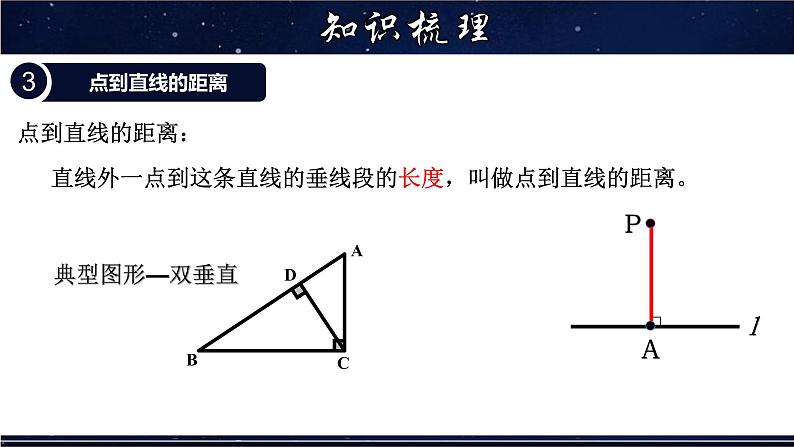
直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。
在同一平面内，不相交的两条直线叫做平行线。
※在同一平面内的两条直线的位置关系有相交或平行两种。
※平行线的基本事实：经过直线外一点，有且只有一条直线与这条直线平行。
※平行线的基本事实的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。
判定方法1两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行。
简单说成：同位角相等，两直线平行。
判定方法2两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行。
简单说成：内错角相等，两直线平行。
简单说成：同旁内角互补，两直线平行。
判定方法3两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行。
性质1两直线平行，同位角相等.
性质2两直线平行，内错角相等.
性质3两直线平行，同旁内角互补.
【例1】如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
∵AB⊥CD，∴∠AOC=90°∵∠AOE=65°∴∠COE=25°又∵∠COE=∠DOF(对顶角相等）∴∠DOF=25°
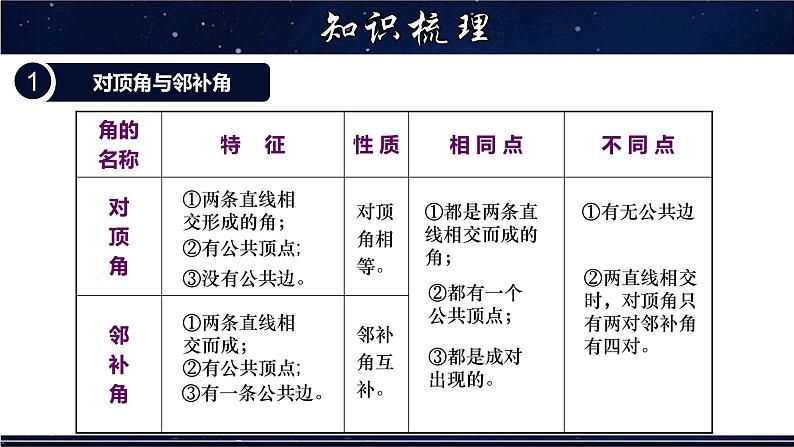
【点睛】两条直线相交包括垂直和斜交两种情形.相交时形成了两对对顶角和四对邻补角.其中垂直是相交的特殊情况，它将一个周角分成了四个直角.
【迁移应用】如图,AB,CD相交于点O,∠AOC=70°,EF平分∠COB,求∠COE的度数.
【例2】如图，AD为三角形ABC的高，能表示点到直线（线段）的距离的线段有（ ）A.2条 B.3条 C.4条 D.5条
【点睛】直线外一点到这条直线的垂线段的长度，叫做点到直线的距离.寻找技巧：1.确定垂线段；2.垂足所在直线为“这条直线”；3.另一端点即是“直线外一点”.
【迁移应用】如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是___cm.
【例3】(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
解：∵∠1=∠2=72°∴a//b (内错角相等，两直线平行）∴∠3+∠4=180° (两直线平行，同旁内角互补)∵∠3=60°∴∠4=120°
证明: ∵∠DAC= ∠ACB (已知)∴ AD//BC(内错角相等,两直线平行)∵ ∠D+∠DFE=180°(已知)∴ AD// EF(同旁内角互补,两直线平行)∴ EF// BC(平行于同一条直线的两条直线互相平行)
(2)已知∠DAC=∠ACB,∠D+∠DFE=180°,求证:EF//BC.
【点睛】平行线的性质和判定经常结合使用，由角之间的关系得出直线平行，进而再得出其他角之间的关系，或是由直线平行得到角之间的关系，进而再由角的关系得出其他直线平行.
【迁移应用】如图：BD平分∠ABC，F在AB上，G在AC上，FC与BD相交于点H.∠GFH+∠BHC=180°，求证：∠1=∠2.
解：∵∠BHC=∠FHD，∠GFH+∠BHC=180°（已知）∴∠GFH+∠FHD=180°（等量代换)∴FG∥ BD（同旁内角互补，两直线平行）∴∠1=∠ABD（两直线平行，同位角相等）∵BD平分∠ABC（已知）∴∠2=∠ABD（角平分线的定义）∴∠1=∠2（等量代换)
解：设∠1的度数为x°,则∠2的度数为x°,∠3的度数为8x°,根据题意可得x°+x°+8x°=180°，解得x=18.即∠1=∠2=18°，而∠4=∠1+∠2（对顶角相等）.故∠4=36°.
【点睛】当题干中出现“角之间的倍数关系或是比值”通常利用方程解决问题。这是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便.在有关线段或角的求值问题中它的应用非常广泛.
【迁移应用】如图，直线AB，CD相交于点0，已知∠AOC＝70°，OE把∠BOD分成两个角，且∠BOE:∠DOE＝2:3，求∠DOE的度数..
解：∵∠AOC=70°∴∠BOD=∠AOC=70°∵∠BOE：∠EOD=2：3设∠BOE=2x，∠EOD=3x∴ 2x+3x= 70°∴x=14°∴∠DOE= 3x=42°
【例5】如图，直线l1∥ l2，∠α=∠β，∠1=40°，则∠2=______.
解：延长CD交直线l2于点E∵l1∥ l2 ∴∠3=∠1=40°∵∠α=∠β∴AB∥ CD∴∠2+∠3=180°∴∠2=180°-∠3=180°-40°=140°
【迁移应用】如图，AB∥ CD，试说明∠B、∠D 、∠BED之间的大小关系.
解：∠B+∠BED=∠D。理由：过点E作EF∥ AB∵AB∥ CD， EF∥ AB （已知）∴AB∥ CD∥ EF（平面内两条直线都与同一条直线平行，这两条直线互相平行）∴∠B=∠BEF，∠D=∠DEF（两直线平行，内错角相等）∵∠BEF+ ∠BED =∠DEF∴ ∠B+∠BED=∠D
若AB∥CD, 则∠ =∠ .
1.如图, 若∠3=∠4，则 ∥ ；
2.如图，∠D=70°，∠C= 110°,∠1=69°，则∠B=_____.
3.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °
4.如图2,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D=( ) A.75° B.45° C.30° D.15°
5.如图，直线AB、CD、EF相交于点O，OG平分∠COF，∠1=30°，∠2=45°,求∠3的度数．
6.如图，A、B、C和D、E、F分别在同一直线上，∠1=∠2，∠C=∠F，求证：∠A=∠D．
证明：∵∠1=∠2，∠2=∠3∴∠1=∠3∴BF∥CE（同位角相等，两直线平行∴∠4=∠C（两直线平行，同位角相等）∵∠C=∠F∴∠4=∠F∴DF∥AC（内错角相等，两直线平行）∴∠A=∠D（两直线平行，内错角相等）