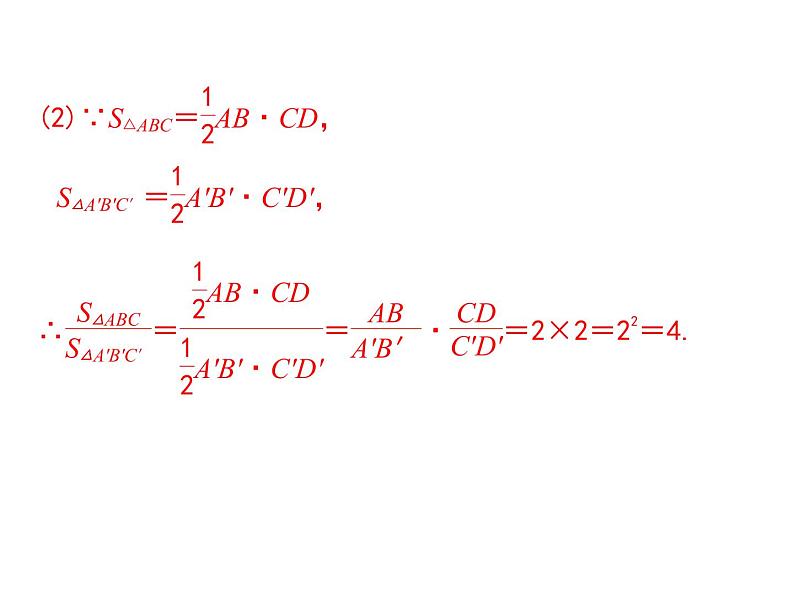
北师大版九年级上册第四章 图形的相似7 相似三角形的性质课前预习课件ppt

这是一份北师大版九年级上册第四章 图形的相似7 相似三角形的性质课前预习课件ppt，共20页。PPT课件主要包含了ADE，ABC，一自主探究，相似比，成比例，对应高的比，对应角平分线的比，对应中线的比，相似比的平方，二合作探究等内容，欢迎下载使用。

1．理解并初步掌握相似三角形的周长比，面积比与相似比的关系．2．会运用相似三角形的性质解决简单的实际问题．
1．顺次连接三角形三边的中点，所成的三角形与原三角形对应边上的中线的比是(　　)
A．1∶2　　　　　 B．2∶1　　　　　C．1∶4　　　　　 D．4∶1
2．如图，DE∥BC，则△______∽△ ______ ．若AD＝3，BD＝2，AF⊥BC，交DE于G，则AG∶AF＝ ______ ，△AGE∽△AFC，且它们的相似比为______
3．已知△ABC与△DEF相似且对应角平分线之比为2∶3，若△ABC的最长边为6，则△DEF的最长边为____ ．
知识模块一　探索相似三角形对应线段的比
1．相似三角形的对应角_______，对应边______；2．相似三角形的___________、________________与_______________都等于相似比；3．相似三角形的周长之比等于______；相似多边形的面积之比等于____________．
问题1：如果△ABC∽△A′B′C′，相似比为2，那么△ABC与△A′B′C′的周长比是多少？面积比呢？
解：(1)∵△ABC∽△A′B′C′，
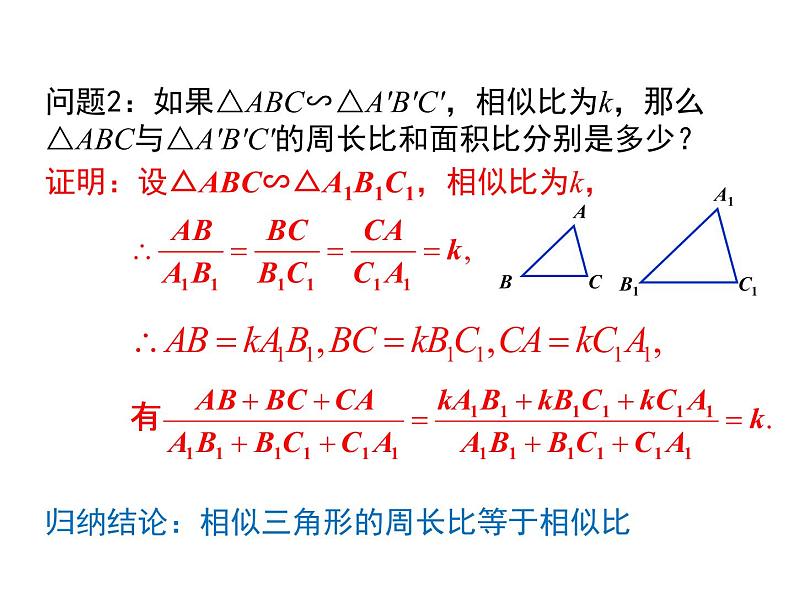
问题2：如果△ABC∽△A′B′C′，相似比为k，那么△ABC与△A′B′C′的周长比和面积比分别是多少？
证明：设△ABC∽△A1B1C1，相似比为k，
归纳结论：相似三角形的周长比等于相似比
证明：设△ABC∽△A′B′C′，相似比为k,
如图，分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形，并且∠B=∠B′，
∴△ABD∽△A′B′D′.
∵△ABC∽△A′B′C′.
归纳结论：相似三角形面积比等于相似比的平方．
议一议：两个相似四边形的周长比等于相似比吗？面积比等于相似比的平方吗？两个相似五边形的周长比与面积比怎样呢？两个相似的n边形呢？
无论是三角形、四边形、还是多边形，都有相同的结论，所以可以推导出：相似多边形的周长比等于相似比，面积比等于相似比的平方．
知识模块二　相似三角形性质的应用
1．若△ABC∽△A′B′C′，相似比为1∶2，则△ABC与△A′B′C′的面积的比为(　 　)
A．1∶2　　　　　B．2∶1　　　　　C．1∶4　　　　　D．4∶1
将△ABC沿BC方向平移得到△DEF，△ABC与△DEF重叠部分的面积是△ABC的面积的一半.已知BC=2，求△ABC平移的距离. 　
解：根据题意，可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC
即，△ABC平移的距离为
1．教材P110页习题4.12的第1题．答：相似，周长比为2∶1，面积比为4∶1.
2．教材P111页习题4.12的第2题．解：(1)∵AB＝2DE，AC＝2DF，∠BAC＝∠EDF.∴△ABC∽△DEF，相似比为2∶1，∴中线AG与DH的比是2∶1；(2)△ABC与△DEF的面积比是4∶1.
1．下列命题中错误的是(　　)A．相似三角形的周长比等于对应中线的比B．相似三角形对应高的比等于相似比C．相似三角形的面积比等于相似比D．相似三角形对应角平分线的比等于相似比
2.把一个五边形改成和它相似的五边形，如果面积扩大到原来的49倍，那么对应的对角线扩大到原来的（ ）A．49倍 B．7倍 C．50倍 D．8倍
3.两个相似多边形的一组对应边分别为3cm和4.5cm，如果它们的面积和为78cm2，那么较大多边形的面积为（ ）A．46.8 cm2 B．42 cm2 C．52 cm2 D．54 cm2
4．若两个相似多边形的面积之比为1∶4，则它们的周长之比为(　　)
A．1∶4　　　B．1∶2　　　C．2∶1　　　D．4∶1
5．若两个三角形相似，且它们的最大边分别为6cm和8cm，它们的周长之和为35cm，则较小的三角形的周长为______．
6.两个相似三角形面积之比为2：7，较大三角形一边上的高为 ，则较小三角形的对应边上的高为_______.
7.两个相似多边形最长的的边分为10cm和25cm，它们的周长之差为60cm，则这两个多边形的周长分别为_____________.
8．在▱ABCD中，BE＝2AE，若S△AEF＝6，求SCDF.
解：∵四边形ABCD是平行四边形，∴DC＝AB，DC∥AB，∴∠DCA＝∠BAC，又∵∠CFD＝∠AFE，∴△AFE∽△CFD，
∴S△CDF＝9S△AEF＝9×6＝54.
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方