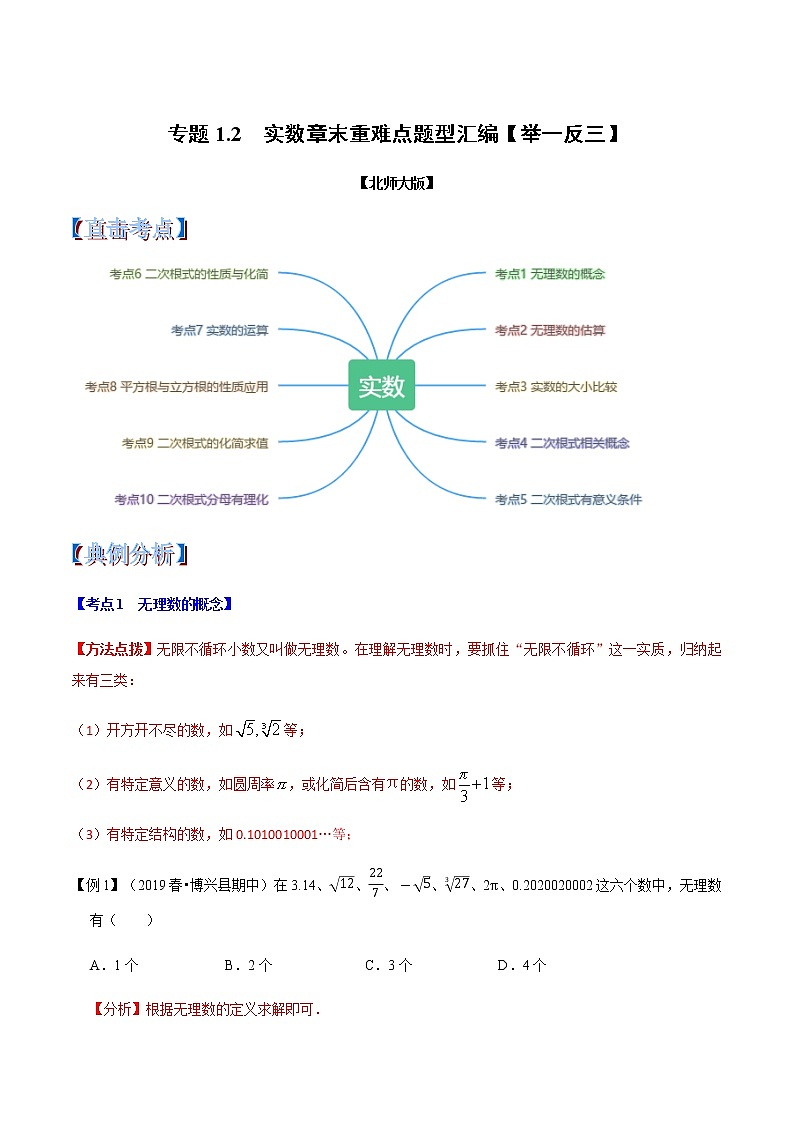


专题1.2 实数章末重难点题型(举一反三)(北师大版)(解析版)学案
展开【考点1 无理数的概念】
【方法点拨】无限不循环小数又叫做无理数。在理解无理数时,要抓住“无限不循环”这一实质,归纳起来有三类:
(1)开方开不尽的数,如等;
(2)有特定意义的数,如圆周率,或化简后含有π的数,如等;
(3)有特定结构的数,如0.1010010001…等;
【例1】(2019春•博兴县期中)在3.14、12、227、-5、327、2π、0.2020020002这六个数中,无理数有( )
A.1个B.2个C.3个D.4个
【分析】根据无理数的定义求解即可.
【答案】解:3.14、227、327、0.2020020002是有理数,
12、-5、2π是无理数,无理数的个数是3,
故选:C.
【点睛】此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,6,0.8080080008…(每两个8之间依次多1个0)等形式.
【变式1-1】(2018春•新罗区校级期中)下列说法中 ①无限小数都是无理数 ②无理数都是无限小数 ③﹣2是4的平方根 ④带根号的数都是无理数.其中正确的说法有( )
A.3个B.2个C.1个D.0个
【分析】分别根据无理数、有理数的定义即可判定选择项.
【答案】解:①无限不循环小数都是无理数,故①错误;
②无理数都是无限不循环小数,故②正确;
③﹣2是4的平方根,故③正确;
④带根号的数不一定都是无理数,故④错误;
故选:B.
【点睛】此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,0.8080080008…(每两个8之间依次多1个0)等形式.
【变式1-2】(2018秋•东台市期中)下列实数中,12、39、-17、π2、﹣3.14、0.1、3-27、0、0.3232232223…(相邻两个3之间依次增加一个2),无理数的个数是( )
A.2个B.3个C.4个D.5个
【分析】根据无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,找出无理数的个数.
【答案】解:12=23,0.1=1010,3-27=-3,
则无理数有:12、39、π2、0.1、0.3232232223…,共5个.
故选:D.
【点睛】本题考查了无理数,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.
【变式1-3】(2019秋•安宁区校级期中)在下列各数中是无理数的有( )
-(-5)2、36、17、0、﹣π、311、3.1415、15、2.010101…(相邻两个1之间有1个0).
A.1个B.2个C.3个D.4个
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【答案】解:﹣π、311、15是无理数,
故选:C.
【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
【考点2 无理数的估算】
【方法点拨】无理数的估算,关键掌握二次根式的性质,能对根式进行估算.
【例2】(2018春•巫山县期中)估计13+12的值在( )
A.1到2之间B.2到3之间C.3到4之间D.4到5之间
【分析】直接利用13的取值范围进而计算得出答案.
【答案】解:∵3<13<4,
∴4<13+1<5,
∴13+12的值在2到3之间.
故选:B.
【点睛】此题主要考查了估算无理数的大小,正确得出13的取值范是解题关键.
【变式2-1】(2019春•北流市期中)设n为正整数,且n<83<n+1,则n的值为( )
A.6B.7C.8D.9
【分析】首先得出81<83<100,得出83的取值范围,即可得出n的值.
【答案】解:∵81<83<100,
∴9<83<10,
又∵n为正整数,
∴n=9.
故选:D.
【点睛】本题主要考查了无理数的估算,熟练掌握二次根式的性质是解答本题的关键.
【变式2-2】(2019春•嘉陵区期中)已知a,b分别是6-13的整数部分和小数部分,则2a﹣b的值是( )
A.13-2B.2-13C.13D.9-13
【分析】先估算3<13<4,然后分别求出a=2,b=6-13-2=4-13,再求解即可;
【答案】解:∵3<13<4,
∴6-13的整数部分是2,即a=2,
6-13的小数部分是6-13-2=4-13,即b=4-13,
∴2a﹣b=4﹣4+13=13;
故选:C.
【点睛】本题考查无理数的估算;熟练掌握无理数的估算方法是解题的关键.
【变式2-3】(2019春•郯城县期中)若a是10-1的整数部分,b是5+5的小数部分,则a(5-b)的值为( )
A.6B.4C.9D.35
【分析】先估算10和5的大小,然后求出a、b的值,代入所求式子计算即可.
【答案】解:∵2<10-1<3,
∴a=2,
又∵7<5+5<8,
∴5+5的整数部分为7
∴b=5+5-7=5-2;
∴a(5-b)=2×(5-5+2)=4.
故选:B.
【点睛】本题主要考查估算无理数的大小,解题的关键是求出无理数整数部分的值,属于基础题.
【考点3 实数的大小比较】
【方法点拨】实数大小比较常见方法有:倒数法、作差法、作商法、放缩法、两边平方法等等.
【例3】(2019秋•河北期中)已知a=7-5,b=5-3,c=3-7,则a、b、c三个数的大小关系是( )
A.b>c>aB.b>a>cC.a>b>cD.c>a>b
【分析】首先求出a,b,c的倒数,进而比较它们的大小,进而得出a、b、c三个数的大小关系.
【答案】解:∵a=7-5,b=5-3,c=3-7,
∴1a=17-5=7+52,
1b=15-3=5+32,
1c=13-7=3+72,
∵7>3,
∴1a>1b,
∵3>5,
∴1a<1c,
∴1c>1a>1b,
∴b>a>c.
故选:B.
【点睛】此题主要考查了实数比较大小,正确求出a,b,c的倒数大小是解题关键.
【变式3-1】(2019春•洪山区期中)比较实数:2、5、37的大小,正确的是( )
A.37<2<5B.2<37<5C.5<37<2D.2<5<37
【分析】应用放缩法,判断出2、5、37的大小关系即可.
【答案】解:∵2=4<5,
∴2<5,
∵37<38=2,
∴37<2,
∴37<2<5.
故选:A.
【点睛】此题主要考查了实数大小比较的方法,要熟练掌握,注意放缩法的应用.
【变式3-2】(2019春•淮北期中)比较3-1与32的大小,结果是( )
A.前者大B.后者大C.一样大D.无法确定
【分析】首先用3-1减去32,判断出3-1与32的差的正负,然后根据3-1与32的差的正负情况,判断出3-1与32的大小关系即可.
【答案】解:∵3-1-32=32-1<42-1=1﹣1=0,
∴3-1-32<0,
∴3-1<32,
∴比较3-1与32的大小,结果是后者大.
故选:B.
【点睛】此题主要考查了实数大小比较,要熟练掌握,解答此题的关键是判断出3-1与32的差的正负.
【变式3-3】(2019秋•乐山校级期中)已知a=2-1,b=6-2,c=22-6,那么a、b、c的大小关系是( )
A.a<b<cB.c<b<aC..b<a<cD..c<a<b
【分析】利用作差法比较a和b、b和c、a和c的大小,再比较a、b、c三者的大小.
【答案】解:∵a﹣c=2-1﹣(22-6)
=6-(1+2)
≈2.449﹣2.414>0,
∴a>c;
∵a﹣b=2-1﹣(6-2)=2+1-6
≈2.414﹣2.449<0,
∴a<b,
∴c<a<b.
故选:D.
【点睛】此题主要考查了实数的大小的比较,其中比较两个实数的大小,可以采用作差法、取近似值法、比较n次方的方法等.
【考点4 二次根式相关概念】
【方法点拨】(1)二次根式的定义:一般地,形如(a≥0)的式子叫做二次根式。
最简二次根式满足的条件:①被开方数不含分母;②被开方数中不含能开得尽方的因数或因式。
同类二次根式:几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫做同类二次根式。 要判断几个根式是不是同类二次根式,须先化简根号里面的数,把非最简二次根式化成最简二次根式,然后判断。
【例4】(2018春•禹州市期中)下列各式:10,2a,b2-1,x2+y2,-3,4,m2+1中,一定是二次根式的个数是( )
A.3个B.4个C.5个D.7个
【分析】直接利用二次根式的定义分析得出答案.
【答案】解:10,2a,b2-1,x2+y2,-3,4,m2+1中,一定是二次根式的是:
10,x2+y2,4,m2+1共4个.
故选:B.
【点睛】此题主要考查了二次根式的定义,正确把握相关定义是解题关键.
【变式4-1】(2019春•莱芜期中)二次根式:①9-x2;②(a+b)(a-b);③a2-2a+1;④1x;⑤0.75中最简二次根式是( )
A.①②B.③④⑤C.②③D.只有④
【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
【答案】解:③a2-2a+1=(a-1)2=|a﹣1|,被开方数含有开得尽方的因式,不是最简二次根式;
④1x=xx⋅x=xx,被开方数含有分母,不是最简二次根式;
⑤0.75=34=32,被开方数含有小数(分数),不是最简二次根式;
因此只有①②符合最简二次根式的条件.
故选:A.
【点睛】根据最简二次根式的定义,最简二次根式必须满足两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.
被开方数是多项式时,还需将被开方数进行因式分解,然后再观察判断.
【变式4-2】(2019春•泰兴市期中)如果12与最简二次根式7-2a是同类二次根式,那么a的值是( )
A.﹣2B.﹣1C.1D.2
【分析】根据最简二次根式与同类二次根式的定义列方程组求解.
【答案】解:12=23.
由题意,得
7﹣2a=3,解得a=2,
故选:D.
【点睛】此题主要考查了同类二次根式的定义,即:二次根式化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.
【变式4-3】(2019春•定州市期中)与a3b不是同类二次根式的是( )
A.ab2B.baC.1abD.ba3
【分析】根据同类二次根式的意义,将题中的根式化简,找到被开方数相同者即可.
【答案】解:a3b=|a|ab
A、ab2=2ab2与|a|ab被开方数不同,不是同类二次根式;
B、ba=ab|a|与|a|ab被开方数相同,是同类二次根式;
C、1ab=abab与|a|ab被开方数相同,是同类二次根式;
D、ba3=aba2与|a|ab被开方数相同,是同类二次根式.
故选:A.
【点睛】此题主要考查了同类二次根式的定义,即化成最简二次根式后,被开方数相同,这样的二次根式叫做同类二次根式.
【考点5 二次根式有意义条件】
【方法点拨】二次根式有意义条件需满足被开方数大于等于0.
【例5】(2018秋•东营区校级期中)二次根式2-xx+3在实数范围内有意义,则x的取值范围是 .
【分析】直接利用二次根式的定义结合分式的定义分析得出答案.
【答案】解:∵二次根式2-xx+3在实数范围内有意义,
∴2﹣x≥0,且x+3≠0,
解得:x≤2且x≠﹣3.
故答案为:x≤2且x≠﹣3.
【点睛】此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.
【变式5-1】(2019春•杭锦后旗期中)已知y=x-1+1-x+3,则x﹣y= .
【分析】根据二次根式有意义的条件确定出x的值,进而得出y的值,代入即可求解.
【答案】解:∵y=x-1+1-x+3,
∴x-1≥01-x≥0
解得:x=1
∴y=3
∴x﹣y=﹣2
故答案为:﹣2
【点睛】本题考查考查二次根式有意义的条件,解题的关键是熟练运用二次根式的性质,本题属于基础题型.
【变式5-2】(2019春•黄石期中)已知实数a满足|2006﹣a|+a-2007=a,则a﹣20062= .
【分析】根据被开方数大于等于0可以求出a≥2007,然后去掉绝对值号整理,再两边平方整理即可得解.
【答案】解:根据题意得,a﹣2007≥0,
解得a≥2007,
∴原式可化为:a﹣2006+a-2007=a,
即a-2007=2006,
两边平方得,a﹣2007=20062,
∴a﹣20062=2007.
故答案为:2007.
【点睛】本题考查了二次根式有意义的条件,解法巧妙,先求出a的取值范围然后去掉绝对值号是解题的关键,也是本题的突破口.
【变式5-3】(2018春•荔湾区校级期中)已知a=2b2-4+4-b2b-2+3b,则a+b的立方根是 .
【分析】根据二次根式的被开方数是非负数求得b=﹣2,继而求得a的值,代入求值即可.
【答案】解:由题意,得b2=4且b﹣2≠0.
所以b=﹣2,
所以a=﹣6.
所以a+b=﹣8.
所以3-8=-2.
故答案是:﹣2.
【点睛】考查了二次根式的意义和性质.概念:式子a(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.
【考点6 二次根式的性质与化简】
【方法点拨】掌握二次根式的性质是关键:① (a≥0); ② (a≥0); ③ (a
取全体实数)。
【例6】(2019春•昌江区校级期中)把根号外的因式移到根号内:(a-1)11-a= .
【分析】根据条件可以得到1﹣a>0,原式可以化成=﹣(1﹣a)11-a,然后根据二次根式的乘法法则即可求解.
【答案】解:原式=﹣(1﹣a)11-a=-(1-a)2•11-a=-(1-a)2⋅11-a=-1-a.
故答案是:-1-a.
【点睛】本题考查了二次根式的化简,正确理解题目中的隐含条件:1﹣a>0是关键.
【变式6-1】(2018春•宜兴市期中)已知xy>0,则化简代数式x-yx2的结果是 .
【分析】首先判断出x,y的符号,再利用二次根式的性质化简求出答案.
【答案】解:∵xy>0,且-yx2有意义,
∴x<0,y<0,
∴x-yx2=x•-y-x=--y.
故答案为:--y.
【点睛】此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键.
【变式6-2】(2018春•肥城市期中)若4x2-4x+1=1﹣2x,则x的取值范围是 .
【分析】已知等式变形后,利用二次根式性质及绝对值的代数意义判断即可求出x的范围.
【答案】解:已知等式变形得:(2x-1)2=|2x﹣1|=1﹣2x,
∴2x﹣1≤0,
解得:x≤12.
故答案为:x≤12.
【点睛】此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.
【变式6-3】(2018秋•杞县期中)实数a、b、c在数轴上的对应点的位置如图,化简:
a2+|a+b|+(c-a)2-|b-c|= .
【分析】根据图可得出c>0>b>a,再去绝对值和根号即可.
【答案】解:由题得,c>0>b>a,
∴a2+|a+b|+(c-a)2-|b-c|
=﹣a﹣a﹣b+c﹣a+b﹣c
=﹣3a.
故答案为﹣3a.
【点睛】本题考查了二次根式的性质化简以及绝对值、数轴,是基础知识要熟练掌握.
【考点7 实数的运算】
【例7】(2019春•老河口市期中)计算:
(1)(-2)2×(-2)2+3(-4)3×(-12)2-327
(2)|2-3|+|1-2|+3(3-13)
【分析】(1)直接利用立方根以及二次根式的性质化简得出答案;
(2)直接利用绝对值的性质以及二次根式的性质计算得出答案.
【答案】解:(1)原式=2×2+(-4)×14-3
=4﹣1﹣3
=0;
(2)原式=3-2+2-1+3-1
=3+1.
【点睛】此题主要考查了实数运算,正确化简各数是解题关键.
【变式7-1】(2019春•费县期中)(1)计算:(1)(-2)2×14+|3-8|+2×(-1)2019
(2)解方程:3(x﹣2)2=27
【分析】(1)直接利用二次根式以及立方根的性质分别化简进而得出答案;
(2)直接利用平方根的性质计算得出答案.
【答案】解:(1)原式=4×12+2+-2
=4-2;
(2)3(x﹣2)2=27
(x﹣2)2=9,
则x﹣2=±3,
解得:x=﹣1或5.
【点睛】此题主要考查了实数运算,正确化简各数是解题关键.
【变式7-2】(2019春•阆中市期中)计算
(1)4-327-|3-8|+318-(-2)2;
(2)3(13-3)-|2-2|.
【分析】(1)直接利用立方根以及算术平方根的定义分别化简得出答案;
(2)直接利用绝对值的性质以及二次根式的乘法运算法则计算得出答案.
【答案】解:(1)原式=2﹣3﹣2+12-2
=﹣412;
(2)原式=1﹣3﹣(2-2)
=﹣4+2.
【点睛】此题主要考查了实数运算,正确化简各数是解题关键.
【变式7-3】(2019春•泰山区期中)计算:
(1)32-20+50-80
(2)313÷116×225
(3)239x+7x2-3x1x-3218x
(4)(2-3)2(5+26).
【分析】(1)先把二次根式化为最简二次根式,然后合并即可;
(2)根据二次根式的乘除法则运算;
(3)先把二次根式化为最简二次根式,然后合并即可;
(4)先利用完全平方公式计算,然后利用平方差公式计算.
【答案】解:(1)原式=42-25+52-45
=92-65;
(2)原式=103×67×125
=4217;
(3)原式=2x+72x2-3x-92x2
=-x-2x;
(4)原式=(2+3﹣26)(5+26)
=25﹣24
=1.
【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.
【考点8 平方根与立方根的性质应用】
【方法点拨】理解平方根、算术平方根、立方根的定义是关键:
(1)一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根。
(2)一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根。
(3)一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根。
【例8】(2019春•中山市期中)已知一个正数m的平方根是2a﹣1与2﹣a,a+b+2立方根是2,求m+b的平方根.
【分析】首先根据:一个正数的平方根是2a﹣1和2﹣a,可得:(2a﹣1)+(2﹣a)=0,据此求出a和m的值;然后根据a+b+2的立方根是2,可得:a+b+2=23=8,据此求出b的值;最后求出m+b的平方根即可.
【答案】解:∵2a﹣1与2﹣a是正数m的平方根
∴(2a﹣1)+(2﹣a)=0,
∴a=﹣1;
∴m=(﹣1)2=1;
∵a+b+2立方根是2,
∴a+b+2=8,
∴b=7;
∴m+b=1+7=8.
所以m+b的平方根是±22.
【点睛】此题主要考查了平方根的性质和应用,以及立方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0.
【变式8-1】(2019春•乐陵市期中)已知一个正数的平方根是2a﹣3和5﹣a,b的立方根是﹣2,求2a﹣b的平方根.
【分析】首先根据:一个正数的平方根是2a﹣3和5﹣a,可得:(2a﹣3)+(5﹣a)=0,据此求出a的值是多少;然后根据:b的立方根是﹣2,可得:b=(﹣2)3=﹣8,据此求出2a﹣b的平方根是多少即可.
【答案】解:∵一个正数的平方根是2a﹣3和5﹣a,
∴(2a﹣3)+(5﹣a)=0,
∴a+2=0,
解得a=﹣2;
∵b的立方根是﹣2,
∴b=(﹣2)3=﹣8,
∴2a﹣b
=2×(﹣2)﹣(﹣8)
=﹣4+8
=4
2a﹣b的平方根是:±4=±2.
【点睛】此题主要考查了平方根的性质和应用,以及立方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0.
【变式8-2】(2018春•孝南区期中)已知正数x的两个不同的平方根分别是2a﹣1和a﹣5,且x﹣y﹣3的立方根为3.
(1)填空:x= ,y= ,a= ;
(2)求x﹣y+3a的平方根.
【分析】(1)根据一个正数的两个平方根互为相反数,可得a的值,再根据平方根的意义,可得x,根据立方根的意义,可得y,
(2)根据平方根的意义,可得答案.
【答案】解:(1)由正数x的两个不同的平方根分别是2a﹣1和a﹣5,得
2a﹣1+a﹣5=0,
解得a=2,
由平方根的意义,得
x=(2a﹣1)2=9;
x﹣y﹣3的立方根为3,
得x﹣y﹣3=33,
解得y=﹣21,
故答案为:9,﹣21,2;
(2)x﹣y+3a=9﹣(﹣21)+3×2=36,
x﹣y+3a的平方根是±36=±6.
【点睛】本题考查了立方根、平方根,利用立方根的意义、平方根的意义是解题关键.
【变式8-3】(2018春•鄂城区期中)已知A=m-4m+3是m+3的算术平方根B=2m-4n+3n-2是n﹣2的立方根,试求:
(1)m和n的值;
(2)A﹣B的值.
【分析】根据算术平方根和立方根的定义得出方程组,求出m、n,再求出A、B,即可得出答案.
【答案】解:(1)∵A=m-4m+3是m+3的算术平方根,B=2m-4n+3n-2是n﹣2的立方根,
∴m﹣4=2,2m﹣4n+3=3,
解得:m=6,n=3,
(2)∵m=6,n=3,
∴A=9=3,B=31=1,
∴A﹣B=3﹣1=2.
【点睛】本题考查了算术平方根和立方根的定义,能根据算术平方根和立方根的定义求出m、n的值是解此题的关键.
【考点9 二次根式的化简求值】
【例9】(2019春•芜湖期中)已知x=12+1,y=12-1,分别求下列代数式的值;
(1)x2+y2;
(2)yx+xy.
【分析】(1)先将x、y进行分母有理化,得到x=2-1,y=2+1,再求出x﹣y与xy的值,然后根据完全平方公式得出x2+y2=(x﹣y)2+2xy,再整体代入即可;
(2)将所求式子变形为x2+y2xy,再整体代入即可.
【答案】解:(1)∵x=12+1=2-1,y=12-1=2+1,
∴x﹣y=﹣2,xy=2﹣1=1,
∴x2+y2=(x﹣y)2+2xy=(﹣2)2+2×1=6;
(2)∵x2+y2=6,xy=1,
∴原式=x2+y2xy=61=6.
【点睛】本题考查二次根式的化简求值,分母有理化,解题的关键是运用完全平方公式以及整体思想,本题属于基础题型.
【变式9-1】(2018秋•通川区校级期中)已知x=13-22,y=13+22,求:(1)x2y﹣xy2的值;(2)x2﹣xy+y2的值.
【分析】先将x和y的值分母有理化后,计算xy和x+y的值,再分别代入(1)和(2)问代入计算即可.
【答案】解:∵x=13-22=3+22(3-22)(3+22)=3+22,y=13+22=3-22(3+22)(3-22)=3﹣22,
∴xy=13-22⋅13+22=1,x+y=3+22+3﹣22=6,
∴(1)x2y﹣xy2,
=xy(x﹣y),
=1×[(3+22)-(3-22)],
=42;
(2)x2﹣xy+y2,
=(x+y)2﹣3xy,
=62﹣3×1,
=36﹣3,
=33.
【点睛】本题主要考查了二次根式的化简求值,在解答时应先化简x和y的值,并利用提公因式法和完全平方公式将所求式子进行变形是关键.
【变式9-2】(2018秋•雁塔区校级期中)已知:x=6+56-5,y=6-56+5.求下列代数式x2﹣3xy+y2的值.
【分析】先将x,y分母有理化,再将其代入到原式=(x﹣y)2﹣xy,计算可得.
【答案】解:x=6+56-5=(6+5)2(6+5)(6-5)=6+2×6×5+56-5=11+230,
y=6-56+5=(6-5)2(6+5)(6-5)=6-2×6×5+56-5=11﹣230,
∴原式=(x﹣y)2﹣xy
=(11+230-11+230)2﹣(11+230)×(11﹣230)
=(430)2﹣(121﹣120)
=480﹣1
=479.
【点睛】本题主要考查二次根式的化简求值,解题的关键是熟练掌握二次根式的混合运算顺序和运算法则.
【变式9-3】(2018春•芜湖期中)已知M=x+yx-y-2xyxy-yx,N=3x-2yx+y+y-x.甲、乙两个同学在y=x-8+8-x+18的条件下分别计算了M和N的值.甲说M的值比N大,乙说N的值比M大.请你判断他们谁的结论是正确的,并说明理由.
【分析】先由题意计算出xy的值,再将xy的值分别代入M、N,求出结果,再进行比较即可.
【答案】解:乙的结论正确.(1分)
理由:由y=x-8+8-x+18,可得x=8,y=18.(3分)
因此M=x+yx-y-2xyx-y=(x-y)2x-y=x-y=8-18=-2.(6分)
N=38-21826+10=62-6226+10=0.(9分)
∴M<N,
即N的值比M大.(10分)
【点睛】本题考查了二次根式的化简求值,解题的关键是根据二次根是有意义的条件,被开方数大于等于0,求得x、y的值.
【考点10 二次根式分母有理化】
【例10】(2019春•瑶海区期中)阅读理解材料:把分母中的根号化掉叫做分母有理化,例如:
①25=255⋅5=255;②12-1=1×(2+1)(2-1)(2+1)=2+1(2)2-12=2+1等运算都是分母有理化.根据上述材料,
(1)化简:13-2
(2)计算:12+1+13+2+14+3+⋯+110+9.
【分析】(1)原式分母有理化,计算即可得到结果;
(2)原式各自分母有理化化简后,合并即可得到结果.
【答案】解:(1)原式=3+2(3-2)(3+2)=3+2;
(2)原式=2-1+3-2+⋯+10-9=10-1.
【点睛】此题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.
【变式10-1】(2019秋•唐河县期中)阅读下列材料,然后回答问题:
在进行二次根式运算时,我们有时会碰上如23、23+1这样的式子,其实我们还可以将其进一步化简:23=2×33×3=233;23+1=2(3-1)(3+1)(3-1)=2(3-1)(3)2-1=3-1.
以上这种化简过程叫做分母有理化.
23+1还可以用以下方法化简:23+1=3-13+1=(3)2-13+1=(3+1)(3-1)3+1=3-1.
请任用其中一种方法化简:①215-3;②523+7.
【分析】①根据平方差公式分母有理化即可求解;
②把分子5变为12﹣7,再根据平方差公式分解因式,再约分计算即可求解.
【答案】解:①215-3
=2(15+3)(15-3)(15+3)
=15+33;
②523+7
=12-723+7
=(23+7)(23-7)23+7
=23-7.
【点睛】本题主要考查了分母有理化,解题的关键是找准有理化因式.
【变式10-2】(2019春•金平区校级期中)观察下列等式:
第一个等式:a1=11+2=2-1
第二个等式:a2=12+3=3-2
第三个等式:a3=13+2=2-3
按上述规律,回答以下问题:
(1)请写出第四个等式:a4= = ;
(2)利用以上规律计算:a1+a2+a3+…+a11;
(3)求(13+5+15+7)(7+3)的值.
【分析】(1)先根据所给的式子找出第一、第二、第三个式子的规律,进而可求出第四个等式;
(2)把所给式子相加,找出规律即可进行计算;
(3)根据所给规律探索可得出原式=12×(7-3)(7+3),再根据平方差公式易得结果.
【答案】解:(1)第四个等式:a4=12+5=5-2;
(2)a1+a2+a3+…+a11;
=2-1+3-2+2-3+⋯+23-11
=23-1;
(3)(13+5+15+7)×(7+3)
=12×(7-3)(7+3)
=12×(7﹣3)
=2.
故答案为:12+5,5-2.
【点睛】考查的是规律型:数字的变化类,是一道找规律的题目,关键是通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题,熟练掌握分数的拆分计算.
【变式10-3】(2019秋•东明县期中)阅读理解:【知识链接】
(1)有理化因式:两个含有根式的代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:2的有理化因式是2;1-x2+2的有理化因式是1+x2+2.
(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去,指的是如果二次根式中分母有根号,那么通常在分子、分母上同乘以一个二次根式,达到化去分母中根号的目的.
【知识运用】
(1)填空:x的有理化因式是 ;a+b的有理化因式是 ;-m-1-m+1的有理化因式是 .
(2)把下列各式的分母有理化:
①1x+y;②6+22-6.
【分析】(1)根据有理化因式定义可知,有理化因式的两个式子是平方差公式或是同一个二次根式;
(2)通过观察,发现:分母有理化的两个步骤:1、同乘分母的有理化因式;2、因式分解达到约分的目的.
【答案】解:(1)x的有理化因式是x;a+b的有理化因式是a-b;-m-1-m+1的有理化因式是-m-1+m+1.
故答案为:x;a-b;-m-1+m+1;
(2)①1x+y=x-y(x+y)(x-y)=x-yx2-y;
②6+22-6=(2+6)2(2-6)(2+6)=2+212+62-6=-8+434=-2-3.
【点睛】本题主要考查了分母有理化,解题的关键是根据材料能正确的进行分母有理化.
苏科版数学八年级上册第4章实数章末重难点题型(举一反三)(原卷+解析卷)学案: 这是一份苏科版数学八年级上册第4章实数章末重难点题型(举一反三)(原卷+解析卷)学案,文件包含苏科版数学八年级上册第4章实数章末重难点题型举一反三解析版docx、苏科版数学八年级上册第4章实数章末重难点题型举一反三原卷版docx等2份学案配套教学资源,其中学案共39页, 欢迎下载使用。
苏科版数学八年级上册第6章一次函数章末重难点题型(举一反三)(原卷+解析卷)学案: 这是一份苏科版数学八年级上册第6章一次函数章末重难点题型(举一反三)(原卷+解析卷)学案,文件包含苏科版数学八年级上册第6章一次函数章末重难点题型举一反三解析版docx、苏科版数学八年级上册第6章一次函数章末重难点题型举一反三原卷版docx等2份学案配套教学资源,其中学案共51页, 欢迎下载使用。
专题1.9 期末考试重难点题型(举一反三)(北师大版)(解析版)学案: 这是一份初中数学北师大版八年级上册本册综合导学案,共62页。学案主要包含了北师大版,变式1-1,变式1-2,变式1-3,变式2-1,变式2-2,变式2-3,变式3-1等内容,欢迎下载使用。













