北师大版九年级下册第三章 圆6 直线与圆的位置关系示范课ppt课件

这是一份北师大版九年级下册第三章 圆6 直线与圆的位置关系示范课ppt课件，共36页。PPT课件主要包含了三角形的“四心”等内容，欢迎下载使用。
2.三角形的外心：定义：
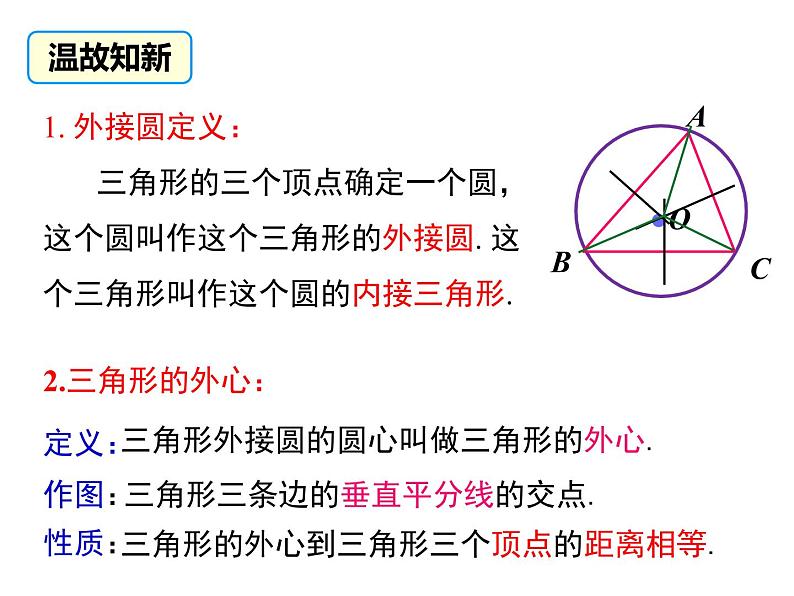
1. 外接圆定义： 三角形的三个顶点确定一个圆，这个圆叫作这个三角形的外接圆. 这个三角形叫作这个圆的内接三角形.
三角形的外心到三角形三个顶点的距离相等.
三角形外接圆的圆心叫做三角形的外心.
三角形三条边的垂直平分线的交点.
重点：切线的判定定理,三角形的内切圆. 难点：熟练运用切线的性质和判定解决有关的证明和计算，学会添加辅助线.
1.理解并掌握圆的切线的判定定理及运用.2.三角形的内切圆和内心的概念及性质.
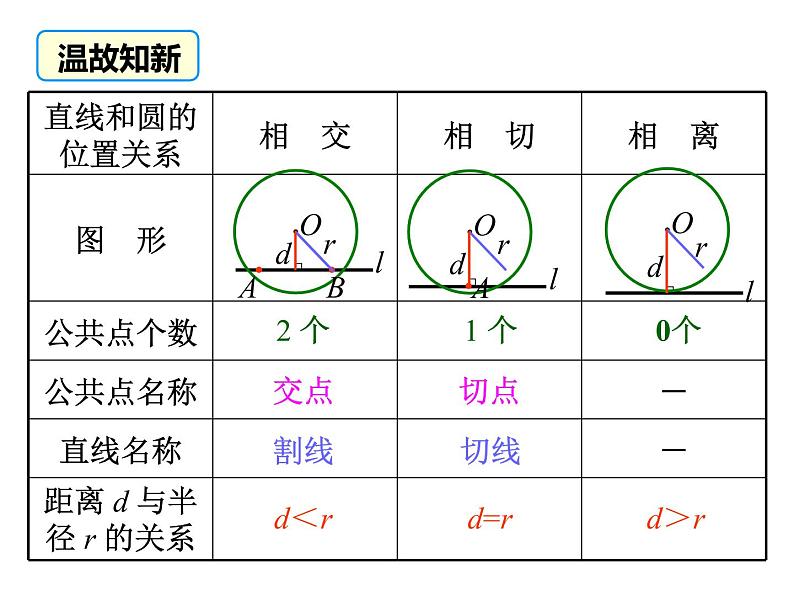
下图中让你感受到了直线与圆的哪种位置关系？如何判断一条直线是否为切线呢？
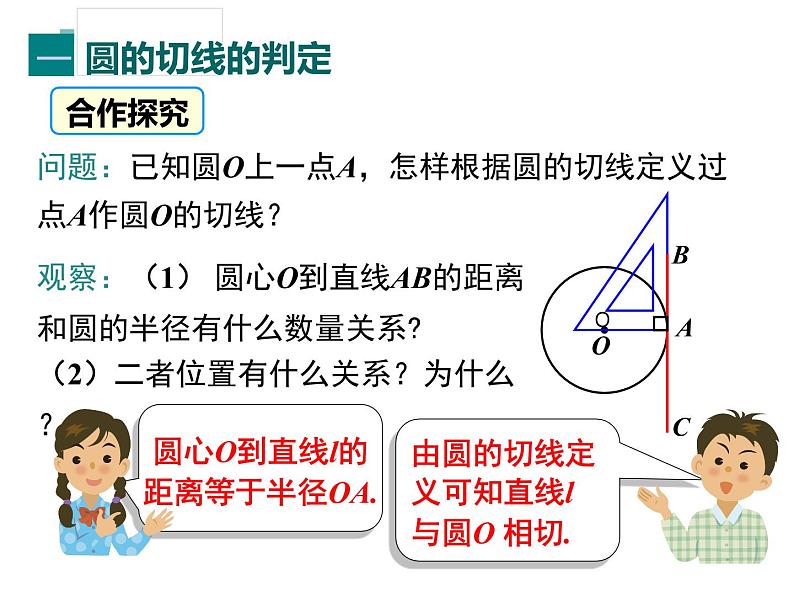
问题：已知圆O上一点A，怎样根据圆的切线定义过点A作圆O的切线？
观察：（1） 圆心O到直线AB的距离和圆的半径有什么数量关系?（2）二者位置有什么关系？为什么？
过半径外端且垂直于半径的直线是圆的切线.
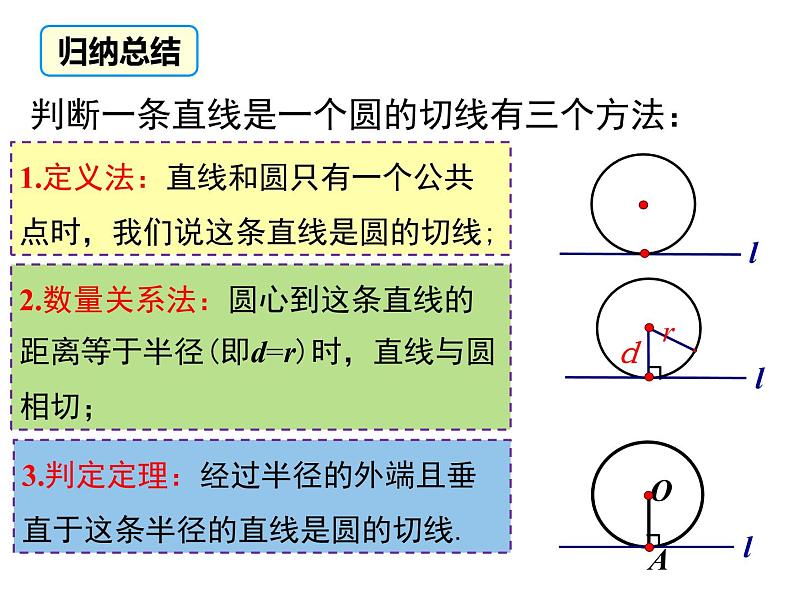
判断一条直线是一个圆的切线有三个方法：
1.定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线;
2.数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；
3.判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线.
下列各直线是不是圆的切线？如果不是，请说明为什么？
(1)不是，因为没有垂直.
(2),(3)不是，因为没有经过半径的外端点A.
例1 已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB.求证：直线AB是⊙O的切线.
证明：连接OC. ∵ OA＝OB,CA＝CB, ∴ OC是等腰△OAB底边AB上的中线.　 ∴ AB⊥OC. ∵ OC是⊙O的半径, ∴ AB是⊙O的切线.
例2 如图,△ABC 中，AB ＝AC ，O 是BC的中点，⊙O 与AB 相切于E.求证：AC 是⊙O 的切线．
分析：根据切线的判定定理，要证明AC是⊙O的切线，只要证明由点O向AC所作的垂线段OF是⊙O的半径就可以了，而OE是⊙O的半径，因此只需要证明OF=OE.
证明：连接OE ，OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E ， ∴OE ⊥ AB.
又∵△ABC 中，AB ＝AC ，　　O 是BC 的中点．
∴AO 平分∠BAC，
∵OE 是⊙O 半径，OF ＝OE，OF ⊥ AC.
∴AC 是⊙O 的切线．
又OE ⊥AB ，OF⊥AC.
(1) 有交点，连半径,证垂直;(2) 无交点，作垂直,证半径.
证切线时辅助线的添加方法
有切线时常用辅助线添加方法
见切点，连半径，得垂直.
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
如图是一张三角形的铁皮，工人师傅要从中截下一块圆形的用料，怎样才能使截下的圆的面积尽可能大呢？
问题1 如果最大圆存在，它与三角形三边应有怎样的位置关系？
最大的圆与三角形三边都相切
问题:在这块三角形铁皮上还能截下更大的圆吗?
问题2 如何求作一个圆，使它与已知三角形的三边都相切？
(1) 如果半径为r的☉I与△ABC的三边都相切，那么圆心I应满足什么条件？
(2) 在△ABC的内部，如何找到满足条件的圆心I呢？
作法：1.作∠B和∠C的平分线BM和CN，交点为O.2.过点O作OD⊥BC.垂足为D.3.以O为圆心，OD为半径作圆O.
已知：△ABC.求作：与△ABC的各边都相切的圆.
步骤：作角平分线→定内心→定半径→作圆
与△ABC的三条边都相切的圆有几个？
因为∠B和∠C的平分线的交点只有一个,并且交点O到△ABC三边的距离相等且唯一，所以与△ABC三边都相切的圆有且只有一个.
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
2.三角形的内心就是三角形的三条角平分线的交点.
1.三角形的内心到三角形的三边的距离相等.
⊙O是△ABC的内切圆，点O是△ABC的内心.
3.三角形的内心一定在三角形的内部
4.内心与顶点连线平分内角。
*重心：三角形的三条中线交于一点，这点到 顶点的距离是它到对边中点距离的2倍.该点叫做三角形的重心. *外心：三角形的三边的垂直平分线交于一点.该点叫做三角形的外心.到三个顶点的距离相等。*垂心：三角形的三条高交于一点.该点叫做三角形的垂心. *内心：三角形的三内角平分线交于一点.该点叫做三角形的内心.到三边的距离相等。
例3： △ABC中，⊙O是△ABC的内切圆，∠ A=70°，求∠ BOC的度数。
∴∠ABC+∠ACB=180°-∠ A=110°
∵⊙O是△ABC的内切圆
∴BO,CO分别是∠ABC和∠ACB的平分线
∴∠ BOC=180°-(∠ OBC+∠OCB) =180°- ( ∠ABC +∠ACB) =180° - ×110° = 125°.
例4：如图，直角三角形的两直角边分别是a、b,斜边为c，则其内切圆的半径r为___________（以含a、b、c的代数式表示r）.
解析：过点O分别作AC，BC，AB的垂线，垂足分别为D，E，F.
则AD=AC-DC=b-r,
BF=BC-CE=a-r,
因为AF=AD，BF=BE，AF+BF=c,
所以a-r+b-r=c,
当△ABC为直角三角形，a,b为直角边时,△ABC的内切圆的半径
例5：如图，△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.
解：设△ABC的内切圆与三边相切于D、E、F，
连接OA、OB、OC、OD、OE、OF，
则OD⊥AB，OE⊥BC，OF⊥AC.
∴S△ABC＝S△AOB＋S△BOC ＋S△AOC
1.判断下列命题是否正确.⑴ 经过半径外端的直线是圆的切线.⑵ 垂直于半径的直线是圆的切线.⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线.⑷ 和圆只有一个公共点的直线是圆的切线.(5)三角形的内心是三角形三个角平分线的交点.(6) 三角形的内心到三角形各边的距离相等. (7)三角形的内心一定在三角形的内部.
2.如图，⊙O内切于△ABC，切点D、E、F分别在BC、AB、AC上．已知∠B＝50°，∠C＝60°，连接OE，OF，DE，DF，那么∠EDF等于(　　)A．40°B．55°C．65°D．70°
4.如图，在⊙O中，AB=OA，P是半径OB延长线上一点，且PB=OB，PA与⊙O的位置关系是________.
3.如图，点A，B，D在⊙O上，∠A=25°，OD的延长线交直线BC于点C，且∠OCB=40°，直线BC与⊙O的位置关系为_________.
6.如图，已知⊙O是边长为2的等边△ABC的内切圆，则⊙O的面积为_________.
5.如图，已知△ABC的内切圆⊙O与BC边相切于点D，连接OB，OD.若∠ABC=40°，则∠BOD的度数是_________.
7.如图，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连接BC，BC平分∠ABD.求证：CD为⊙O的切线.
证明 ∵BC平分∠ABD，
∴∠OBC=∠DBC.
∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
8.如图，在△ABC中，AB=AC，AB是直径，BC与⊙O相交于点D，DE切⊙O于点D.求证：DE⊥AC.
证明：连接OP. ∵AB=AC,∴∠B=∠C. ∵OB=OP，∴∠B=∠OPB， ∴∠OPB=∠C. ∴OP∥AC. ∵PE⊥AC， ∴PE⊥OP. ∴PE为⊙O的切线.
9.如图,△ABC中，AB=AC，以AB为直径的⊙O交边BC于P， PE⊥AC于E. 求证:PE是⊙O的切线.
10.如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M.求证：CD与⊙O相切．
证明：连接OM，过点O作ON⊥CD于点N，∵⊙O与BC相切于点M，∴OM⊥BC.又∵ON⊥CD，O为正方形ABCD对角线AC上一点，∴OM＝ON，∴CD与⊙O相切．
如图，已知E是△ABC的内心，∠A的平分线交BC于点F，且与△ABC的外接圆相交于点D.
(1)证明：∵E是△ABC的内心，∴∠ABE＝∠CBE，∠BAD＝∠CAD.又∵∠CBD＝∠CAD，∴∠BAD＝∠CBD.∴∠CBE＋∠CBD＝∠ABE＋∠BAD.即∠DBE＝∠DEB，故BD＝ED；
(1)求证：BD＝ED；
(2)若AD＝8cm，DF∶FA＝1∶3.求DE的长．
(2)解：∵AD＝8cm，DF∶FA＝1∶3，∴DF＝ AD＝ ×8＝2(cm)．∵∠CBD＝∠BAD，∠D＝∠D，∴△BDF∽△ADB，∴ , ∴BD2＝AD·DF＝8×2＝16，∴BD＝4cm，又∵BD＝DE，∴DE＝4cm.
切线的判定及三角形的内切圆
经过半径的外端并且垂直于这条半径的直线是圆的切线.
与三角形三边都相切的圆叫作三角形的内切圆.