初中数学北师大版九年级下册6 直线与圆的位置关系课文内容ppt课件

这是一份初中数学北师大版九年级下册6 直线与圆的位置关系课文内容ppt课件，共34页。PPT课件主要包含了⑴点在圆内，⑵点在圆上，⑶点在圆外，切线性质的证明等内容，欢迎下载使用。
1.理解直线与圆有相交、相切、相离三种位置关系.2.能根据圆心到直线的距离d和圆的半径r之间的数量关系，判断出直线与圆的位置关系.3.理解并掌握圆的切线的性质定理.
重点：直线和圆的位置关系,切线的性质定理及其运用它们解决一些具体的题目 难点：由上节课点和圆的位置关系迁移并运动直线导出直线和圆的位置关系的三个对应等价.
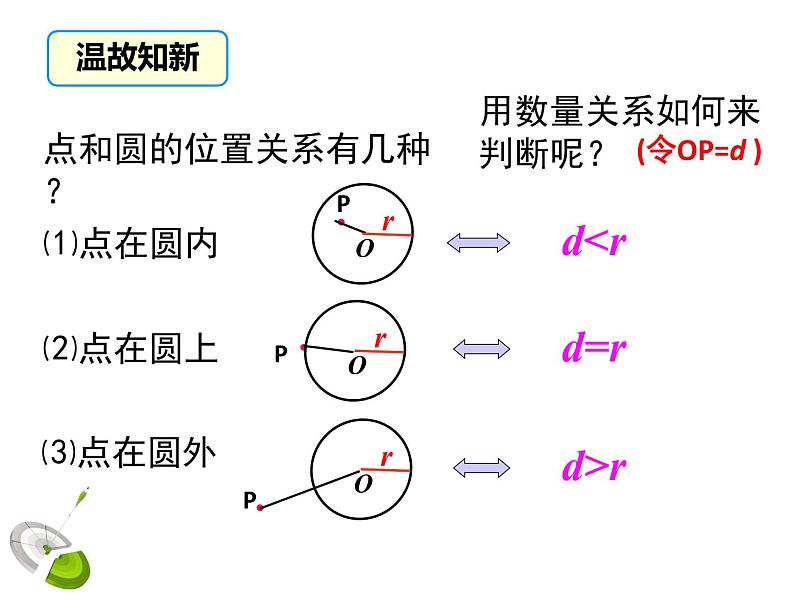
点和圆的位置关系有几种？
用数量关系如何来判断呢？
问题1 如果我们把太阳看成一个圆，地平线看成一条直线，那你能根据直线和圆的公共点个数想象一下，直线和圆有几种位置关系吗？
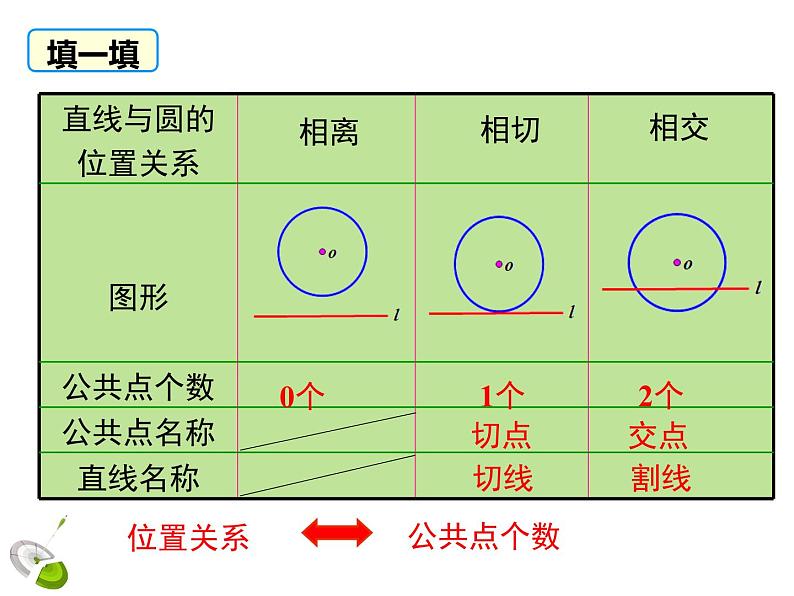
问题2 请同学在纸上画一条直线l，把硬币的边缘看作圆，在纸上移动硬币，你能发现直线和圆的公共点个数的变化情况吗？公共点个数最少时有几个？最多时有几个？
公共点个数最少时有0个，最多时有2个.
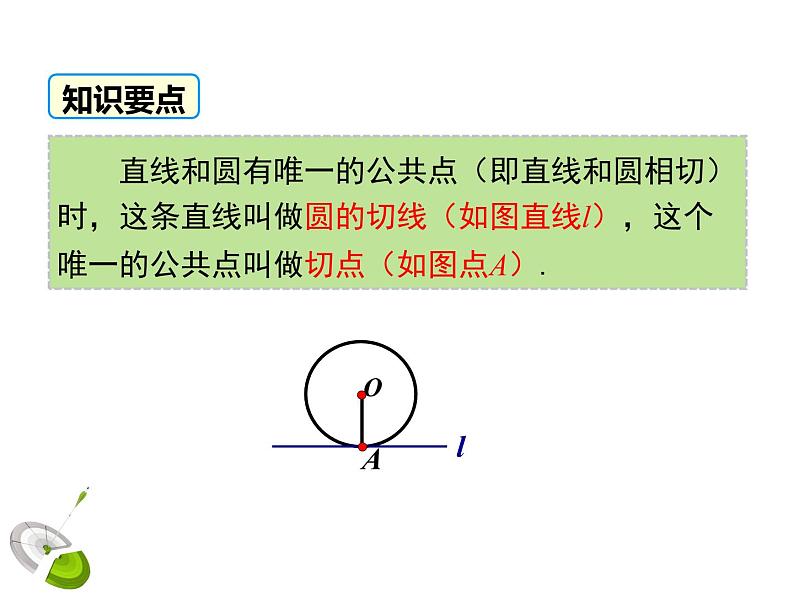
直线和圆有唯一的公共点（即直线和圆相切）时，这条直线叫做圆的切线（如图直线l），这个唯一的公共点叫做切点（如图点A）.
直线与圆最多有两个公共点.若直线与圆相交，则直线上的点都在圆上. 若A是☉O上一点，则直线AB与☉O相切. ④若C为☉O外一点，则过点C的直线与☉O相交或相离. ⑤直线a 和☉O有公共点，则直线a与☉O相交.
问题1 刚才同学们用硬币移近直线的过程中，除了发现公共点的个数发生了变化外，还发现有什么量也在改变？它与圆的半径有什么样的数量关系呢？
圆心到直线的距离在发生变化；首先距离大于半径，而后距离等于半径，最后距离小于半径.
问题2 怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢？
（用圆心O到直线的距离d与圆的半径r的关系来区分）
判定直线与圆的位置关系的方法有____种：
（1）根据定义，由__________________的个数来判断；
（2）根据性质，由_____________________ ______________的关系来判断。
在实际应用中，常采用第二种方法判定。
0cm≤d < 5cm
思考：如图，如果直线l是⊙O 的切线，点A为切点，那么OA与l垂直吗？
证明：∵右图是轴对称图形,直线AB是对称轴,∴沿直线AB对折图形时,AC与AD重合, ∠BAC与∠BAD互为邻补角。∴∠BAC=∠BAD=90°。
直径AB与直线CD要么垂直,要么不垂直.
（1）假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
（2）则OM 5 C. r = 5 D. r ≥ 53. ⊙O的最大弦长为8，若圆心O到直线l的距离为d=5，则直线l与⊙O .4. ⊙O的半径为5,直线l上的一点到圆心O的距离是5，则直线l与⊙O的位置关系是（ ）A. 相交或相切 B. 相交或相离 C. 相切或相离 D. 上三种情况都有可能
6.如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（ ）A．40° B．35° C．30° D．45°
8.在平面直角坐标系中，以点（3，2）为圆心，3为半径的圆，一定（ ）A.与x轴相切，与y轴相切 B.与x轴相切，与y轴相交C.与x轴相交，与y轴相切 D.与x轴相交，与y轴相交
9.如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心坐标为（-3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（ ） A.1 B.1或5 C.3 D.5
10.如图，直线AB是⊙O的切线，C为切点，OD∥AB交⊙O于点D，点E在⊙O上，连接OC，EC，ED，则∠CED的度数为（ ）A.30° B.35° C.40° D.45°
11.如图，已知∠AOB=30°，M为OA边上一点，以点M为圆心，2 cm为半径作⊙M.若点M在OA边上运动，则OM=_______cm时，⊙M与OB相切.
12.在直角坐标系中，⊙M的圆心坐标是（m,0），半径是2，如果⊙M与y轴所在的直线相切，那么m=_____；如果⊙M与y轴所在的直线相交，那么m的取值范围是____________.
(2)解：由(1)可知OA=OC=AC， ∴△OAC为等边三角形， ∴∠AOB=60°， ∴在Rt△OAB中， ∠B=90°-60°=30°.
14.已知⊙O的半径r =7cm,直线l1 // l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离.
（1） l2与l1在圆的同一侧： m=9-7=2 cm
（2）l2与l1在圆的两侧： m=9+7=16 cm
解：设 l2与l1的距离为m，
在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm. (1) 以点C为圆心作圆，当半径为多长时，AB与圆C相切？
解：过C作CD⊥AB，垂足为D.
根据三角形的面积公式有
因此，当半径长为2.4cm时，AB与圆C相切.
记住：斜边上的高等于两直角边的乘积除以斜边.
(2)以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？① r=2cm；② r=2.4cm； ③ r=3cm．
解：由(1)可知圆心C到AB的距离d=2.4cm.
所以 ①当r=2cm时,
②当r=2.4cm时,有d=r.
③当r=3cm时，有d