数学八年级下册1. 平面直角坐标系教学课件ppt

这是一份数学八年级下册1. 平面直角坐标系教学课件ppt，共43页。PPT课件主要包含了复习引入，情境引入，第3排，第2列，做一做，合作探究，想一想，概念学习，试一试，典例精析等内容，欢迎下载使用。

在数轴上,如何确定一个点的位置呢?
A点记作-2,B点记作3.也就是说,
在数轴上一般用一个数据就可以表示一个点的位置．
小明父子俩周末去电影院看国产大片《战狼2》，买了两张票去观看，座位号分别是3排6号和6排3号.怎样才能既快又准地找到座位？
思考1 在班里老师想找一个学生，你知道是谁吗？
思考2 你认为确定一个位置需要几个数据？
提示1：只给一个数据“第２列”，你能确定老师要找的学生是谁吗？
提示2：给出两个数据“第２列，第3排”，你能确定是谁了吗？
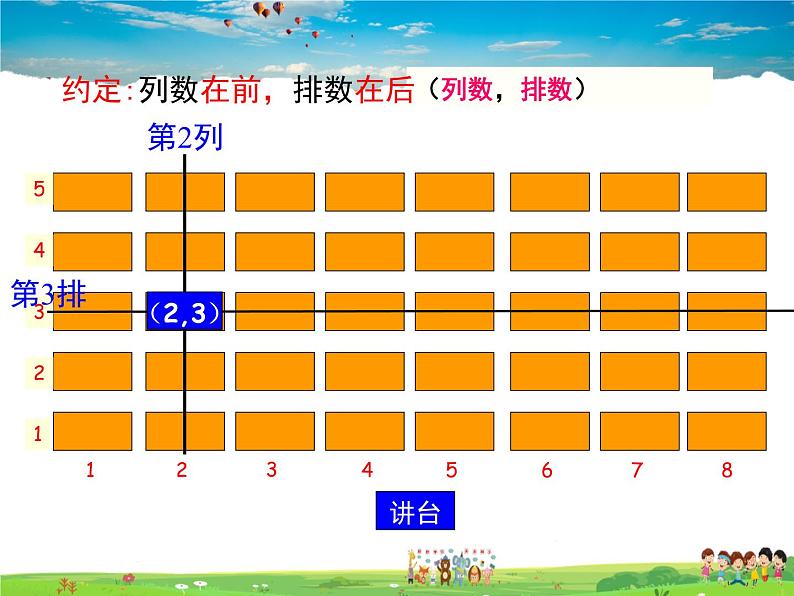
约定:列数在前，排数在后
（1）在电影票上“6排3号”与“3排6号”中的“6”的含义有什么不同？你能找到它们对应的位置吗？
（2）如果将“6排3号”简记作（6，3），那么“3排6号”如何表示？（5，6）表示什么含义？ （6，5）呢?
(3) 在只有一层的电影院内，确定一个座位一般需要几个数据？
答:两个数据:排数和号数.
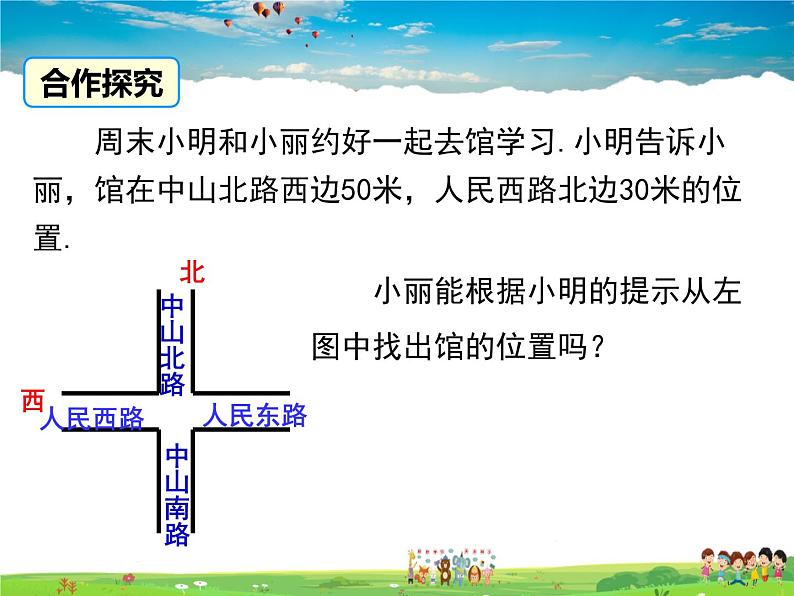
小丽能根据小明的提示从左图中找出馆的位置吗？
周末小明和小丽约好一起去馆学习.小明告诉小丽，馆在中山北路西边50米，人民西路北边30米的位置.
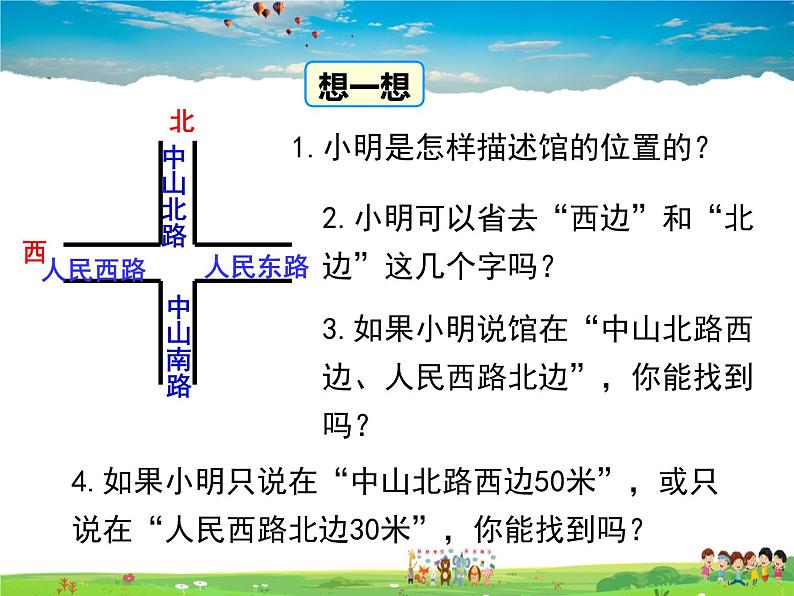
4.如果小明只说在“中山北路西边50米”，或只说在“人民西路北边30米”，你能找到吗？
1.小明是怎样描述馆的位置的？
2.小明可以省去“西边”和“北边”这几个字吗？
3.如果小明说馆在“中山北路西边、人民西路北边”，你能找到吗？
若将中山路与人民路看成两条互相垂直的数轴，十字路口为它们的公共原点，这样就形成了一个平面直角坐标系.
水平方向的数轴称为x轴或横轴，垂直方向的数轴称为y轴或纵轴，它们称为坐标轴.两轴交点O称为原点.
在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系，如图所示.
思考：如何在平面直角坐标系中表示点呢？
这样P点的横坐标是-2，纵坐标是3，规定把横坐标写在前，纵坐标在后，记作：P(-2，3)P(-2，3)就叫做点P在平面直角坐标系中的坐标，简称点P的坐标.
思考：如图点P如何表示呢？
后由P点向y轴画垂线，垂足N在y轴上对应的数是3. 称为P点的纵坐标.
先由P点向x轴画垂线，垂足M在x轴上对应的数是-2；称为P点的横坐标.
1. 找出点Ａ的坐标.
(1)过点Ａ作x轴的垂线，垂足在x轴上对应的数是４；(2)过点Ａ作y轴的垂线，垂足在y轴上对应的数是３； 点Ａ的坐标为（４，３）
2. 在平面直角坐标系中找点A(3,-2)
由坐标找点的方法： (1)先找到表示横坐标与纵坐标的点； (2)然后过这两点分别作x轴与y轴的垂线； (3)垂线的交点就是该坐标对应的点.
例1：写出下图中的多边形ABCDEF各个顶点的坐标.
【答案】A（-2，0） B（0，-3） C（3，-3） D（4，0） E（3，3） F（0，3）
在直角坐标系中描出下列各点：A（4，3）， B（-2，3），C（-4，-1），D（2，-2）.
在平面直角坐标系中，两条坐标轴（即横轴和纵轴）把平面分成如图所示的Ⅰ，Ⅱ ，Ⅲ，Ⅳ四个区域.
分别称为第一，二，三，四象限.
注意：坐标轴上的点不属于任何一个象限.
活动1: 观察坐标系,填写各象限内的点的坐标的特征：
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,-1), D(2.5,-2), E(0,-4)所在的象限吗？你的方法又是什么？
交流：不看平面直角坐标系,你能迅速说出(-5,0),(0,-5),(3,0),(0,3),(0,0)所在的位置吗？你的方法又是什么？
活动2.观察坐标系,填写坐标轴上的点的坐标的特征：
例2：在平面直角坐标系中，描出下列各点，并指出它们分别在哪个象限. A(5，4)，B(-3，4)，C (-4 ，-1)，D(2，-4).
例3 设点M(a，b)为平面直角坐标系内的点．(1)当a>0，b<0时，点M位于第几象限？(2)当ab>0时，点M位于第几象限？(3)当a为任意有理数，且b<0时，点M位于第几象限？
解：(1)点M在第四象限；(2)可能在第一象限(a>0，b>0)或者在第三象限(a<0，b<0)；(3)可能在第三象限(a<0，b<0)或者第四象限(a>0，b<0)或者y轴负半轴上(a=0，b<0)．
已知在平面直角坐标系中，点P(m，m－2)在第一象限内，则m的取值范围是________．
解析：根据第一象限内点的坐标的符号特征，横坐标为正，纵坐标为正，可得关于m的一元一次不等式组解得m＞2.
【方法总结】求点的坐标中字母的取值范围的方法：根据各个象限内点的坐标的符号特征，列出关于字母的不等式或不等式组，解不等式或不等式组即可求出相应字母的取值范围．
例4 点A(m＋3，m＋1)在x轴上，则A点的坐标为(　　)A．(0，－2) B．(2，0) C．(4，0) D．(0，－4)
【解析】点A(m＋3，m＋1)在x轴上，根据x轴上点的坐标特征知m＋1＝0，求出m的值代入m＋3中即可．
【方法总结】坐标轴上的点的坐标特点：x轴上的点的纵坐标为0，y轴上的点的横坐标为0.根据点所在坐标轴确定字母取值，进而求出点的坐标．
问题1：已知点A和一条直线MN，你能画出这个点关于已知直线的对称点吗?
∴A′就是点A关于直线MN的对称点.
（2）延长AO至A′,使OA′=AO.
（1）过点A作AO⊥MN，垂足为点O，
问题2：如图，在平面直角坐标系中你能画出点A关于x轴的对称点吗?
做一做：在平面直角坐标系中画出下列各点关于x轴的对称点.
( , )
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
练一练:1.点P(-5, 6)与点Q关于x轴对称，则点Q的坐标为__________.2.点M(a, -5)与点N(-2, b)关于x轴对称，则a=_____, b =_____.
(- 5 , -6 )
问题3：如图，在平面直角坐标系中你能画出点A关于y轴的对称点吗?
做一做：在平面直角坐标系中画出下列各点关于y轴的对称点.
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
练一练:1.点P(-5, 6)与点Q关于y轴对称，则点Q的坐标为__________.2.点M(a, -5)与点N(-2, b)关于y轴对称，则a=_____, b =_____.
如图，分别写出以下各点关于原点对称的点的坐标.
思考：关于原点对称的两点的坐标又有何特征呢？
A(3，1),B(1，3),P(0，3),C(-1，3),D(-3，1)M(0，3)
E(-3，-1),F(-1，-3),Q(0，-3),G(1，-3),H(3，-1)N(0，-3)
关于原点对称的两点，横坐标和纵坐标都互为相反数.
点（4，3）与点（4，- 3）的关系是（ ） A.关于原点对称 B.关于 x轴对称 C.关于 y轴对称 D.不能构成对称关系
例5 已知点A(2a－b，5＋a)，B(2b－1，－a＋b)．(1)若点A、B关于x轴对称，求a、b的值；(2)若A、B关于y轴对称，求(4a＋b)2018的值．
解：(1)∵点A、B关于x轴对称，∴2a－b＝2b－1，5＋a－a＋b＝0，解得a＝－8，b＝－5； (2)∵A、B关于y轴对称，∴2a－b＋2b－1＝0，5＋a＝－a＋b，解得a＝－1，b＝3，∴(4a＋b)2018＝1.
例6 已知点P(a＋1，2a－1)关于x轴的对称点在第一象限，求a的取值范围．
解：依题意得P点在第四象限，
方法总结：解决此类题，一般先判断出点或对称点所在的象限，再由各象限内点的坐标的符号，列不等式(组)求解．
1.如图，点A的坐标为( )A. ( -2，3)B. ( 2，-3)C . ( -2，-3)D . ( 2，3)
2.如图，点A的坐标为 ，点B的坐标为 .
3.在 y轴上的点的横坐标是______，在 x轴上的点的纵坐标是 ______.4.点 M（- 8，12）到 x轴的距离是_______，到 y轴的距离是 _________ .
5.设点M（x，y）在第二象限，且|x|=2，|y|=3，则点M关于y轴的对称点的坐标是（　　）A．（2，3） B．（－2，3） C．（－3，2） D．（－3，－2）
6.如图，在平面直角坐标系中，点P(－1，2)关于直线x=1的对称点的坐标为（　　）A．（1，2） B．（2，2） C．（3，2） D．（4，2）
A（3，6）B（0，－8）C（－7，－5）D（－6，0）E（－，5）F（5，－6）G（0，0）
7.下列各点分别在坐标平面的什么位置上？
8.已知点P(a－2，2a+8)，分别根据下列条件求出点P的坐标．（1）点P在x轴上； （2）点P在y轴上；
解：（1）∵点P(a－2，2a+8)在x轴上，∴2a+8=0，解得a=－4，故a－2=－4－2=－6，则P(－6，0)；（2）∵点P(a－2，2a+8)在y轴上，∴a－2=0，解得a=2，故2a+8=2×2+8=12，则P(0，12)；
8.已知点P(a－2，2a+8)，分别根据下列条件求出点P的坐标．（3）点Q的坐标为（1，5），直线PQ∥y轴；
解：∵点Q的坐标为(1，5)，直线PQ∥y轴， ∴a－2=1， 解得 a=3， 故2a+8=14，则P(1，14)；
8.已知点P(a－2，2a+8)，分别根据下列条件求出点P的坐标． （4）点P到x轴、y轴的距离相等．
解：∵点P到x轴、y轴的距离相等， ∴a－2=2a+8或a－2+2a+8=0， 解得 a=－10或a=－2， 故当a=－10时，则a－2=－12，2a+8=－12， 则P(－12，－12)； 故当a=－2时，则a－2=－4，2a+8=4， 则P(－4，4)．综上所述，P(－12，－12)，(－4，4)．