数学八年级下册18.2 平行四边形的判定教案配套课件ppt

这是一份数学八年级下册18.2 平行四边形的判定教案配套课件ppt，共18页。PPT课件主要包含了从边考虑，从角考虑，从对角线考虑，平行四边形的判定方法，复习引入，tcm，12-tcm，15-2tcm，cm2等内容，欢迎下载使用。

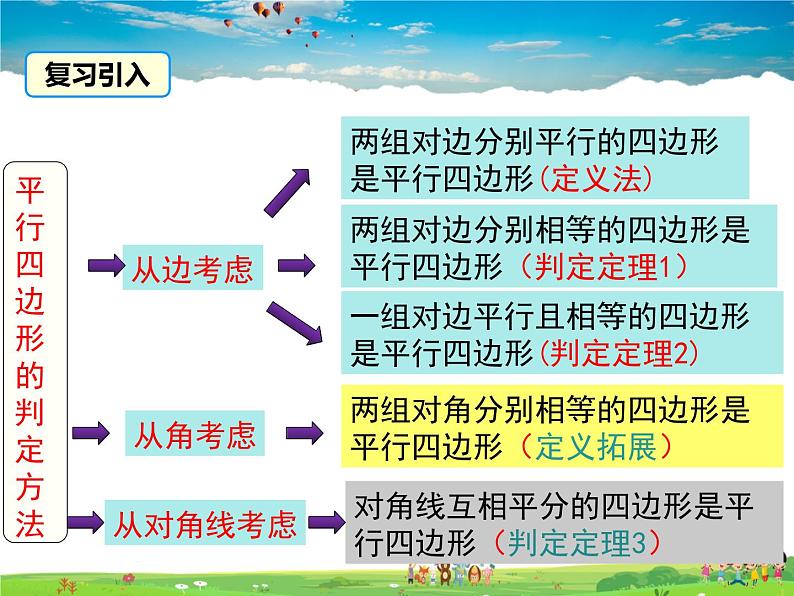
两组对边分别平行的四边形是平行四边形(定义法)
一组对边平行且相等的四边形是平行四边形(判定定理2)
两组对边分别相等的四边形是平行四边形（判定定理1）
两组对角分别相等的四边形是平行四边形（定义拓展）
对角线互相平分的四边形是平行四边形（判定定理3）
证明：∵四边形AEFD和EBCF都是平行四边形，∴AD EF，EF BC.∴AD BC.∴四边形ABCD是平行四边形.
问题 四边形AEFD和EBCF都是平行四边形，求证四边形ABCD 是平行四边形.
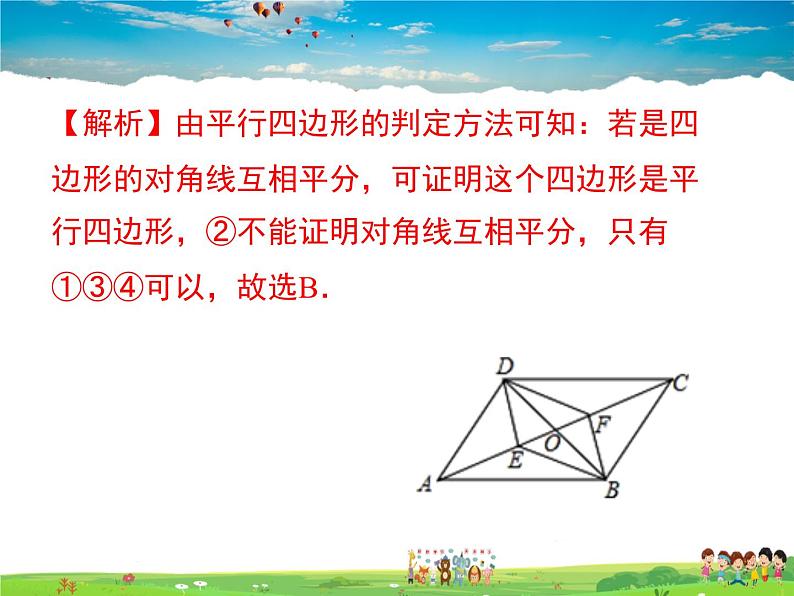
例1.如图，在平行四边形ABCD中，对角线AC、BD相交于点O，E、F是对角线AC上的两点，给出下列四个条件：①AE=CF；②DE=BF；③∠ADE=∠CBF；④∠ABE=∠CDF．其中不能判定四边形DEBF是平行四边形的有（　　）A．0个 B．1个 C．2个 D．3个
【解析】由平行四边形的判定方法可知：若是四边形的对角线互相平分，可证明这个四边形是平行四边形，②不能证明对角线互相平分，只有①③④可以，故选B．
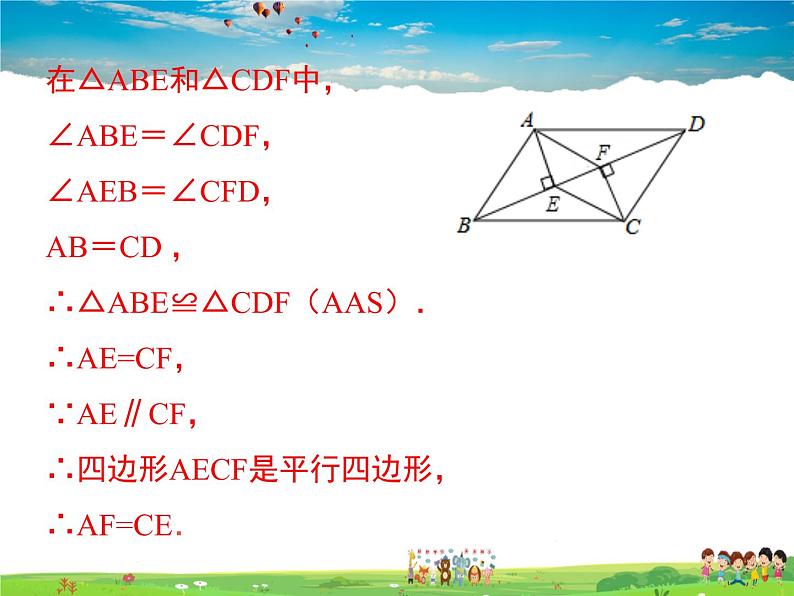
例2 如图，在 ABCD中，AE⊥BD于E，CF⊥BD于F，连接AF，CE．求证：AF=CE．
证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴∠ABE=∠CDF．又∵AE⊥BD，CF⊥BD，∴∠AEB=∠CFD=90°，AE∥CF，
在△ABE和△CDF中，∠ABE＝∠CDF， ∠AEB＝∠CFD，AB＝CD ，∴△ABE≌△CDF（AAS）．∴AE=CF，∵AE∥CF，∴四边形AECF是平行四边形，∴AF=CE．
例3.如图，AB、CD相交于点O，AC∥DB，AO＝BO，E、F分别是OC、OD的中点．求证：(1)△AOC≌△BOD；(2)四边形AFBE是平行四边形．
证明：(1)∵AC∥BD，∴∠C＝∠D.又∵∠COA=∠DOB，AO＝BO ，∴△AOC≌△BOD(AAS)；(2)∵△AOC≌△BOD，∴CO＝DO.∵E、F分别是OC、OD的中点，∴EO＝FO.又∵AO＝BO，∴四边形AFBE是平行四边形．
例4.如图，在四边形ABCD中，AD∥BC，AD=12cm，BC=15cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，点P，Q同时出发，设运动时间为t(s)．（1）用含t的代数式表示： AP=_____； DP=________； BQ=________；CQ=________；
（2）当t为何值时，四边形APQB是平行四边形？
解：根据题意有AP=tcm，BQ=(15-2t)cm．∵AD∥BC，∴当AP=BQ时，四边形APQB是平行四边形．∴t=15-2t，解得t=5．∴t=5s时四边形APQB是平行四边形；
解：由题意知CQ=2tcm，PD=(12-t)cm，∵AD∥BC，∴当PD=QC时，四边形PDCQ是平行四边形．即12-t=2t，解得t=4s，∴当t=4s时，四边形PDCQ是平行四边形．
（3）当t为何值时，四边形PDCQ是平行四边形？
1.(1)在□ABCD中，∠A=150°，AB=8cm,BC=10cm,则S □ABCD= .
提示：①过点A作AE⊥BC于E;②直角三角形中，30°角所对的边等于斜边的一半.
(2)若点P是□ABCD的边AD上任意一点，那么△PBC的面积是 .
提示：△PBC与□ABCD是同底等高.
2.如图，▱ABCD 中． EF∥GH∥BC，MN∥AB，则图中平行四边形的个数是（　　）A．13 B．14 C．15 D．18
【解析】根据平行四边形的定义：两组对边分别平行的四边形是平行四边形，如图，则图中的四边形AEOM、AGPM、ABNM、EGPO、EBNO、GBNP、MOFD、MPHD、MNCD、OPHF、ONCF、PNCH、AEFD、AGHD、ABCD、EGHF、EBCF和GBCH都是平行四边形，共18个．故选D．
3.在▱ABCD中，E、F分别在BC、AD上，若想要使四边形AFCE为平行四边形，需添加一个条件，这个条件不可以是（　　）A．AF=CE B．AE=CF C．∠BAE=∠FCD D．∠BEA=∠FCE
4.如图，▱ABCD中，E，F分别为AD，BC边上的点，要使四边形BEDF为平行四边形，需添加一个条件: ______________________________________________.
AE=FC或∠ABE=∠CDF或BE∥DF（答案不唯一）
5.如图，在▱ABCD中，E、F分别为边AD、BC的中点，对角线AC分别交BE，DF于点G、H．求证：AG=CH．
证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADF=∠CFH，∠EAG=∠FCH，∵E、F分别为AD、BC边的中点，∴AE=DE=1/2AD，CF=BF=1/2BC，∴DE∥BF，DE=BF，∴四边形BFDE是平行四边形，
∴BE∥DF，∴∠AEG=∠ADF，∴∠AEG=∠CFH，在△AEG和△CFH中， ∠EAG＝∠FCH AE＝CF ∠AEG＝∠CFH ，∴△AEG≌△CFH（ASA），∴AG=CH．