数学3. 圆周角教学课件ppt

这是一份数学3. 圆周角教学课件ppt，共41页。PPT课件主要包含了复习引入，顶点不在圆上，边AC没有和圆相交，想一想，知识要点，典例精析，测量与猜测，推导与论证，OAOC，∠A∠C等内容，欢迎下载使用。

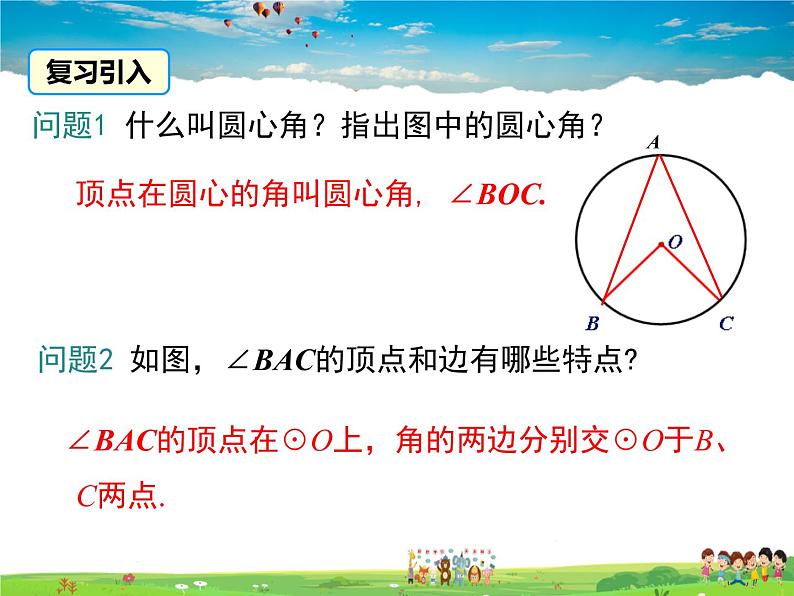
问题1 什么叫圆心角？指出图中的圆心角？
顶点在圆心的角叫圆心角, ∠BOC.
问题2 如图，∠BAC的顶点和边有哪些特点?
∠BAC的顶点在☉O上，角的两边分别交☉O于B、C两点.
思考： 图中过球门A、C两点画圆，球员射中球门的难易程度与他所处的位置B、D、E有关（张开的角度大小）、仅从数学的角度考虑，球员应选择从哪一点的位置射门更有利？
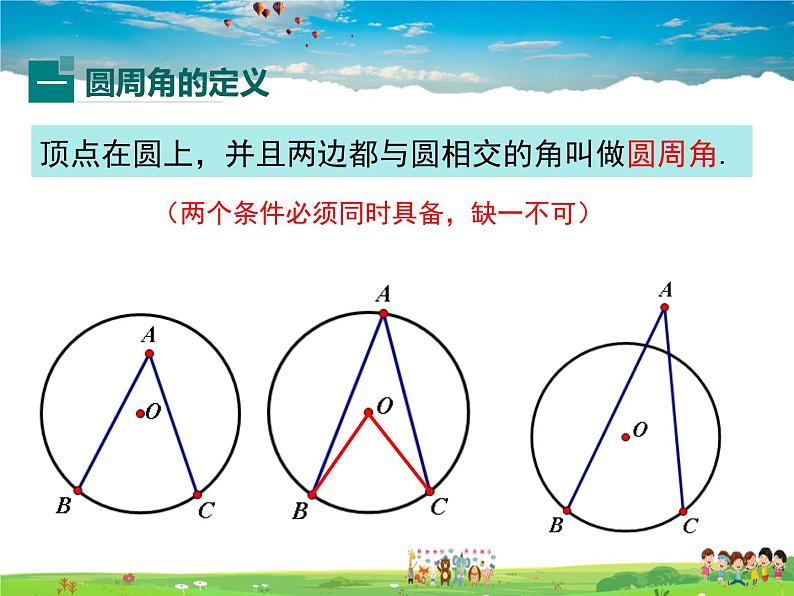
顶点在圆上，并且两边都与圆相交的角叫做圆周角.
（两个条件必须同时具备，缺一不可）
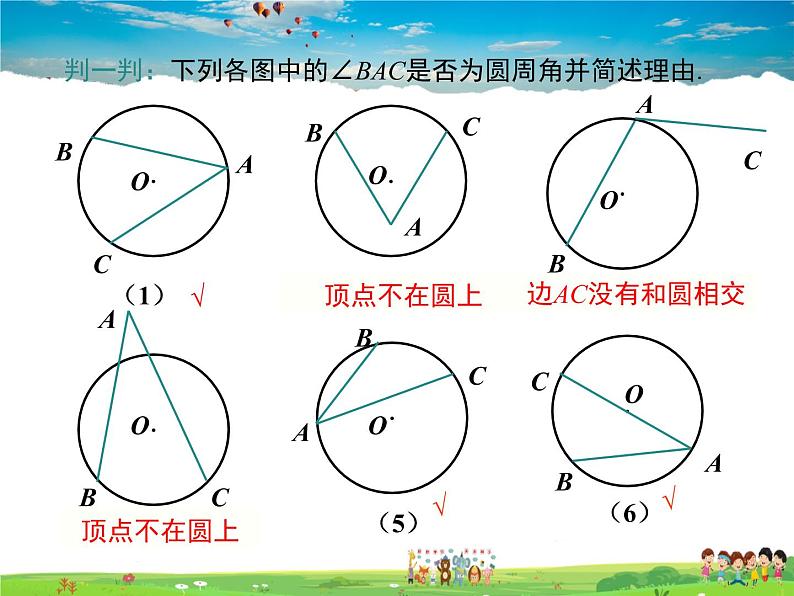
判一判：下列各图中的∠BAC是否为圆周角并简述理由.
如图，线段AB是☉O的直径，点C是 ☉O上的任意一点（除点A、B外），那么，∠ABC就是直径AB所对的圆周角，想一想，∠ACB会是怎样的角？
解：∵OA=OB=OC，∴△AOC、△BOC都是等腰三角形.
∴ ∠OAC=∠OCA，∠OBC=∠OCB.
又∵ ∠OAC+∠OBC+∠ACB=180°.
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.
圆周角和直径的关系： 半圆或直径所对的圆周角都相等，都等于90°.
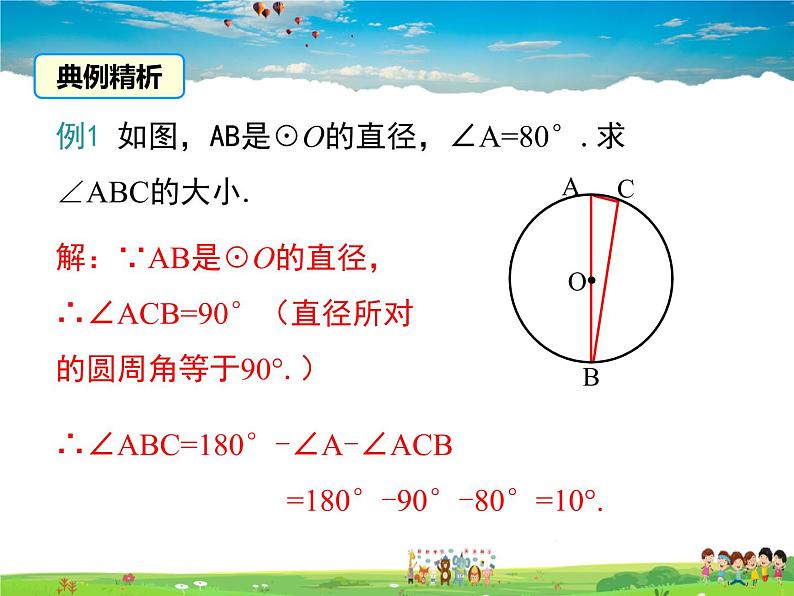
例1 如图，AB是☉O的直径，∠A=80°.求∠ABC的大小.
解：∵AB是☉O的直径，∴∠ACB=90°（直径所对的圆周角等于90°.）
∴∠ABC=180°-∠A-∠ACB =180°-90°-80°=10°.
如图，连接BO,CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
圆心O 在∠BAC的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC的外部
圆心O在∠BAC的一边上（特殊情形）
∠BOC= ∠ A+ ∠C
圆心O在∠BAC的内部
问题1 如图，OB，OC都是⊙O的半径，点A ,D 是上任意两点，连接AB，AC，BD，CD.∠BAC与∠BDC相等吗？请说明理由.
(2)若CD是直径，你能求出∠A的度数吗？
圆周角定理： 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半； 相等的圆周角所对的弧也相等.
推论1：90°的圆周角所对的 弦是直径.
试一试：1.如图，点A、B、C、D在☉O上，点A与点D在点B、C所在直线的同侧，∠BAC=35º.
(1)∠BOC= º，理由是 ;(2)∠BDC= º，理由是 .
一条弧所对的圆周角等于它所对的圆心角的一半
(1)完成下列填空： ∠1= . ∠2= . ∠3= . ∠5= .
2.如图，点A、B、C、D在同一个圆上，AC、BD为四边形ABCD的对角线.
例2 如图，分别求出图中∠x的大小.
解：(1)∵同弧所对圆周角相等，∴∠x=60°.
∵同弧所对圆周角相等，
∴∠ABF=∠D=20°，∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
例3：如图，⊙O的直径AC为10cm，弦AD为6cm.（1）求DC的长；
（2）若∠ADC的平分线交⊙O于B, 求AB、BC的长．
在Rt△ABC中，AB2+BC2=AC2，
(2)∵ AC是直径, ∴ ∠ABC=90°. ∵BD平分∠ADC, ∴∠ADB=∠CDB.又∵∠ACB=∠ADB , ∠BAC=∠BDC . ∴ ∠BAC=∠ACB, ∴AB=BC.
如图，BD是⊙O的直径，∠CBD＝30°，则∠A的度数为(　　)A．30° B．45° C．60° D．75°
解析：∵BD是⊙O的直径，∴∠BCD＝90°.∵∠CBD＝30°，∴∠D＝60°，∴∠A＝∠D＝60°.故选C.
方法总结：在圆中，如果有直径，一般要找直径所对的圆周角，构造直角三角形解题．
例4 如图,AB是⊙O的直径,弦CD交AB于点P,∠ACD=60°,∠ADC=70°.求∠APC的度数.
解:连接BC,则∠ACB=90°,
∠DCB＝∠ACB－∠ACD＝90°－60°=30°.
又∵∠BAD=∠DCB=30°,
∴∠APC=∠BAD＋∠ADC＝30°＋70°＝100°.
如果一个圆经过一个多边形的各个顶点，这个圆就叫作这个多边形的外接圆.这个多边形叫做圆的内接多边形.
如图，四边形ABCD为⊙O的内接四边形，⊙O为四边形ABCD的外接圆.
猜想：∠A与∠C, ∠B与∠D之间的关系为：
∠A+ ∠C=180º，∠B+ ∠D=180º
想一想：如何证明你的猜想呢？
∵ 弧BCD和弧BAD所对的圆心角的和是周角，
∴∠A＋∠C＝180°，
同理∠B＋∠D＝180°，
推论：圆的内接四边形的对角互补.
∠BCD＋∠DCE＝180°.
图中∠A与∠DCE的大小有何关系？
推论：圆的内接四边形的任何一个外角都等于它的内对角.
1．四边形ABCD是⊙O的内接四边形，且∠A=110°，∠B=80°，则∠C= ，∠D= .2．⊙O的内接四边形ABCD中，∠A∶∠B∶∠C=1∶2∶3 ，则∠D= .
例5：如图，AB为⊙O的直径，CF⊥AB于E，交⊙O于D，AF交⊙O于G. 求证：∠FGD＝∠ADC.
证明：∵四边形ACDG内接于⊙O，∴∠FGD＝∠ACD.又∵AB为⊙O的直径，CF⊥AB于E，∴AB垂直平分CD，∴AC＝AD，∴∠ADC＝∠ACD，∴∠FGD＝∠ADC.
方法总结：圆内接四边形的性质是沟通角相等关系的重要依据．
如图，在⊙O的内接四边形ABCD中，∠BOD＝120°，那么∠BCD是(　　)A．120° B．100°C．80° D．60°
解析：∵∠BOD＝120°，∴∠A＝60°，∴∠C＝180°－60°＝120°，故选A.
解：设∠A，∠B，∠C的度数分别对于2x，3x，6x，
例6 在圆内接四边形ABCD中， ∠A，∠B，∠C的度数之比是2︰3︰6.求这个四边形各角的度数.
∵四边形ABCD内接于圆，
∴ ∠A+ ∠C=∠B+∠D=180°，
∵2x+6x=180°，
∴ ∠A=45°， ∠B=67.5°， ∠C =135°， ∠D=180°-67.5°=112.5°.
1.判断（1）同一个圆中等弧所对的圆周角相等 （ ）（2）相等的弦所对的圆周角也相等 （ ）（3）同弦所对的圆周角相等 （ ）
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°, 则∠AOB= ．
3.如图，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为（ ） A.30° B.40° C.50° D.60°
【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.
4.如图，四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是（ ） A 115° B 130° C 65° D 50°5.如图，等边三角形ABC内接于⊙O，P是AB上的一点，则∠APB= .
6.如图，已知圆心角∠AOB=100°,则圆周角∠ACB= ，∠ADB= .
7.如图，△ABC的顶点A、B、C都在⊙O上，∠C＝30 °，AB＝2，则⊙O的半径是 .
∵∠C=30 ° ，∴∠AOB=60 °
又∵OA=OB ，∴△AOB是等边三角形
∴OA=OB=AB=2，即半径为2.
∴∠ACB=2∠BAC
8. 如图，OA，OB，OC都是⊙O的半径，∠AOB=2∠BOC. 求证：∠ACB=2∠BAC.
∠AOB=2∠BOC，
9.船在航行过程中，船长通过测定角数来确定是否遇到暗礁，如图，A、B表示灯塔，暗礁分布在经过A、B两点的一个圆形区域内，优弧AB上任一点C都是有触礁危险的临界点，∠ACB就是“危险角”，当船位于安全区域时，∠α与“危险角”有怎样的大小关系？
解：当船位于安全区域时，即船位于暗礁区域外（即⊙O外） ，与两个灯塔的夹角∠α小于“危险角”.
∵AB是圆的直径，点D在圆上，
∵AB=AC， ∴BD=CD.
∵AD平分顶角∠BAC，即∠BAD=∠CAD，
（同圆或等圆中相等的圆周角所对弧相等）.
解:BD=CD.理由是:连接AD,