北师大版九年级下册第三章 圆4 圆周角和圆心角的关系备课课件ppt

这是一份北师大版九年级下册第三章 圆4 圆周角和圆心角的关系备课课件ppt，共24页。PPT课件主要包含了这节课有何收获等内容，欢迎下载使用。
2.圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。
3.定理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。
1.顶点在圆心的角叫做圆心角.
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
①平分弦（不是直径），②垂直弦，③经过圆心，④平分劣弧， ⑤平分优弧这五个要素中，任意已知其中的两个成立，都能推出其余三个。
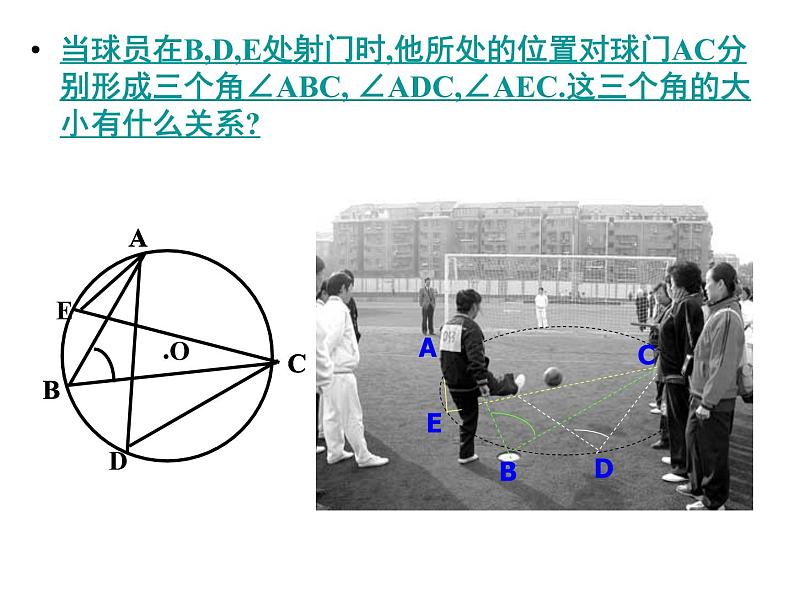
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?
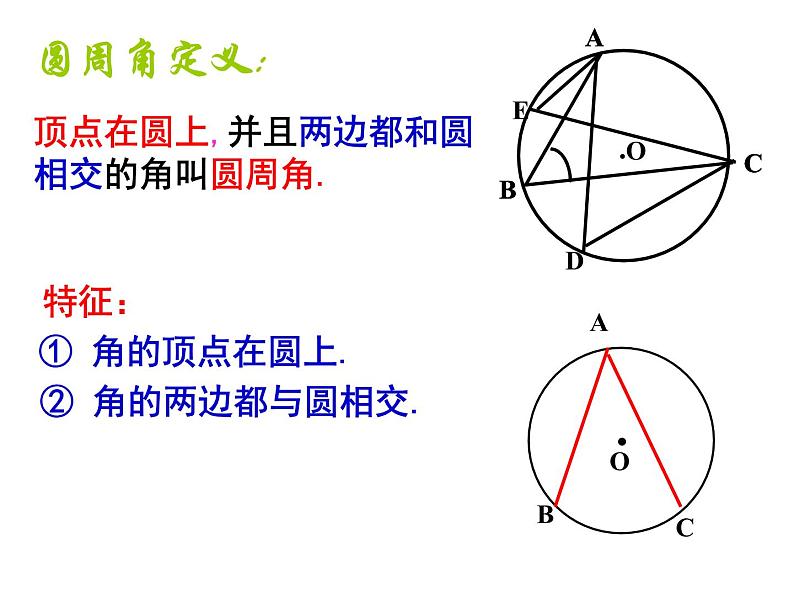
② 角的两边都与圆相交.
圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
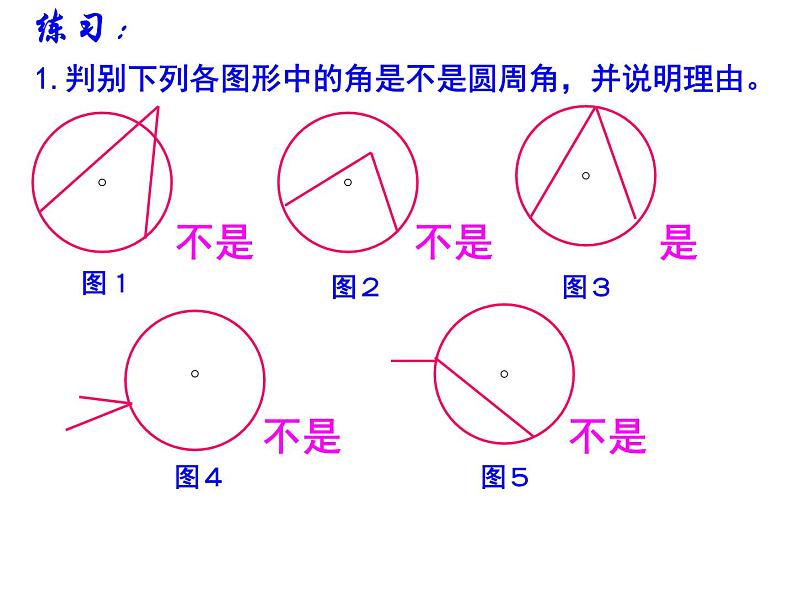
1.判别下列各图形中的角是不是圆周角，并说明理由。
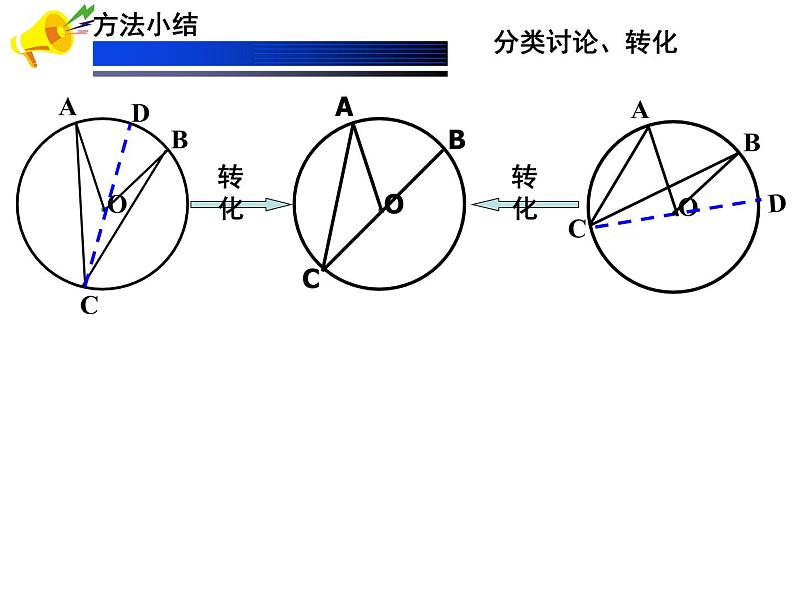
议一议:改变∠AOB的度数，上面的结论仍成立吗？
一条弧所对的圆周角等于它所对的圆心角的一半.
所对的圆周角。这几个圆周角有什么关
系呢？请你与同伴进行交流。
）这些圆周角与圆心角∠
的大小有什么关系？你是怎样
发现的？与同伴进行交流。
如图所示，∠ADB、∠ACB、∠AOB分别是什么角？它们有何共同点？ ∠ADB与∠ACB有什么关系？
同弧 所对的圆周角相等.
都等于这条弧所对的圆心角的一半.
相等的圆周角所对的弧相等.
在射门游戏中，当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?你能用圆周角定理去解决问题。
同弧或等弧所对的圆周角相等。
⑴“同弧或等弧”能否改为“同弦或等弦”？
⑵ “同圆或等圆”这一条件能否省去？
同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等。
如图,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
2.如图，圆心角∠AOB=100°，则∠ACB=___。
3、 如图，在直径为AB的半圆中，O为圆心，C、D为半圆上的两点，∠COD=500，则∠CAD=_________
4、AB、AC为⊙O的两条弦，延长CA到D，使AD=AB，如果∠ADB=350，求∠BOC的度数。
1.如图(1),在⊙O中,∠BAD=50°,求∠C的大小.
2.如图(2),AB是直径,你能确定∠C的度数吗?
(1) (2)
解：在⊙O中，∠BOC=50°
图中有几对相似三角形？
又∵∠AOB=2 ∠BOC
解：∠ACB= 2 ∠BAC，理由:
即∠ACB= 2 ∠BAC
解：∵∠BCD=100°∴优弧所对的圆心角∠BOD=2∠BCD=200°∴劣弧所对的圆心角∠BOD=360°-200°=160°
3.为什么电影院的座位排列呈弧形，说一说这设计的合理性。
答：有些电影院的座位排列呈圆弧形，这样设计的理由是尽量保证同排的观众视角相等。
4.船在航行过程中，船长通过测定角数来确定是否遇到暗礁，如图，A、B表示灯塔，暗礁分布在经过A、B两点的一个圆形区域内，优弧AB上任一点C都是有触礁危险的临界点，∠ACB就是“危险角”，当船位于安全区域时，∠α与“危险角”有怎样的大小关系？
解：当船位于安全区域时，即船位于暗礁区域外（即⊙O外） ，与两个灯塔的夹角∠α小于“危险角” 。
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
相等的弦所对的弧不一定相等.