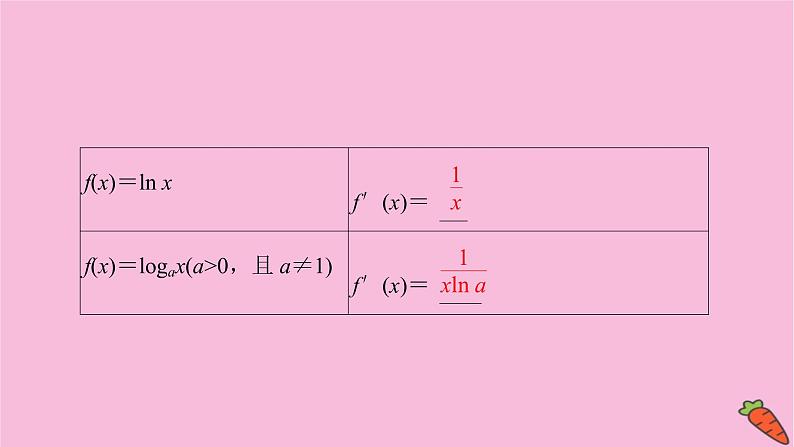
2022届新高考数学人教版一轮课件：第二章 第九节　导数概念及其运算

这是一份2022届新高考数学人教版一轮课件：第二章 第九节　导数概念及其运算，共44页。PPT课件主要包含了x0fx0，切线的斜率，αxα－1，cosx，－sinx，axlna，yu′·ux′，y对u，u对x，导数的运算方法等内容，欢迎下载使用。

(2)几何意义：函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y＝f(x)上点 处的 ．相应地，切线方程为 ．
y－f(x0)＝f′(x0)(x－x0)
3．基本初等函数的导数公式
f′(x)±g′(x)
f′(x)g(x)＋f(x)g′(x)
5．复合函数的导数复合函数y＝f(g(x))的导数和函数y＝f(u)，u＝g(x)的导数间的关系为yx′＝ ，即y对x的导数等于 的导数与 的导数的乘积．
• 温馨提醒 •二级结论1．奇函数的导数是偶函数，偶函数的导数是奇函数，周期函数的导数还是周期函数．2．函数y＝f(x)的导数f′(x)反映了函数f(x)的瞬时变化趋势，其正负号反映了变化的方向，其大小|f′(x)|反映了变化的快慢，|f′(x)|越大，曲线在这点处的切线越“陡”．
必明易错1．利用公式求导时要特别注意不要将幂函数的求导公式(xα)′＝αxα－1与指数函数的求导公式(ax)′＝axln a混淆．2．求曲线切线方程时，要分清在点P处的切线与过P点的切线的区别，前者只有一条，而后者包括了前者．3．曲线的切线与曲线的交点个数不一定只有一个，这和研究直线与二次曲线相切时有区别．　
1．函数y＝xcs x－sin x的导数为(　　)A．xsin x　　　　　　B．－xsin xC．xcs xD．－xcs x
题型二　导数的几何意义　　多维探究 导数的几何意义是每年高考的必考内容，考查题型既有选择题、填空题，也常出现在解答题的第(1)问中，难度偏小，属中、低档题．常见的命题角度有：(1)求切线方程；(2)求切点坐标；(3)求与切线有关的参数取值(范围).
考法(一)　求切线方程[例1]　(1)(2020·高考全国卷Ⅰ)曲线y＝ln x＋x＋1的一条切线的斜率为2，则该切线的方程为________．(2)已知函数f(x)＝xln x，若直线l过点(0，－1)，并且与曲线y＝f(x)相切，则直线l的方程为________．
[答案]　(1)2x－y＝0　(2)x－y－1＝0
　求曲线y＝f(x)的切线方程若已知曲线y＝f(x)过点P(x0，y0)，求曲线过点P的切线方程．(1)当点P(x0，y0)是切点时，切线方程为y－y0＝f′(x0)(x－x0)．(2)当点P(x0，y0)不是切点时，可分以下几步完成：第一步：设出切点坐标P′(x1，f(x1))；第二步：写出过点P′(x1，f(x1))的切线方程y－f(x1)＝f′(x1)(x－x1)；
第三步：将点P的坐标(x0，y0)代入切线方程求出x1；第四步：将x1的值代入方程y－f(x1)＝f′(x1)(x－x1)可得过点P(x0，y0)的切线方程．
考法(二)　求切点坐标[例2]　(2019·高考江苏卷)在平面直角坐标系xOy中，点A在曲线y＝ln x上，且该曲线在点A处的切线经过点(－e，－1)(e为自然对数的底数)，则点A的坐标是________．
考法(三)　求参数值或范围[例3]　(1)已知曲线y＝aex＋xln x在点(1，ae)处的切线方程为y＝2x＋b，则(　　)A．a＝e，b＝－1　　 B．a＝e，b＝1C．a＝e－1，b＝1 D．a＝e－1，b＝－1
3．若曲线C1：y＝ax2(a＞0)与曲线C2：y＝ex存在公共切线，则a的取值范围为________．
求解导数的几何意义与函数性质交汇问题的2个注意点(1)要注意函数相关性质在解题中的作用．(2)抓住导数的几何意义，利用函数性质或图象求解问题．