




2022届新高考数学人教版一轮课件:第七章 第四节 直线、平面平行的判定及其性质
展开知识点一 直线与平面平行直线与平面平行的判定定理和性质定理
l∥a,a⊂α,l⊄α
1.下列命题中正确的是( )A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a∥α,b⊄α,则b∥α
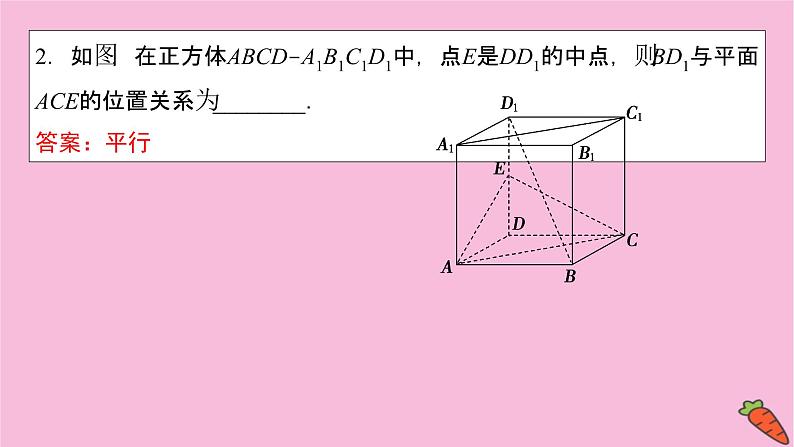
2.如图,在正方体ABCDA1B1C1D1中,点E是DD1的中点,则BD1与平面ACE的位置关系为________.答案:平行
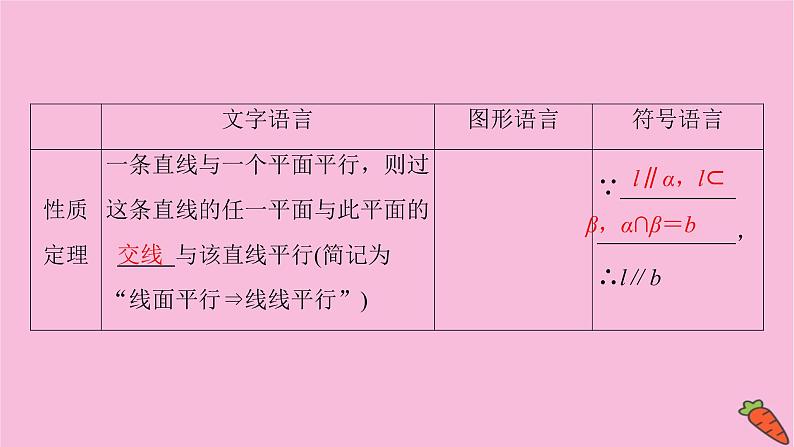
知识点二 平面与平面平行平面与平面平行的判定定理和性质定理
a∥β,b∥β,a∩b=P,a⊂α,b⊂α,
α∥β,α∩γ=a,β∩γ=b
• 温馨提醒 •平面与平面平行的几个有用性质(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(2)夹在两个平行平面之间的平行线段长度相等.(3)经过平面外一点有且只有一个平面与已知平面平行.(4)两条直线被三个平行平面所截,截得的对应线段成比例.(5)如果两个平面分别平行于第三个平面,那么这两个平面互相平行.(6)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.
1.平面α∥平面β的一个充分条件是( )A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α
2.若平面α∥平面β,直线a∥平面α,点B∈β,则在平面β内且过B点的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一的与a平行的直线
题型一 直线与平面平行的判定与性质 多维探究直线与平面平行的判定与性质是高考的考查重点.多考查直线与平面平行的判定、利用线面平行的性质判定线线平行及探索存在性问题.常见的命题角度有:(1)直线与平面平行的判定;(2)直线与平面平行的性质.
证明直线与平面平行的三种方法(1)定义法:一般用反证法.(2)判定定理法:关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言叙述证明过程.(3)性质判定法:即两平面平行时,其中一个平面内的任何直线都平行于另一个平面.
(1)证明:GH∥EF;(2)若EB=2,求四边形GEFH的面积.
[解析] (1)证明:因为BC∥平面GEFH,BC⊂平面PBC,且平面PBC∩平面GEFH=GH,所以GH∥BC.同理可证EF∥BC,因此GH∥EF.(2)连接AC,BD交于点O,BD交EF于点K,连接OP,GK.因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.又BD∩AC=O,且AC,BD都在底面ABCD内,所以PO⊥底面ABCD.又因为平面GEFH⊥平面ABCD,且PO⊄平面GEFH,
所以PO∥平面GEFH.因为平面PBD∩平面GEFH=GK,所以PO∥GK,所以GK⊥底面ABCD,从而GK⊥EF.所以GK是梯形GEFH的高.
证明线线平行的三种判定方法(1)利用平行公理.(2)利用线面平行的性质定理.(3)利用面面平行的性质定理.
[对点训练] 如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:GH∥平面PAD.
因为四边形ABCD是平行四边形,所以O是AC的中点.又M是PC的中点,所以AP∥OM.根据直线和平面平行的判定定理.则有PA∥平面BMD.因为平面PAHG∩平面BMD=GH,根据直线和平面平行的性质定理,得PA∥GH.因为GH⊄平面PAD,PA⊂平面PAD,所以GH∥平面PAD.
题型二 平面与平面平行的判定与性质 合作探究[例] 如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.
[证明] (1)因为G,H分别是A1B1,A1C1的中点,所以GH∥B1C1,又B1C1∥BC,所以GH∥BC,所以B,C,H,G四点共面.(2)在△ABC中,E,F分别为AB,AC的中点,所以EF∥BC,因为EF⊄平面BCHG,BC⊂平面BCHG,所以EF∥平面BCHG.又因为G,E分别为A1B1,AB的中点,
所以A1G綊EB,所以四边形A1EBG是平行四边形,所以A1E∥GB.因为A1E⊄平面BCHG,GB⊂平面BCHG,所以A1E∥平面BCHG.又因为A1E∩EF=E,所以平面EFA1∥平面BCHG.
[变式探究1] 在本例条件下,若D为BC1的中点, 求证:HD∥平面A1B1BA.证明:如图所示,连接HD,A1B,因为D为BC1的中点,H为A1C1的中点,所以HD∥A1B.又HD⊄平面A1B1BA,A1B⊂平面A1B1BA,所以HD∥平面A1B1BA.
[变式探究2] 在本例条件下,若D1,D分别为B1C1,BC的中点,求证:平面A1BD1∥平面AC1D.
判定面面平行的四种方法(1)面面平行的定义,即判断两个平面没有公共点.(2)面面平行的判定定理.(3)垂直于同一条直线的两平面平行.(4)平面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行.
[对点训练] 如图所示,平面α∥平面β,点A∈平面α,点C∈平面α,点B∈平面β,点D∈平面β,点E,F分别在线段AB,CD上,且AE∶EB=CF∶FD.
解析:(1)证明:①当AB,CD在同一平面内,∵α∥β,平面α∩平面ABDC=AC,平面β∩平面ABDC=BD,∴AC∥BD.∵AE∶EB=CF∶FD,∴EF∥BD.又EF⊄β,BD⊂β,∴EF∥平面β.
∵α∥β,α∩平面ACDH=AC,∴AC∥DH.故四边形ACDH是平行四边形.在AH上取一点G,使AG∶GH=CF∶FD,又∵AE∶EB=CF∶FD,∴GF∥HD,EG∥BH.又EG∩GF=G,∴平面EFG∥平面β.又EF⊂平面EFG,∴EF∥平面β.综上,EF∥平面β.
(2)如图所示,连接AD,取AD的中点M,连接ME,MF.∵E,F分别为AB,CD的中点,∴ME∥BD,MF∥AC,
直观想象、逻辑推理——直线与平面平行的创新应用[例] 如图所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCDA1B1C1D1中,AA1=2,AB=1,M,N分别在AD1,BC上移动,始终保持MN∥平面DCC1D1,设BN=x,MN=y,则函数y=f(x)的图象大致是( )
作平面MNQ∥平面DCC1D1,且由勾股定理得出y与x的关系是解题的关键.
[对点训练] 如图,透明塑料制成的长方体容器ABCDA1B1C1D1内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下面四个命题:
2024版新教材高考数学全程一轮总复习第七章立体几何第四节直线平面垂直的判定与性质课件: 这是一份2024版新教材高考数学全程一轮总复习第七章立体几何第四节直线平面垂直的判定与性质课件,共35页。PPT课件主要包含了必备知识·夯实双基,关键能力·题型突破,l⊥a,l⊥b,a⊂α,b⊂α,a∩b=O,a⊥α,b⊥α,直二面角等内容,欢迎下载使用。
高考数学(文数)一轮复习课件 第七章 立体几何 第四节 直线、平面平行的判定及其性质(含详解): 这是一份高考数学(文数)一轮复习课件 第七章 立体几何 第四节 直线、平面平行的判定及其性质(含详解),共26页。
高考数学文科总复习7.4直线、平面平行的判定及其性质课件PPT: 这是一份高考数学文科总复习7.4直线、平面平行的判定及其性质课件PPT,共53页。PPT课件主要包含了点击进入等内容,欢迎下载使用。












