





2022届新高考数学人教版一轮课件:第七章 第一节 空间几何体的结构特征
展开知识点一 简单几何体(1)简单旋转体的结构特征:①圆柱可以由 绕其任一边旋转得到;②圆锥可以由直角三角形绕其 旋转得到;③圆台可以由直角梯形绕 或等腰梯形绕 旋转得到,也可由 的平面截圆锥得到;④球可以由半圆或圆绕 旋转得到.
(2)简单多面体的结构特征:①棱柱的侧棱都 ,上下底面是 的多边形;②棱锥的底面是任意多边形,侧面是有一个 的三角形;③棱台可由 的平面截棱锥得到,其上下底面是 多边形.
1.下列说法正确的是( )A.棱柱的侧面都是矩形B.棱柱的侧棱都相等C.棱柱的棱都平行D.棱柱的侧棱总与底面垂直
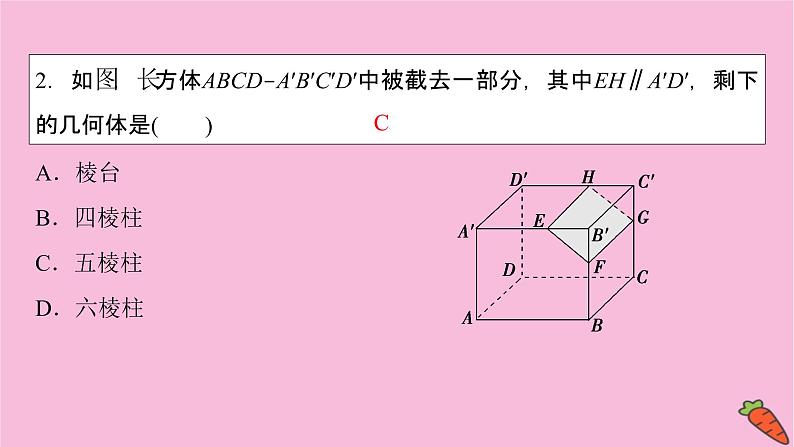
2.如图,长方体ABCDA′B′C′D′中被截去一部分,其中EH∥A′D′,剩下的几何体是( )
解析:根据题图①的底面为圆,侧面为扇形,得题图①折叠后的图形是圆锥;根据题图②的底面为三角形,侧面均为三角形,得题图②折叠后的图形是棱锥.
知识点二 直观图(1)画法:常用 .(2)规则:①原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为 ,z′轴与x′轴和y′轴所在平面 .②原图形中平行于坐标轴的线段,直观图中仍 .平行于x轴和z轴的线段在直观图中保持原长度 ,平行于y轴的线段长度在直观图中 .
1.下列说法正确的是( )A.相等的角在直观图中仍然相等B.相等的线段在直观图中仍然相等C.正方形的直观图是正方形D.若两条线段平行,则在直观图中对应的两条线段仍然平行
2.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为( )
题型一 空间几何体的结构特征 自主探究1.下列结论正确的是( )A.各个面都是三角形的几何体是三棱锥B.以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线
2.设有以下四个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体;④棱台的相对侧棱延长后必交于一点.其中真命题的序号是________.答案:①④
3.下列命题中错误的是________.①过球心的截面所截得的圆面的半径等于球的半径;②母线长相等的不同圆锥的轴截面的面积相等;③圆台所有平行于底面的截面都是圆面;④圆锥所有的轴截面都是全等的等腰三角形.解析:因为圆锥的母线长一定,根据三角形面积公式,当两条母线的夹角为90°时,圆锥的轴截面面积最大.答案:②
空间几何体概念辨析题的常用方法
题型二 空间几何体的直观图 自主探究1.如图所示为一个平面图形的直观图,则它的实际形状为( )A.平行四边形 B.梯形 C.菱形D.矩形
画几何体的直观图一般采用斜二测画法,其规则可以用“斜”(两坐标轴成45°或135°)和“二测”(平行于y轴的线段长度减半,平行于x轴和z轴的线段长度不变)来掌握.对直观图的考查有两个方向,一是已知原图形求直观图的相关量,二是已知直观图求原图形中的相关量.
直观想象——空间几何体的创新应用[例] (2021·八省联考模拟卷)北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的
(1)求四棱锥的总曲率;(2)若多面体满足:顶点数-棱数+面数=2,证明:这类多面体的总曲率是常数.
可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知:四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形.所以四棱锥的表面内角和由4个为三角形,1个为四边形组成,则其总曲率为:2π×5-(4π+2π)=4π.(2)证明:设顶点数、棱数、面数分别为n,l,m,所以有n-l+m=2.设第i个面的棱数为xi,所以x1+x2+…+xm=2l,
所以总曲率为:2πn-π[(x1-2)+(x2-2)+…+(xm-2)]=2πn-π(2l-2m)=2π(n-l+m)=4π,所以这类多面体的总曲率是常数.
通过直观想象,化空间图形为平面问题是求解此题的关键.
[对点训练] (2020·新高考全国卷Ⅰ)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面,在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
备战2024高考一轮复习数学(理) 第八章 立体几何 第一节 空间几何体的结构特征及表面积与体积课件PPT: 这是一份备战2024高考一轮复习数学(理) 第八章 立体几何 第一节 空间几何体的结构特征及表面积与体积课件PPT,共60页。PPT课件主要包含了多面体的结构特征,任一边,任一直角边,垂直于底边的腰,长对正,高平齐,宽相等,°或135°,平行于坐标轴,长度变为原来的一半等内容,欢迎下载使用。
高考数学一轮复习配套课件 第八章 第一节 空间几何体的结构特征及三视图和直观图: 这是一份高考数学一轮复习配套课件 第八章 第一节 空间几何体的结构特征及三视图和直观图,共53页。PPT课件主要包含了必备知识基础落实,关键能力考点突破,平行且相等,平行四边形,三角形,旋转体的结构特征,等腰三角形,等腰梯形,斜二测画法,平行于坐标轴等内容,欢迎下载使用。
高考数学(文数)一轮复习课件 第七章 立体几何 第一节 空间几何体的结构特征及三视图与直观图(含详解): 这是一份高考数学(文数)一轮复习课件 第七章 立体几何 第一节 空间几何体的结构特征及三视图与直观图(含详解)












