高中数学16.5二项式原理说课ppt课件

这是一份高中数学16.5二项式原理说课ppt课件，共14页。PPT课件主要包含了项数次数+1，定理的证明等内容，欢迎下载使用。
( a + b ) 2 =
思考:(a+b)4的展开式是什么?
( a + b ) 3 =
次数:各项的次数等于二项式的次数
(a+b)2＝ (a+b) (a+b)
展开后其项的形式为：a2 ， ab ， b2
这三项的系数为各项在展开式中出现的次数。考虑b
恰有1个取b的情况有C21种，则ab前的系数为C21
恰有2个取b的情况有C22 种，则b2前的系数为C22
每个都不取b的情况有1种，即C20 ,则a2前的系数为C20
对(a+b)2展开式的分析
(a+b)4＝ (a+b) (a+b) (a+b) (a+b)＝？
问题：1)．(a+b)4展开后各项形式分别是什么？
2)．各项前的系数代表着什么？
3)．你能分析说明各项前的系数吗？
a4 a3b a2b2 ab3 b4
各项前的系数 代表着这些项在展开式中出现的次数
每个都不取b的情况有1种，即C40 ,则a4前的系数为C40
恰有1个取b的情况有C41种，则a3b前的系数为C41
恰有2个取b的情况有C42 种，则a2b2前的系数为C42
恰有3个取b的情况有C43 种，则ab3前的系数为C43
恰有4个取b的情况有C44种，则b4前的系数为C44
则 (a+b)4 ＝ C40 a4 ＋C41 a3b ＋C42 a2b2 ＋C43 ab3 ＋C44 b4
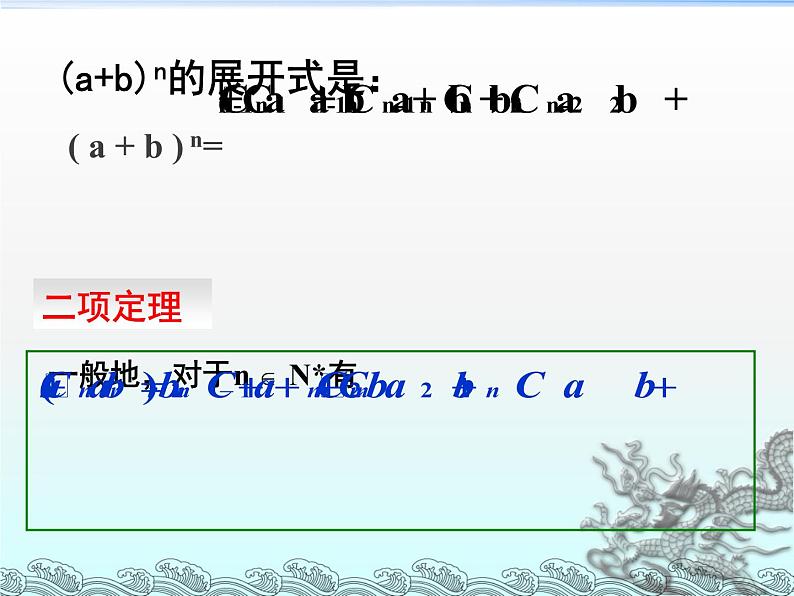
( a + b ) n=
(a+b)n的展开式是：
(a+b)n是n个(a+b)相乘，
每个（a+b）在相乘时有两种选择，选a或b. 而且每个(a+b)中的a或b选定后才能得到展开式的一项。
对于每一项akbn-k，它是由k个(a+b)选了a，n-k个(a+b)选了b得到的，它出现的次数相当于从n个(a+b)中取k个a的组合数，将它们合并同类项，就得二项展开式，这就是二项式定理。
其中每一项都是akbn-k的形式，k=0，1，…，n；
二项式定理： n ∈ N *
注:(1) 上式右边为二项展开式, 各项次数都等于二项式的次数
(2) 展开式的项数为 n+1 项；
(3) 字母a按降幂排列,次数由n递减到0 字母b按升幂排列,次数由0递增到n
(4)二项式系数可写成组合数的形式, 组合数的下标为二项式的次数 组合数的上标由0递增到n
(5) 展开式中的第 r + 1 项，即通项 Tr+1 =__________；
(6) 二项式系数为 ______；
项的系数为 二项式系数与数字系数的积
在二项式定理中，令a=1，b=x，则有：
在上式中，令 x = 1，则有：
3、求(x+a)12的展开式中的倒数第4项。
4、(1)求(1+2x)7的展开式中第4项的系数。