初中数学北师大版八年级下册4 简单的图案设计优秀精练
展开
3.4简单的图案设计同步练习北师大版初中数学八年级下册
一、选择题(本大题共12小题,共36.0分)
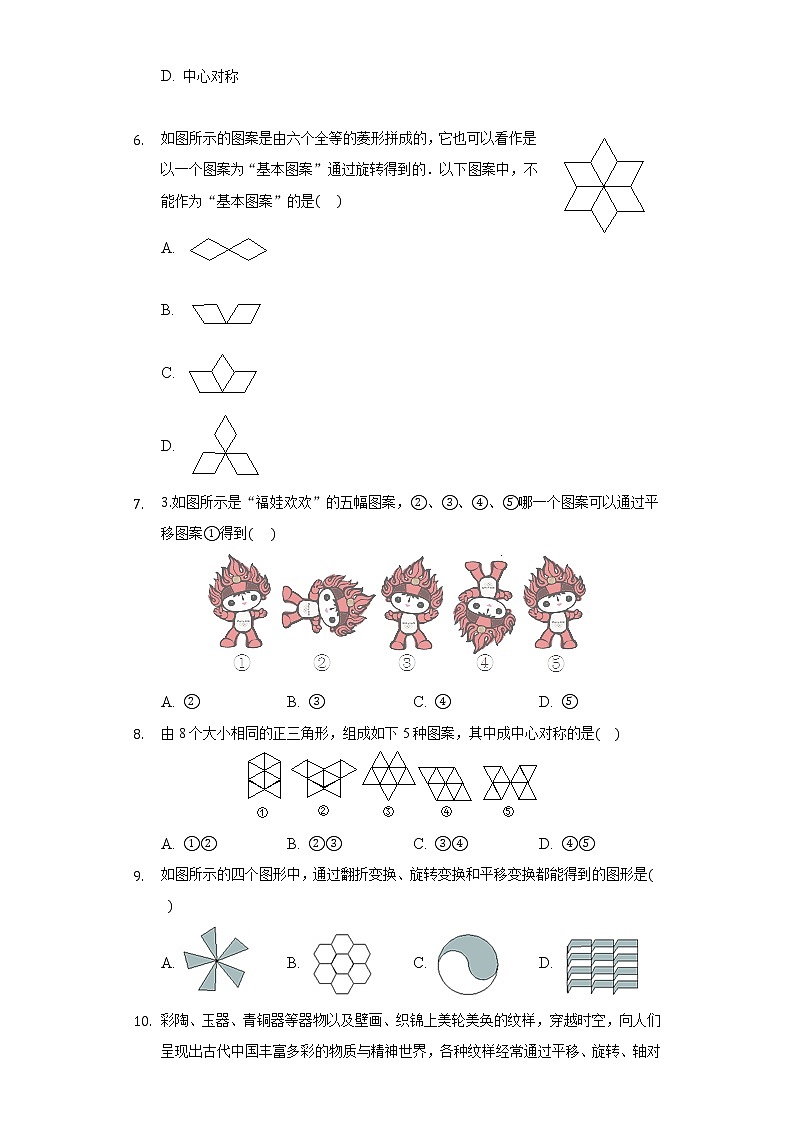
- 下面由四个相同正方形拼成的图形中,是中心对称图形但不是轴对称图形的是
A. B. C. D.
- 如图,下列四个图形都可以分别看成由一个“基本图案”经过旋转所形成,则它们中旋转角相同的图形为
A. B. C. D.
- 下列图形中,可以由原图旋转得到的是
A. B. C. D.
- 如图所示的图案是由下列哪个图形旋转得到的
A.
B.
C.
D.
- 经过下列变换,不能由图所示的基本图形得到图的是
A. 旋转和平移
B. 中心对称和轴对称
C. 平移和轴对称
D. 中心对称
- 如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”通过旋转得到的.以下图案中,不能作为“基本图案”的是
A.
B.
C.
D.
- 如图所示是“福娃欢欢”的五幅图案,、、、哪一个图案可以通过平移图案得到
A. B. C. D.
- 由8个大小相同的正三角形,组成如下5种图案,其中成中心对称的是
A. B. C. D.
- 如图所示的四个图形中,通过翻折变换、旋转变换和平移变换都能得到的图形是
A. B. C. D.
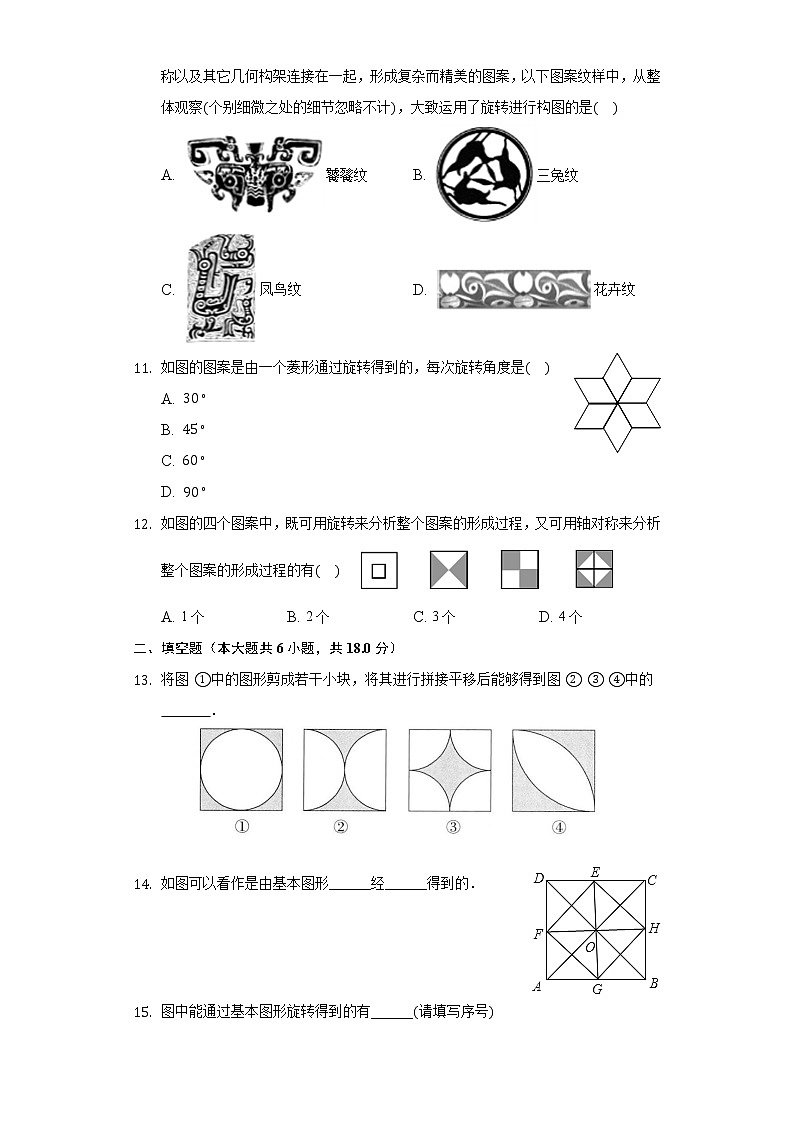
- 彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样,穿越时空,向人们呈现出古代中国丰富多彩的物质与精神世界,各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起,形成复杂而精美的图案,以下图案纹样中,从整体观察个别细微之处的细节忽略不计,大致运用了旋转进行构图的是
A. 饕餮纹 B. 三兔纹
C. 凤鸟纹 D. 花卉纹
- 如图的图案是由一个菱形通过旋转得到的,每次旋转角度是
A.
B.
C.
D.
- 如图的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的有
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题共6小题,共18.0分)
- 将图中的图形剪成若干小块,将其进行拼接平移后能够得到图中的 .
- 如图可以看作是由基本图形______经______得到的.
|
- 图中能通过基本图形旋转得到的有______请填写序号
- 如图,在平面直角坐标系xOy中,可以看作是经过若干次图形的变化平移、轴对称、旋转得到的,写出一种由得到的过程:_____.
- 如图,在正方形网格中,线段可以看作是线段AB经过若干次图形的变化平移、旋转、轴对称得到的,写出一种由线段AB得到线段的过程______
|
- 在下列图案中可以用旋转得到的是______填序号.
三、解答题(本大题共7小题,共56.0分)
- 如图1,图2,图3的网格均由边长为1的小正方形组成,图1中的团是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.
图1中的“弦图”的四个直角三角形组成的图形是______对称图形填“轴”或“中心”.
请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
图2中所设计的图案不含方格纸必须是轴对称图形而不是中心对称图形,图3中所设计的图案不含方格纸必须既是轴对称图形,又是中心对称图形.
- 如图所示,在的方格内,已将其中的2个小正方形涂成黑色,请你分别在图、图、图、图中再将两个空白的小正方形涂成黑色,使4个黑色小正方形组成一个轴对称图形,画出与示意图不同的4种方案.每个的方格内限画一种
要求:个黑色小正方形必须相连;有公共边或公共顶点视为相连
将选中的小正方形方格用黑色签字笔涂成阴影图形.若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案
- 如图,由5个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,使每个小正方形的顶点仍为格点,请在图,图,图中分别画出满足以下各要求的图形.
使得图形既是轴对称图形,又是中心对称图形;
使得图形成为轴对称图形,而不是中心对称图形;
使得图形成为中心对称图形,而不是轴对称图形.
- 七巧板又称智慧板,是中国民间流传的智力玩具,它是由七块板组成如图,用这七块板可拼出许多图形种以上,例如:三角形、平行四边形、以及不规则的多边形,它还可以拼出各种人物、动物、建筑等.请你用七巧板中标号为的三块板如图2经过平移、旋转拼出下列图形相邻两块板之间无空隙,无重叠;示意图的顶点画在小方块顶点上:
拼成长方形,在图3中画出示意图;
拼成等腰直角三角形,在图4中画出示意图.
- 如图,机械手要将一个工件从图中的A处移动到B处,但是这个工件不能碰到图中的障碍不包括坐标轴所表示的蓝线,试用坐标写出一条机械手在移动中可能要经过的路线机械手的行走路线均经过格点.
- 在图中的空白正方形内部设计一个图案,使得设计的图案和正方形构成的整体是一个既中心对称又轴对称的图案,并说明你所设计图案的含义.
|
- 在平面直角坐标系中,将坐标为,,,的点用线段依次连接起来得到一个图案N
将图案N向左平移3个单位长度,画出平移后的图案;
将图案N向下平移4个单位长度,画出平移后的图案;
将图案N先向左平移3个单位长度,再向下平移4个单位长度,画出第二次平移后的图案;
画出图案N关于横轴对称的图案;
画出图案N关于纵轴对称的图案;
以原点为对称中心,画出与图案N成中心对称的图案.
答案和解析
1.【答案】D
【解析】解:根据中心对称图形的概念与轴对称图形的概念可知:
A、既是中心对称图形又是轴对称图形;
B、是轴对称图形但不是中心对称图形;
C、既是中心对称图形又是轴对称图形;
D、是中心对称图形但不是轴对称图形;
故选:D.
根据中心对称图形的定义旋转后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.
此题主要考查了中心对称图形与轴对称图形的定义,根据定义得出图形形状是解决问题的关键.
2.【答案】D
【解析】
【分析】
本题考查了利用旋转设计图案,根据图形求出旋转角是解题的关键,根据图形,分别求出各图形的旋转角,然后即可得解.利用正方形的定义找出旋转中心,把周角分成四个相等的角是求旋转角的关键,也是本题的难点.
【解答】
旋转角为,
旋转角为,
如图,找出旋转中心,根据正方形的定义分成四个相等的角,
旋转角为,
旋转角为,
所以,的旋转角都是,相同.
故选:D.
3.【答案】B
【解析】解:A、可以由原图轴对称得到,不合题意;
B、可以由原图旋转得到,符合题意;
C、可以由原图轴对称得到,不合题意;
D、可以由原图轴对称得到,不合题意.
故选:B.
旋转是围绕一点旋转一定的角度的图形变换,因而旋转一定有旋转中心和旋转角,且旋转前后图形能够重合,这是判断旋转的关键,据此解答即可.
此题主要考查了利用旋转设计图案,通过旋转变换不同角度或者绕着不同的旋转中心向着不同的方向进行旋转都可设计出美丽的图案.
4.【答案】D
【解析】解:由图可得,如图所示的图案是由绕着一端旋转3次,每次旋转得到的,
故选:D.
由一个基本图案可以通过旋转等方法变换出一些复合图案.
本题主要考查了利用旋转变换设计图案,关键是利用旋转中的三个要素旋转中心;旋转方向;旋转角度设计图案.通过旋转变换不同角度或者绕着不同的旋转中心向着不同的方向进行旋转都可设计出美丽的图案.
5.【答案】D
【解析】解:因为经过旋转和平移能由图所示的基本图形得到图,所以A选项不符合题意;
因为经过中心对称和轴对称能由图所示的基本图形得到图,所以B选项不符合题意;
因为经过平移和轴对称能由图所示的基本图形得到图,所以C选项不符合题意;
因为经过中心对称不能由图所示的基本图形得到图,所以D选项符合题意.
故选:D.
根据旋转、平移、轴对称、中心对称的性质即可进行逐一判断.
本题考查了利用旋转、平移、轴对称、中心对称设计图案,解决本题的关键是掌握旋转、平移、轴对称、中心对称的性质.
6.【答案】B
【解析】
【分析】
本题考查了图形的旋转变化,难度不大,但易错,认真观察旋转得到的图案,找到旋转中心,即可判断.
【解答】
解:顺时针,连续旋转60度,三次即可得到;
B.不能作为“基本图案”;
C.旋转180度,即可得到;
D.旋转60度即可;
故选B.
7.【答案】D
【解析】A选项:是由旋转得到,故错误;
B选项:是由轴对称得到,故错误;
C选项:是由旋转得到,故错误;
D选项:形状和大小没有变化,由平移得到,故正确.
故选 D.
8.【答案】D
【解析】
【分析】
本题主要考查中心对称的定义,可以根据中心对称的定义:“如果一个图形绕着一个点旋转,能够与自身完全重合,这个图形是中心对称图形”,对三角形形成的图案进行分析,确定符合定义的图案即可.
【解答】
解:根据轴对称图形的定义,图案是轴对称图形,
根据中心对称图形的定义,可知图案是中心对称图形.
故选D.
9.【答案】B
【解析】
【分析】
本题考核知识点:图形的翻折变换、旋转变换和平移变换.解题关键点:理解图形的变换概念.
根据翻折变换、旋转变换和平移变换的定义进行分析即可.
【解答】
解:选项A只能旋转得到;选项B通过翻折变换、旋转变换和平移变换都能得到;选项C只能旋转得到;选项D只能平移得到,
故选:B
10.【答案】B
【解析】
【分析】
根据旋转的性质与特点判断即可.
此题考查旋转问题,关键是根据旋转、对称、平移、位似的特点解答.
【解答】
解:A、图中利用的是对称,错误;
B、图中利用的是旋转,正确;
C、图中利用的位似,错误;
D、图中利用的是平移,错误;
故选:B.
11.【答案】C
【解析】
【分析】
此题主要考查了利用旋转设计图案,菱形的性质,6个相等的角构成一个周角,每一个角一定为根据所给出的图,6个角正好构成一个周角,且6个角都相等,则每次旋转.
【解答】
解:设每次旋转角度,
则,解得,
每次旋转角度是.
故选C.
12.【答案】D
【解析】
【分析】
考查了旋转和轴对称的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心;轴对称图形的对应线段、对应角相等.根据旋转、轴对称的定义来分析.图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动;轴对称是指如果一个图形沿一条直线折叠,直线两侧的图形能够互相重合,就是轴对称.
【解答】
解:图形1可以旋转得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形2可以旋转得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形3可以旋转得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形4可以旋转得到,也可以经过轴对称,沿一条直线对折,能够完全重合.
故既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有4个.
故选D.
13.【答案】
【解析】解:将题图中的图形剪成若干块,通过拼接平移能得到,不能拼成.
14.【答案】正方形AGOF 绕点O旋转
【解析】解:根据旋转的意义,正方形AGOF围绕O点顺时针旋转可得到正方形OFDE,再旋转,可得到正方形OECH,因此可以看作是由基本图形正方形AGOF经绕点O旋转得到的.
观察图形,根据旋转的意义,可以看出图形是如何得到的.
本题考查了图形的旋转变化,学生主要要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错.
15.【答案】
【解析】解:四幅图中,能通过基本图形旋转得到的有:.
故答案为:.
观察图形是否有几个相同的部分共同组成,即可作出判断.
本题主要考查了几何图形的变换,关键在于认真分析图形,找到各图形的组成部分.
16.【答案】将沿x轴向下翻折,在沿x轴向左平移2个单位长度得到
【解析】【解析】
分析:根据旋转的性质、轴对称的性质、平移的性质、即可得到由ABO得到OCD的过程.
详解:将ABO沿x轴向下翻折,再沿x轴向左平移2个单位长度得到OCD答案不唯一.
故答案为将ABO沿x轴向下翻折,再沿x轴向左平移2个单位长度得到OCD.
点睛:本题考查了坐标与图形变化旋转、对称与平移观察得出由ABO得到OCD的过程是解题的关键.
17.【答案】将线段AB绕点B逆时针旋转,在向右平移2个单位长度
【解析】解:线段可以看作是由线段AB绕B点顺时针旋转,并向右平移2个单位得到线段.
故答案为:将线段AB绕点B逆时针旋转,在向右平移2个单位长度
根据旋转的性质,平移的性质即可解决问题;
考查了坐标与图形变化旋转,平移,对称,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
18.【答案】
【解析】
【分析】
通过旋转变换不同角度或者绕着不同的旋转中心向着不同的方向进行旋转都可设计出美丽的图案,进而判断得出即可.
【详解】
通过旋转得到;是通过平移得到.故答案为:.
【点睛】
本题是考查了运用旋转设计图案,根据旋转图形的特点得出是解题关键.
19.【答案】中心
【解析】解:图1中的“弦图”的四个直角三角形组成的图形是中心对称图形.
如图2是轴对称图形而不是中心对称图形;图3既是轴对称图形,又是中心对称图形.
利用中心对称图形的意义得出答案即可;
每个直角三角形的顶点均在方格纸的格点上,且四个三角形不重叠,是轴对称图形;
所设计的图案不含方格纸必须是中心对称图形或轴对称图形画出图.
本题考查利用旋转或者轴对称设计方案,关键是理解旋转和轴对称的概念,按照要求作出图形即可.
20.【答案】解:如图所示:
.
【解析】利用轴对称图形的性质以及旋转的性质、平移的性质分别得出符合题意的答案.
此题主要考查了利用旋转设计图案,正确掌握相关图形性质是解题关键.
21.【答案】解:如图所示:
;
如图所示:
;
如图所示:
.
【解析】本题是图案设计问题,用轴对称和中心对称知识画图,设计图案,要按照题目要求,展开丰富的想象力,答案不唯一.本题是图案设计问题,由于设计方案的多样化,只要满足相应问题对轴对称,中心对称的要求即可,这样就可以发挥学生丰富的想象力,提高学习兴趣.
根据轴对称图形和中心对称图形的定义设计图案即可;
根据轴对称图形和中心对称图形的定义设计图案即可;
根据轴对称图形和中心对称图形的定义设计图案即可.
22.【答案】解:如图3中,长方形即为所求答案不唯一.
如图4中,等腰直角三角形即为所求.
【解析】根据长方形的定义,利用平移,性质,翻折等知识,画出图形即可.
根据等腰直角三角形的定义,利用平移,性质,翻折等知识,画出图形即可.
本题考查利用旋转设计图案,等腰直角三角形,长方形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
23.【答案】解:如图所示:A先向左平移2个单位,再向上平移9个单位,再向右平移3个单位,再向下平移2个单位,即可得出B点位置,如图中红线所示.坐标变化为.
【解析】利用已知图形得出A点移动的路径即可.
此题主要考查了平移设计图案,利用网格结合题意得出运动路径是解题关键.
24.【答案】解:图案如图所示:
代表一个风车.
【解析】根据轴对称图形,中心对称图形的定义画出图形即可答案不唯一.
本题考查利用旋转设计图案,利用轴对称设计图案,属于中考常考题型.
25.【答案】解:将图案N向左平移3个单位长度,平移后的图案如图1所示.
将图案N向下平移4个单位长度,平移后的图案如图2所示.
将图案N先向左平移3个单位长度,再向下平移4个单位长度,第二次平移后的图案如图3所示.
图案N关于横轴对称的图案如图4所示.
图案N关于纵轴对称的图案如图5所示.
以原点为对称中心,与图案N成中心对称的图案如图6所示.
【解析】把所有的点左平移3个单位长度即可.
把所有的点向下平移4个单位长度即可.
把所有的点向左平移3个单位长度,再向下平移4个单位长度即可.
画出所有的点关于x轴的对称点即可.
画出所有的点关于y轴的对称点即可.
画出所有的点关于原点的对称点即可.
本题考查利用平移、旋转、轴对称设计图案,解题的关键是理解平移、旋转、轴对称的定义,属于中考作图题目中常考题型.
数学八年级下册4 简单的图案设计习题: 这是一份数学八年级下册4 简单的图案设计习题,共9页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
北师大版八年级下册4 简单的图案设计精练: 这是一份北师大版八年级下册4 简单的图案设计精练,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北师大版八年级下册第三章 图形的平移与旋转4 简单的图案设计习题: 这是一份北师大版八年级下册第三章 图形的平移与旋转4 简单的图案设计习题,共7页。试卷主要包含了故答案为4等内容,欢迎下载使用。