初中数学北师大版七年级下册第三章 变量之间的关系2 用关系式表示的变量间关系优秀练习题

这是一份初中数学北师大版七年级下册第三章 变量之间的关系2 用关系式表示的变量间关系优秀练习题，共15页。试卷主要包含了2用关系式表示的变量间关系，0分），12x B，1米．，【答案】C，【答案】A等内容，欢迎下载使用。
 3.2用关系式表示的变量间关系一、选择题（本大题共12小题，共36.0分）某油箱容量为60L的汽车，加满汽油行驶了100km时，油箱中的汽油大约消耗了，如果加满汽油后汽车行驶的路程为xkm，油箱中剩油量为yL，则y与x之间的关系式和自变量的取值范围分别是    A.  B.
C.  D. 某汽车油箱中盛有油100L，装满货物行驶的过程中每小时耗油8L，则油箱中的剩油量与时间之间的关系式是A.  B.  C.  D. 在地球某地，地表以下岩层的温度与所处深度之间的关系可以近似地用表达式来表示，当自变量x每增加1km时，因变量y的变化情况是A. 减少 B. 增加 C. 减少 D. 增加变量x与y之间的关系是，当时，自变量x的值是A. 13 B. 5 C. 2 D. 小颖现已存款200元，为赞助“希望工程”，她计划今后每月存款10元，则存款总金额元与时间月之间的关系式是A.  B.  C.  D. 一名老师带领x名学生到动物园参观，已知成人票每张30元，学生票每张10元．设门票的总费用为y元，则y与x的关系为    A.  B.  C.  D. 在关系式中，当自变量时，因变量y的值为    A. 7 B. 14 C. 17 D. 21我国是水资源比较贫乏的国家，所以各省市都采取了各项措施加强公民的节水意识某市规定了如下的用水收费标准：每户每月的用水不超过10立方米时，水费按每立方米元收费，超过10立方米时，不超过的部分仍按每立方米元收费，超出部分按每立方米3元收费设该市某户7月份用水量为立方米，应交水费为元用水不超过10立方米时与超过10立方米时，y与x之间的关系式是    A. 当时，当时，
B. 当时，当时，
C. 当时，当时，
D. 当时，当时，从A地向B地打长途电话，通话3分钟以内收费元，3分钟后通话时间每增加1分钟加收1元．若通话时间为单位：分，，且x为整数，则通话费用单位：元与通话时间单位：分的关系式是    A.  B.  C.  D. 如图所示，在长方形ABCD中，，，P是CD上的动点，且不与点C，D重合，设，梯形ABCP的面积为y，则y与x之间的关系式和自变量的取值范围分别是A. ； B. ；
C. ； D. ；如图所示，在中，已知，高线，动点由点C沿CB向点B移动不与点B重合设的长为x，的面积为S，则S关于x的关系式为     A.  B.  C.  D. 用100元钱在网上书店恰好可购买m本书，但是每本书需另加邮寄费6角，购买n本书共需费用y元，则可列出关系式A.  B.
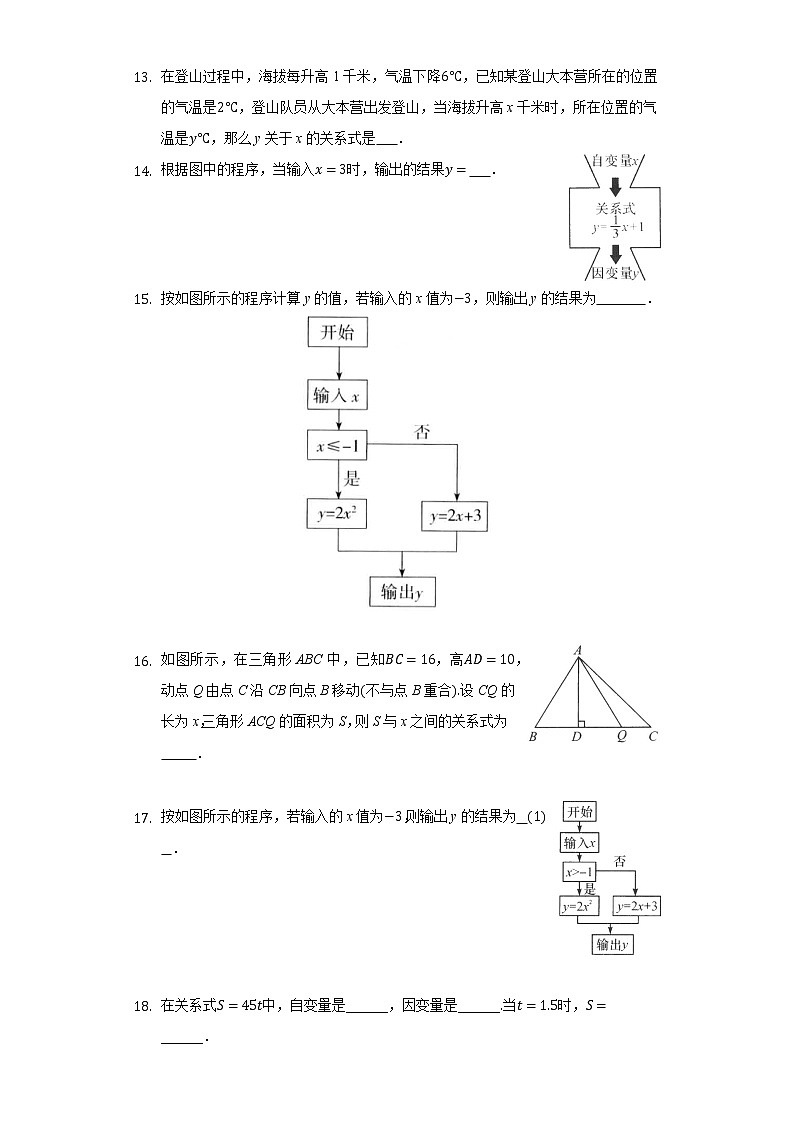
C.  D. 二、填空题（本大题共7小题，共21.0分）在登山过程中，海拔每升高1千米，气温下降，已知某登山大本营所在的位置的气温是，登山队员从大本营出发登山，当海拔升高x千米时，所在位置的气温是，那么y关于x的关系式是      ．根据图中的程序，当输入时，输出的结果      ．


  按如图所示的程序计算y的值，若输入的x值为，则输出y的结果为              ．
如图所示，在三角形ABC中，已知，高，动点Q由点C沿CB向点B移动不与点B重合设CQ的长为x，三角形ACQ的面积为S，则S与x之间的关系式为          ．
  按如图所示的程序，若输入的x值为，则输出y的结果为      ．



  在关系式中，自变量是______，因变量是______当时，______．为了解某品牌汽车的耗油量，人们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成下表：汽车行驶时间0123油箱剩余油量100948882根据上表的数据，写出Q与t的关系式：                 ．三、解答题（本大题共6小题，共48.0分）将若干张长、宽的长方形白纸按下图所示的方法粘合起来．粘合部分的宽为．
 求4张白纸粘合后的总长度．设x张白纸粘合后的总长度为，写出y与x的关系式．






 长方形的一边长是16，其邻边长为x，周长是y，面积为S．写出x和y之间的关系式写出x和S之间的关系式当时，x等于多少等于多少当x增加2时，y增加多少增加多少






 将长为、宽为的长方形白纸，按如图所示的方法黏合起来，黏合部分宽为．根据图，将表格补充完整：白纸张数12345纸条长度40 110145 设x张白纸黏合后的总长度为，则y与x之间的关系式是什么？你认为白纸黏合起来总长度可能为吗？为什么？






 “十一”期间，小明和父母一起开车到距家的景点旅游，出发前，汽车油箱内储油，当行驶时，发现油箱余油量为假设行驶过程中汽车的耗油量是均匀的．求该车平均每千米的耗油量，并写出行驶路程与剩余油量的关系式；当时，求剩余油量Q．






 有一棵树苗，刚栽下去时树高为米，以后每年长米．写出树高米与年数年之间的关系式：________；年后的树高为________米；________年后树苗的高度将达到米．






 多边形的内角和随着边数的变化而变化．设多边形的边数为n，内角和为，则变量N与n之间的关系可以表示为．在这个关系式中，自变量、因变量各是什么？在这个关系式中，n能取什么样的值？利用这个关系式计算六边形的内角和；当边数每增加1时，多边形的内角和如何变化？







答案和解析1.【答案】D
 【解析】【分析】
此题主要考查了用关系式表示变量间的关系，求出每千米汽车的耗油量是解题关键．
首先求出汽车每千米耗油量，进而得出y与x之间的关系式．
【解答】
解：由题意得，每千米汽车的耗油量为：，
则油箱中剩余油量．
由已知得汽车的行驶路程最远为：，
故自变量的取值范围为．
所以．
故选D．  2.【答案】C
 【解析】【分析】
根据油箱剩油量等于总油量减去消耗的油量列出关系式即可．
本题考查了用关系式表示变量间的关系，比较简单．
【解答】
解：由题意得，油箱剩油量．
故选C．  3.【答案】B
 【解析】【分析】
本题考查用关系式表示的变量间关系，弄清关系式中自变量和因变量的关系是解题关键．根据关系式解答即可．
【解答】
解：由可知，
当自变量x每增加1km时，因变量，
所以，即因变量y增加．
故选B．  4.【答案】C
 【解析】【分析】
此题主要考查变量x与y之间的关系式，关键是掌握已知的关系式，给出因变量的值时，解方程求出相应的自变量的值即可．
直接把代入，解方程即可．
【解答】
解：当时，，
解得：．
故选C．  5.【答案】D
 【解析】分析
本题考查用关系式表示的变量间关系，解答本题的关键是明确题意，找出其中自变量和因变量间的关系式．
根据题意可以写出存款总金额元与时间月之间的关系式，从而可以解答本题．
详解
解：由题意可得：．
故选D．
 6.【答案】D
 【解析】分析
本题考查了用关系式表示变量间的关系，关键是理解学生的票价加老师的票价等于总票价．根据学生人数乘以学生票价，老师人数乘以成人票价，相加可得总费用，代入数值即可得关系式．
详解
解：由题意得x名学生和1名老师的总费用为：
．
故选D．
 7.【答案】C
 【解析】略
 8.【答案】D
 【解析】解：当时，
当时，．
故选D．
 9.【答案】A
 【解析】【分析】
本题考查了用关系式表示变量间的关系，仔细审题得出变量与变量的关系是解题关键．
根据通话总费用超过3分钟后的超出费用，即可列出y与x的关系式．
【解答】
解：因为通话时间不超过3分钟收费均为元，超过3分钟后，每分钟收取1元，且x为整数，
故可得通话费用单位：元与通话时间单位：分的关系式：．
故选A．  10.【答案】A
 【解析】分析
本题考查了用关系式表示变量间的关系、自变量取值范围及梯形面积先确定梯形ABCP的上底、下底和高，代入数据即可得梯形ABCP的面积y与DP长x之间的关系式．
详解
解：由梯形面积公式知，，，，
，
即，
且不与点C，D重合
，
．
故选A．
 11.【答案】A
 【解析】分析
此题考查了用关系式表示变量间的关系，关键是利用三角形面积公式列出关系式．
设的长为x，得出的长为，再根据三角形的面积公式列出关系式即可．
详解
解：设的长为x，可得的长为，
所以S与x之间的关系式为．
故选A．
 12.【答案】A
 【解析】分析
此题考查用关系式表示变量之间的关系，用100元钱购买m本书即可计算平均每本书的价格，再根据费用平均每本书价格邮费，即可列出关系式．
详解
解：由题意得，平均每本书价格为，
购买n本书共需费用．
故选A．
 13.【答案】
 【解析】略
 14.【答案】2
 【解析】略
 15.【答案】18
 【解析】解：，把代入，得，故答案为18．
 16.【答案】
 【解析】【分析】
本题考查了函数关系式，利用三角形的面积是解题关键．根据三角形的面积公式，可得答案．
【解答】
解：，，
，
故答案为．  17.【答案】
 【解析】略
 18.【答案】t；S；．
 【解析】【分析】
本题考查了函数关系式的知识，要求能由函数关系式及一个变量的值求另一个变量的值．根据关系式可判断自变量是t，因变量是S，由t的值，可确定S的值．
【解答】
解：关系式中，自变量是t，因变量是S．
当时，
故答案为t；S；．  19.【答案】
 【解析】解：由表格可知，开始油箱中的油为，每行驶1小时，油量减少，与t的关系式为，故答案为．
 20.【答案】解：张白纸粘合后的总长度；
由题意得：．
 【解析】此题考查变量之间的应用，注意观察图意，找出规律解决问题．
根据白纸粘合后的总长度张白纸的长个粘合部分的宽即可；
根据白纸粘合后的总长度张白纸的长个粘合部分的宽，列出关系式即可．
 21.【答案】解：由长方形的周长公式，得．由长方形的面积公式，得．当时，，．当x增加2时，y增加4，S增加32．
 【解析】略
 22.【答案】解：  180 
．
不可能．
理由：令，
解得．
因为x为整数，
所以总长度不可能为．
 【解析】略
 23.【答案】解：
该车平均每千米的耗油量为，
行驶路程与剩余油量的关系式为．
当时，．
故当时，剩余油量Q为．
 【解析】略
本题考查了变量之间的关系，属于基础题．
求出该车平均每千米的耗油量，即可列出行驶路程与剩余油量Q的关系式；
根据中所求关系式计算即可．
 24.【答案】   
 【解析】略
 25.【答案】解：是自变量，N是因变量．
取大于2的整数．
当时，，故六边形的内角和为．
当边数每增加1时，多边形的内角和增加．
 【解析】略