






华师大版八年级上册2 等腰三角形的判定教学ppt课件
展开在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
我们知道,如果一个三角形有两条边相等,那么它们所对的角相等,反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
画画看,你发现了什么?
已知:在△ABC中,∠B=∠C(如图).求证:AB=AC.
想想看,还可以添加什么辅助线证明这一结论?
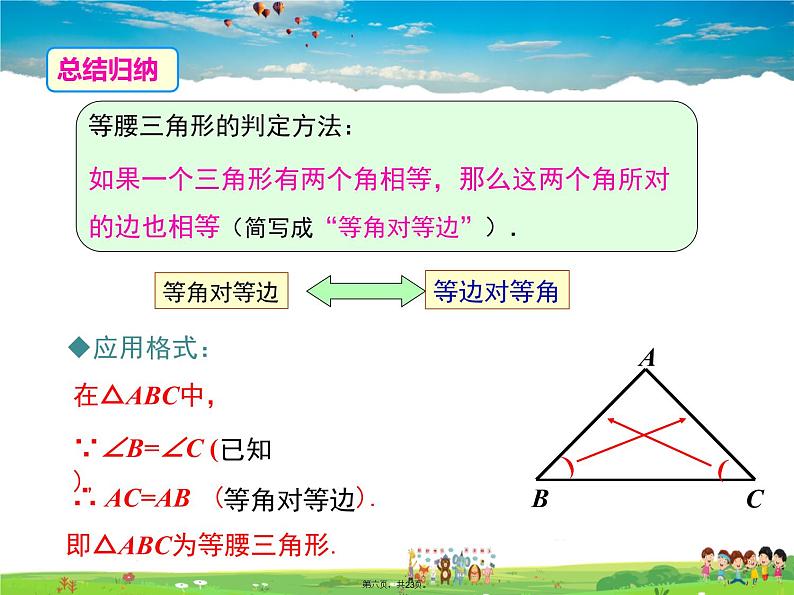
等腰三角形的判定方法: 如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
例1 如图,在△ABC中,已知∠A=40°,∠B=70°.求证:AB=AC.
证明:∵∠A+∠B+∠C=180°(三角形的内角和等于180°), ∠A=40°,∠B=70°(已知), ∴∠C=180°-∠A-∠B(等式的性质), =180°-40°-70°=70°, ∴∠C=∠B(等量代换), ∴AB=AC.
例2 如图,AB∥CD, ∠1=∠2,求证:AB=AC.
证明:∵ AB∥CD (已知),∴ ∠B= ∠2 (两直线平行,同位角相等).又∵ ∠1=∠2,∴ ∠B= ∠1(等量代换).∴ AB=AC(等角对等边).
一个三角形满足什么条件就是等边三角形?
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1.三个角都相等的三角形是等边三角形;2.有一个角等于60°的等腰三角形是等边三角形.
三个角都相等的三角形是等边三角形.
已知:如图,∠A= ∠ B=∠C.求证: AB=AC=BC.
判定2:有一个角是60°的等腰三角形是等边三角形
已知: 若AB=AC , ∠A= 60°.求证: AB=AC=BC.
动动手 若AB=AC , ∠B= 60°,求证AB=AC=BC.
例3 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
变式:上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
如图,在等边三角形ABC中,AD=AE, 求证:△ADE是等边三角形.
例4 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
求证:△ABC是等腰三角形.
已知:如图,∠CAE是△ABC的外角,AD平分∠CAE , AD∥BC.
证明:∵AD∥BC(已知),∴∠1=∠B(两直线平行,同位角相等) ∠2=∠C(两直线平行,内错角相等)∵ AD平分∠CAE, ∴ ∠1=∠2.∴∠B=∠C.∴ △ABC是等腰三角形.
∵ ∠ACB= ∠ A'C'B'=90°(已知),∴ ∠BC'B'= ∠ACB+∠ A'C'B'=180°.即点B、C'、B' 在同一条直线上.在△A'B'B中,AB= A'B'(已知),∴ ∠B= ∠B'(等角对等边).在△ABC和 △A'B'C'中,∠B= ∠B'(已证),∠ACB= ∠ A'C'B'(已知),AC= A'C'(已知),∴Rt△ABC≌Rt △A'B'C'().
例5 如图,在Rt△ABC和Rt △A'B'C'中,∠ACB=∠A'C'B'=90°,AB= A'B',AC= A'C',求证: Rt△ABC≌Rt △A'B'C'.
证明:由于直角边AC= A'C',我们移动Rt△ABC使点A与点A'重合,点C和点C'重合,且使点B和点B'分别位于A'C'两侧.
这样我们就证明了前面给出的H.L.判定定理
1.在△ABC中, 已知∠A=50°,∠B=65°,判断△ABC是什么三角形,为什么?
△ABC是等腰三角形, 因为∠B=65°, ∠A=50°, 所以∠C=65°, ∠B =∠C=65°,所以△ABC是等腰三角形.
2.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠1=_____,∠2=_____,图中的等腰三角形有___________________________.
3.已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm.
4.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个 C. 6个 D. 7个
5.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
6.如图,A,O,D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
数学八年级上册2 等腰三角形的判定课文配套ppt课件: 这是一份数学八年级上册2 等腰三角形的判定课文配套ppt课件,文件包含2等腰三角形的判定pptx、习题133pptx、2等腰三角形的判定doc等3份课件配套教学资源,其中PPT共35页, 欢迎下载使用。
初中数学人教版八年级上册13.3.2 等边三角形课文ppt课件: 这是一份初中数学人教版八年级上册13.3.2 等边三角形课文ppt课件,共10页。PPT课件主要包含了你能证明吗,等腰三角形的判定,求证ABAC,自己试一试,我来总结等内容,欢迎下载使用。
数学八年级上册11.2 实数教学演示课件ppt: 这是一份数学八年级上册11.2 实数教学演示课件ppt,共21页。













