





数学2.11 有理数的乘方教学课件ppt
展开2.如图,一正方体的棱长为a厘米, 则它的体积为________立方厘米.
1.如图,边长为a厘米的正方形的面积为______平方厘米.
读作:a的平方(或a的2次方)
读作:a的立方(或a的3次方)
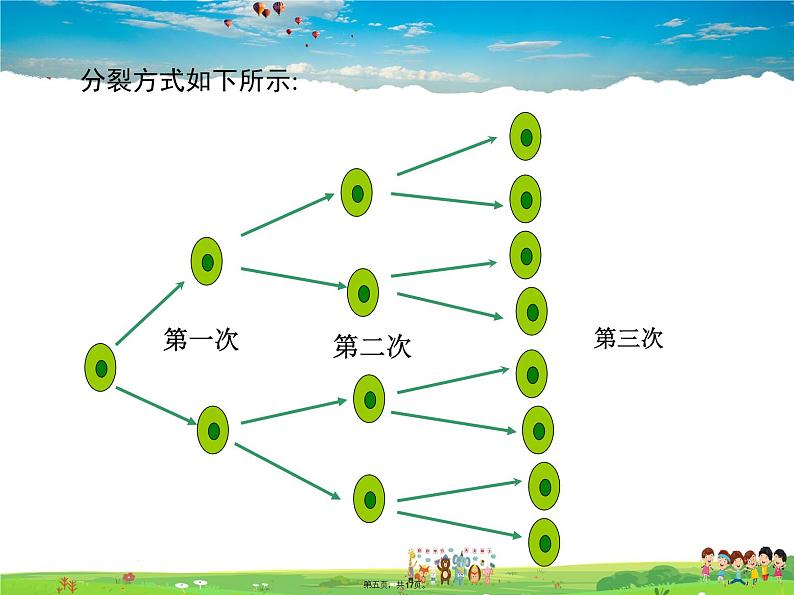
问题 某种细胞每30分钟便由一个分裂成两个.经过3小时这种细胞由1个能分裂成多少个?
这个细胞分裂一次可得多少个细胞?
那么,3小时共分裂了多少次?有多少个细胞?
解:一次得: 两次 : 三次 : 四次 :
六次 : 2×2×2×2×2×2个.
问题 这两个式子有什么相同点?
它们都是乘法;并且它们各自的因数都相同.
思考 同学们想一想:这样的运算能像平方、立方那样简写吗?
请比较细胞分裂四次后的个数式子:2×2×2×2和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
这样的运算我们可以像平方和立方那样简写:
乘方:求几个相同因数的积的运算,叫做乘方.
2×2×2×2×2×2
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方,例如8就是81,指数1通常省略不写.
例如,23中,底数是2,指数是3读作2的3次方,或2的3次幂.
23和32一样吗?为什么?
(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.(2) 表示_____个 相乘,读作 的____次方,也读作 的 次幂,其中 叫作 ,6叫作 .
注意:幂的底数是分数或负数时,底数应该添上括号!
例 计算:(1)(-2)3; (2)(-2)4; (3)(-2)5.
解:(1)(-2)3=(-2)(-2)(-2)=-8; (2)(-2)4=(-2)(-2)(-2)(-2)=16; (3)(-2)5=(-2)(-2)(-2)(-2)(-2)=-32.
思考 (-2)3与-23的意义是否相同?(-2)4与-24呢?
你发现正负数次幂有什么规律吗?
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何正整数次幂都是正数.
根据有理数的乘法法则可以得出:
0的任何正整数次幂都是0.
拓展:根据任何数与零相乘,都得零.可以得出:
(1)-(-3)2= ; (2)-32= ;
(3)(-5)3= ; 3= ;
(5)(-1)9= ; (6)(-1)12= ;
(7)(-1)n= .
(当n为奇数时)(当n为偶数时)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
1.求几个相同因数的积的运算,叫做乘方.
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正数次幂都是零.
初中数学2.11 有理数的乘方背景图课件ppt: 这是一份初中数学2.11 有理数的乘方背景图课件ppt,共12页。PPT课件主要包含了知识点,有理数乘方的意义,的10次方,a的n次方,以an为例,特别提醒,有理数的乘方运算等内容,欢迎下载使用。
华师大版七年级上册2.11 有理数的乘方课文内容课件ppt: 这是一份华师大版七年级上册2.11 有理数的乘方课文内容课件ppt,文件包含211有理数的乘方pptx、习题211pptx、211有理数的乘方doc等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
华师大版七年级上册2.11 有理数的乘方完整版ppt课件: 这是一份华师大版七年级上册2.11 有理数的乘方完整版ppt课件,文件包含211有理数的乘方课件pptx、习题211课件pptx等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。













