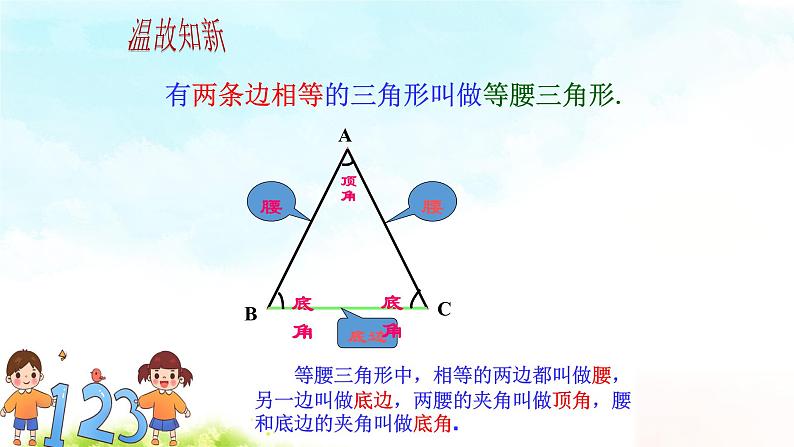
初中数学13.3.1 等腰三角形课文内容ppt课件

教

学

目

标

知识

技能

1.掌握等腰三角形的性质.

2.能运用性质进行相关计算与证明.

过程

方法

1.借助对称轴图形的性质，培养学生通过已学知识，发现新知识的能力；

2.提高学生几何符号语言能力.

情感

态度

通过轴对称探究等腰三角形的性质，体验数学充满着创造和乐趣，增强学好数学知识的自信心.

重点

等腰三角形的性质及应用.

难点

等腰三角形性质的证明.

环节

导 学 问 题

师 生 活 动

二次备课

情

境

引

入

【活动1】复习引入，进一步认识等腰三角形

问题1等腰三角形的有关概念你还记得那些内容？

等腰三角形

符号语言：△ABC中，AB=AC．

教师提出问题1，学生思考并回答问题．教师板书：△ABC中，AB=AC．并追问：如果只说等腰三角形ABC，会怎样？明确等腰三角形要指出哪条边是腰．

自

主

探

究

合

作

交

流

自

主

探

究

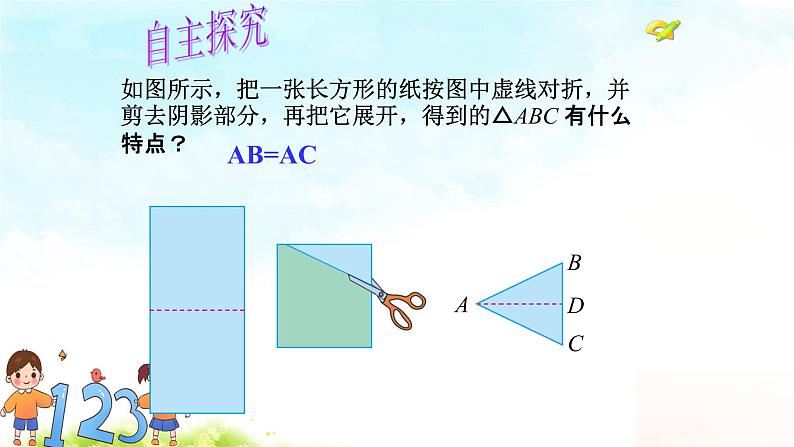
合

作

交

流

【活动2】探索等腰三角形的性质

问题2：你能用一张纸剪出等腰三角形吗？

追问：（1）观察剪出的是一个什么样的三角形？

     （2）仔细观察自己剪出的等腰三角形纸片，你能发现这个等腰三角形两个底角有什么数量关系？

     （3）我们可不可以说等腰三角形的两个底角相等？

     （4）用我们学过的知识给予证明.

     （5）这句话的已知是什么，结论是什么？

猜想：等腰三角形两个底角相等．

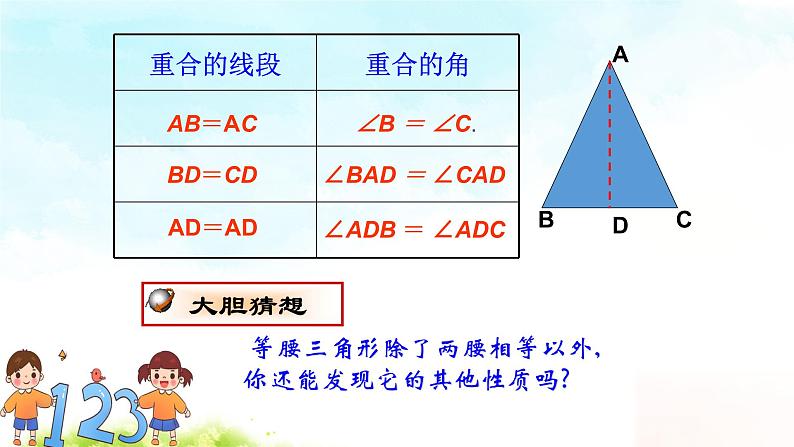
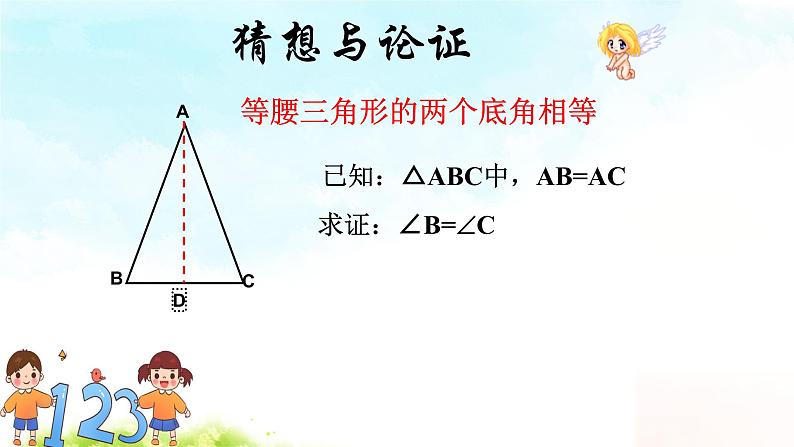
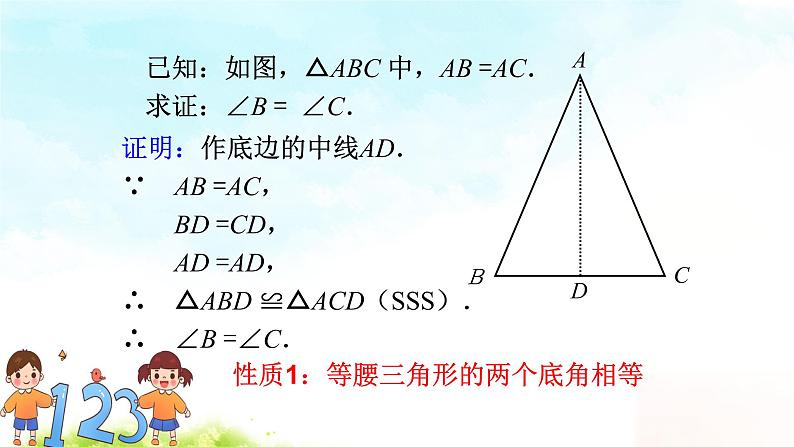
【活动3】证明等腰三角形性质

已知：如图，△ABC 中，AB =AC．

求证：∠B =∠C．

追问：1、如何证明两个角等？

      2、如何构造两个全等的三角形呢？

      3、刚刚折纸给你什么启示？

证明：作底边的中线AD．

　∴BD=BC

在△ABD 和△ACD中

AB =AC，

∵　BD =CD，

　　AD =AD，

∴　△ABD ≌△ACD（SSS）．

∴　∠B =∠C（全等三角形对应角相等）．

追问：还有没有其他证明方法

性质1：等腰三角形两个底角相等．（简写成“等边对等角”）

符号语言：∵△ABC 中，AB =AC

∴∠B =∠C

【活动4】再看自己剪好的等腰三角形，重点看折痕，你有新的发现？

性质2：等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合．（简写成“三线合一”）

在△ABC中

（1）∵AB=AC，AD⊥BC，

     ∴∠___=∠___，____=____；

（2）∵AB=AC，AD是中线，

     ∴∠＿=∠＿，____⊥____；

（3）∵AB=AC，AD是角平分线，

     ∴____⊥____，____=____.

 [例1]如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，

求：△ABC各角的度数．

   分析：根据等边对等角的性质，我们可以得到∠A=∠ABD，∠ABC=∠C=∠BDC，

再由∠BDC=∠A+∠ABD，就可得到∠ABC=∠C=∠BDC=2∠A．

再由三角形内角和为180°，就可求出△ABC的三个内角．

   把∠A设为x的话，那么∠ABC、∠C都可以用x来表示，这样过程就更简捷．

      解：因为AB=AC，BD=BC=AD，

    所以∠ABC=∠C=∠BDC．

    ∠A=∠ABD（等边对等角）．

设∠A=x，

则  ∠BDC=∠A+∠ABD=2x，

    从而∠ABC=∠C=∠BDC=2x．

    于是在△ABC中，有

    ∠A+∠ABC+∠C=x+2x+2x=180°，

解得x=36°．  

 在△ABC中，∠A=35°，

∠ABC=∠C=72°

学生展示自己的剪裁结果．

学生独立思考后尝试着概括等腰三角形的性质1.

教师问：要证两个角相等你有什么办法？教师关注学生：

（1）是否想到用全等

（2）如何添加辅助线

给学生足够的时间思考，并独立完成证明，学生板书，白板投影其他证明方法．

猜想成立，即得出等腰三角形性质1.

教师引导学生得到性质2，并强调性质2的应用很重要，我们要在下节课中重点研究性质2．

教师重点启发这个性质可以用类似的方法证明，等腰三角形顶角的平分线平分底边并且垂直于底边，底边上的高平分顶角平分底边，这也就证明了性质2.

ppt展示符号语言.

教师出示例1，引导学生分析，由已知线段相等可以得到哪些角相等？

学生先自主探究，然后合作交流，最后展示；师生共同评价

尝

试

应

用

⒈等腰三角形一个底角为75°,它的另外两个角为____        ；

⒉等腰三角形一个角为70°,它的另外两个角为___________________；

⒊等腰三角形一个角为110°,它的另外两个角为_______。

4、如图，AB=AC，∠A=40°，AB的垂直平分线交AC于D，则∠DBD的度数为        。

5、如图，△ABC是等腰直角三角形（AB=AC,∠BAC=90°）,AD是底边BC上的高，写出∠B,∠C,∠BAD,∠DAC的度数，并写出图中有哪些相等的线段？

教师出示问题，学生自主、合作、展示，师生共同评价

1、75°, 30°

2、70°,40°或55°,55°

3、35°,35°

4、30°

5、解：∠B＝∠C＝∠BAD＝∠DAC＝45°

图中相等的线段有:

AB=AC,AD=BD=CD.

成

果

展

示

本节课你学到了什么？

等腰三角形的三条性质；

你还有什么疑惑？

教师引导学生总结本节所学知识，所掌握的方法，注意点拨、诱导、强调

补

偿

提

高

6、如图，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数

6、解：∵AB=AD=DC

∴ ∠B= ∠ADB，∠C= ∠DAC

设 ∠C=x，则 ∠DAC=x，

∠B= ∠ADB= ∠C+ ∠DAC=2x

在△ABC中，

∠B+ ∠C+ ∠BAD+ ∠DAC

=2x+x+26°+x=180°

解得：x=38.5°，

∴ ∠B=77°， ∠C= 38.5°

作

业

设

计

作业：教材77页第3题

同步56页9、11题

学生认定作业，课下独立完成